Licence 1 > Electrocinétique > Cours 1 : Lois dans l'approximation des régimes quasi stationnaires
EC1 : Lois dans l'approximation des régimes quasi stationnaires
Une grosse partie de ce chapitre est disponible en vidéos, la première de la playlist est ici :Si vous souhaitez avoir accès à une notion particulière les séquences individuelles sont ici :
- Intensité et tension, vocabulaire, loi des mailles et loi des noeuds
- Puissance, conducteurs ohmiques et associations, diviseurs de tension et de courant, dipôle actif ou passif
- Condensateurs, bobines et générateurs réels
Introduction
Ce chapitre sera l’occasion de définir les bases de l’électrocinétique, de revoir les grandeurs physiques comme la tension et le courant, ainsi que les lois qui les concernent dans un circuit quelconque.
Qu’est-ce que l’électrocinétique ?
L’électrocinétique est l’étude du mouvement d’ensemble des porteurs de charge dans un circuit que l’on appelle courant électrique. Les charges se déplacent sous l’effet d’un champ électrique extérieur.
Rappels sur les grandeurs intensité et tension
Intensité du courant
Sens conventionnel
On a attribué un sens conventionnel au courant électrique qu’il convient de respecter : le courant électrique est compté positivement lorsqu’il va dans le même sens que celui dans lequel se déplaceraient des charges positives soumis à un champ extérieur.
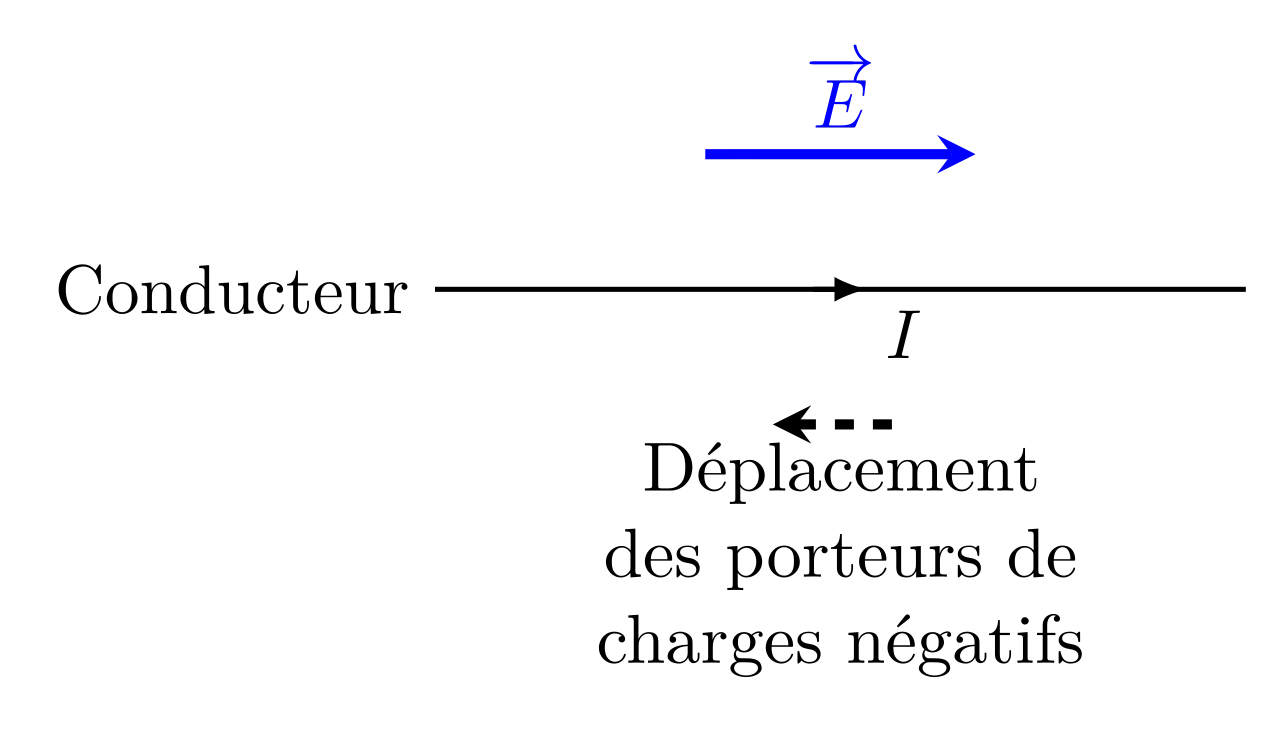
Définition
Comme nous l’avons déjà vu, l’intensité du courant est la quantité de charges \(\delta q\) qui traverse une section \(S\) du conducteur pendant un temps \(\delta t\). Son unité est l’ampère (A), 1A correspond à \(1\,\mathrm{C.s^{-1}}\).
Tension
Définition et mesure
La tension est une différence de potentiel électrique entre deux points d’un circuit et se mesure avec un voltmètre qui la donne en Volt (V).
Il n’existe pas d’appareil pour mesurer le potentiel électrique en un point, on ne fait que mesurer des différence de potentiels : pour cela, on fixe arbitrairement le point de potentiel nul appelé la masse.
Comme on l’a vu en électrostatique, le potentiel électrique n’est défini qu’à une constante près.
Convention
Comme pour l’intensité du courant, on choisit un sens conventionnel pour la tension : on note \(U_{AB} = V(A)-V(B)\) la tension entre les points A et B d’un circuit par une flèche dirigée de B vers A. \(U_{AB}\) est positive si \(V(A)>V(B)\).
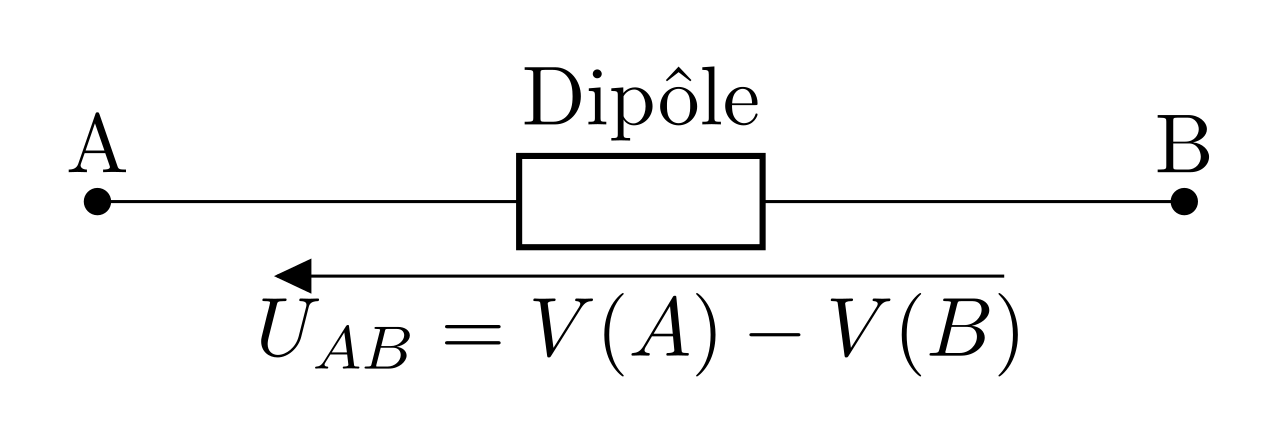
aux bornes d'un dipôle
Régimes continus ou variables, approximation des régimes quasi-stationnaires (ARQS)
Régimes continus ou variables
On parle de régime continu lorsque les grandeurs électriques, notamment l’intensité et la tension ne dépendent pas du temps.
On parle de régime variable si ces grandeurs varient dans le temps, ce qui peut avoir plusieurs causes : cas du régime transitoire de la charge ou décharge d’un condensateur, cas d’un régime forcé imposé par un GBF.
Approximation des régimes quasi-stationnaires (ARQS)
Définition
Cette approximation consiste à dire que quel que soit le régime, l’intensité du courant est la même en tout point d’une branche de circuit.
Validité
Cette approximation est valable pour un régime variable si le temps caractéristique de sa variation (\(\tau\) pour la charge ou décharge d’un condensateur, \(T\) pour un signal sinusoïdal imposé par un GBF) est grand devant le temps de propagation de l’intensité.
Cette approximation sera possible si les dimensions du circuit ne sont pas trop grandes, car l’intensité se propageant à une vitesse proche de celle de la lumière, le temps de propagation est \(\dfrac{L}{c}\) ce qui fait \(10^{-8}\mathrm{s}\) pour un circuit d’1 mètre de longueur.
Les régimes variables étudiés ont des temps caractéristiques bien plus grand (ex : régime transitoire de la décharge d’un condensateur de capacité \(1\,\mu \mathrm{F}\) dans une résistance de \(500\,\Omega\) : \(5\times\tau = 5\times RC = 2.5\,10^{-3}\,\mathrm{ms} >> 10^{-8}\mathrm{s}\)).
Dans tout ce qui suit, on considérera les conditions de l’ARQS réalisées.
Loi des nœuds et loi des mailles
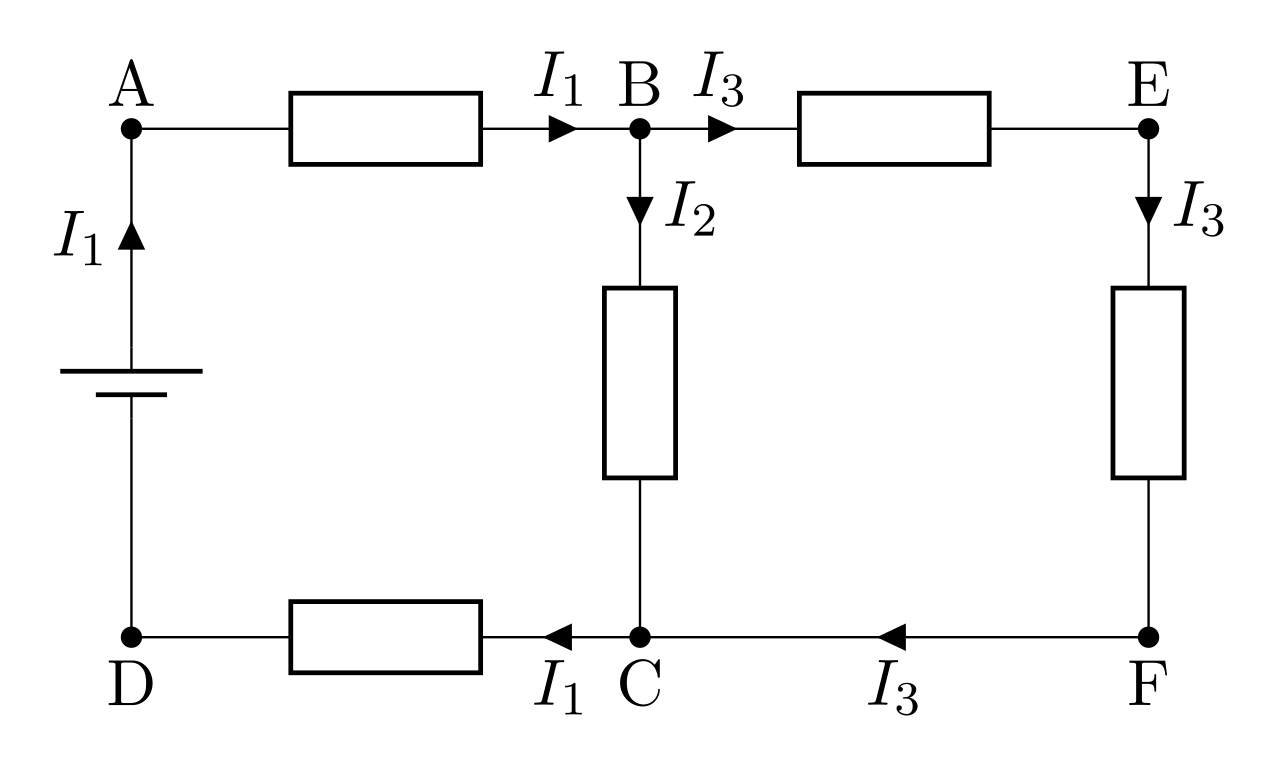
Avant d’écrire ces lois, définissons quelques notions relatives au circuit électrique :
Une branche est constituée d’une association en série d’un ou plusieurs dipôles (fils, résistance, bobine, ...) : dans le circuit ci-contre, AB est une branche, BC également, ...
Un nœud est un point du circuit où se retrouvent plusieurs branches : le nœud B réunit les branches AB, BC et BE.
Une maille est une série de branches qui part d’un nœud pour revenir au même nœud : on définit la maille ABCD ou BEFC ou AEFD ...
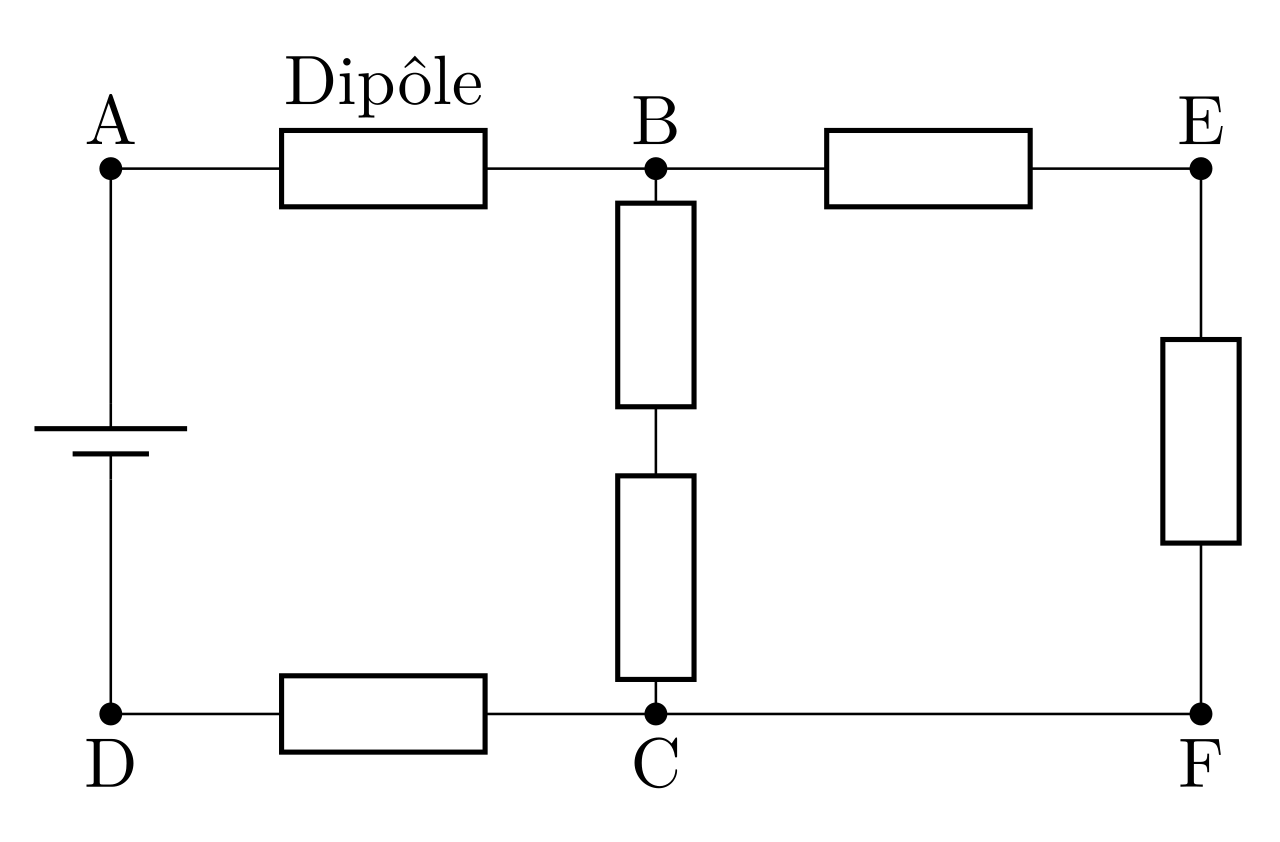
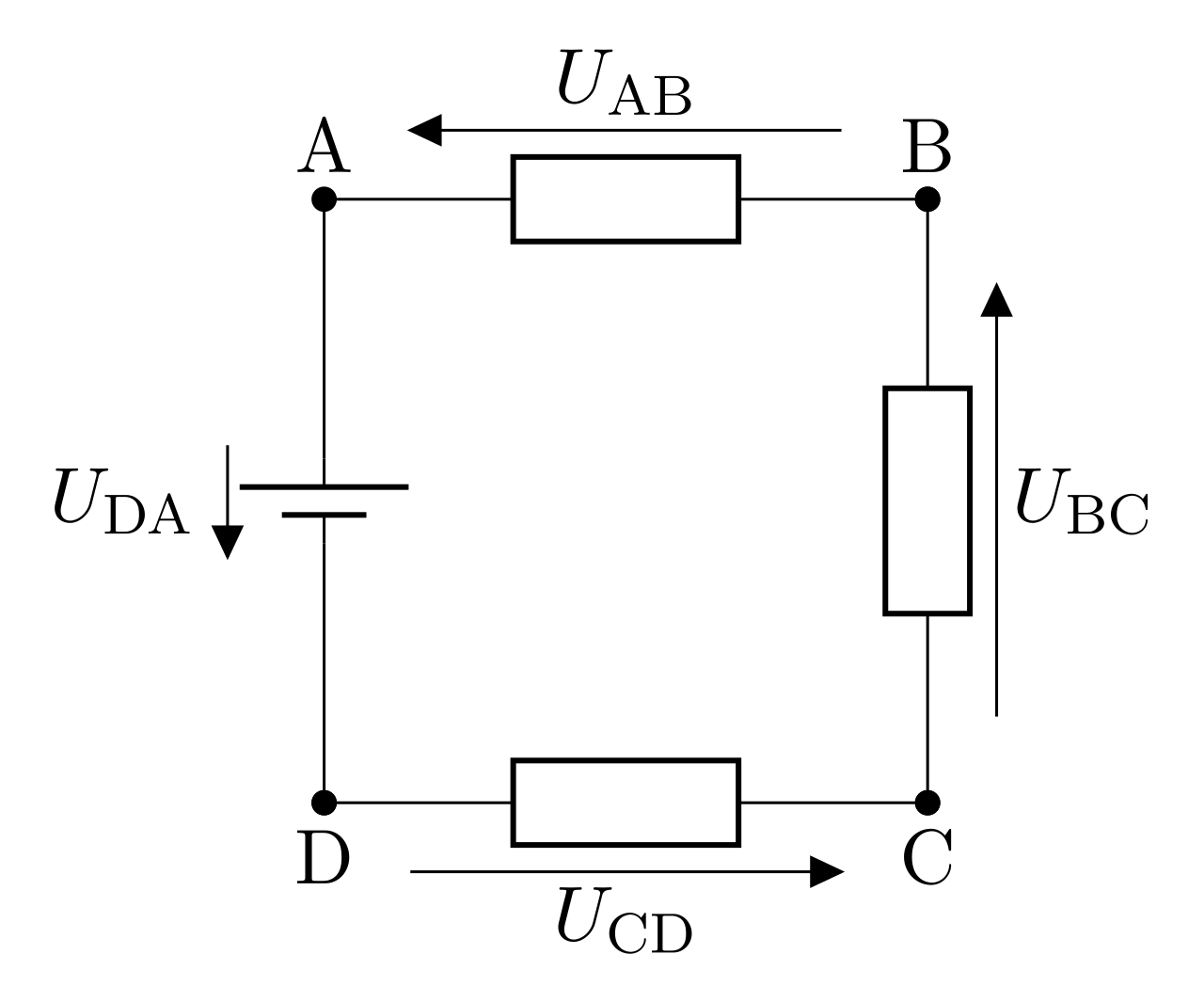
Loi des mailles
La somme des tensions à l’intérieur d’une maille est nulle.
Sur la maille ABCD, on a :
\begin{equation}\boxed{U_{AB} + U_{BC} + U_{CD} + U_{DA} = 0 }\end{equation}
En effet :
\begin{equation}V_A-V_B + V_B -V_C + V_C -V_D + V_D -V_A = 0\end{equation}
Loi des noeuds
Cette loi traduit la conservation de la charge électrique.
La somme des courants qui arrivent sur un nœud est égale à la somme des courants qui en repart :
\begin{equation}\boxed{I_1 = I_2 + I_3 }\end{equation}
Puissance reçue, conventions générateur et récepteur
Soit un dipôle dans la configuration ci-contre.
La puissance reçue par ce dipôle est définie par :
\begin{equation}\boxed{P=U\times I}\end{equation}
Cette puissance est positive dans le cas d’un dipôle récepteur.
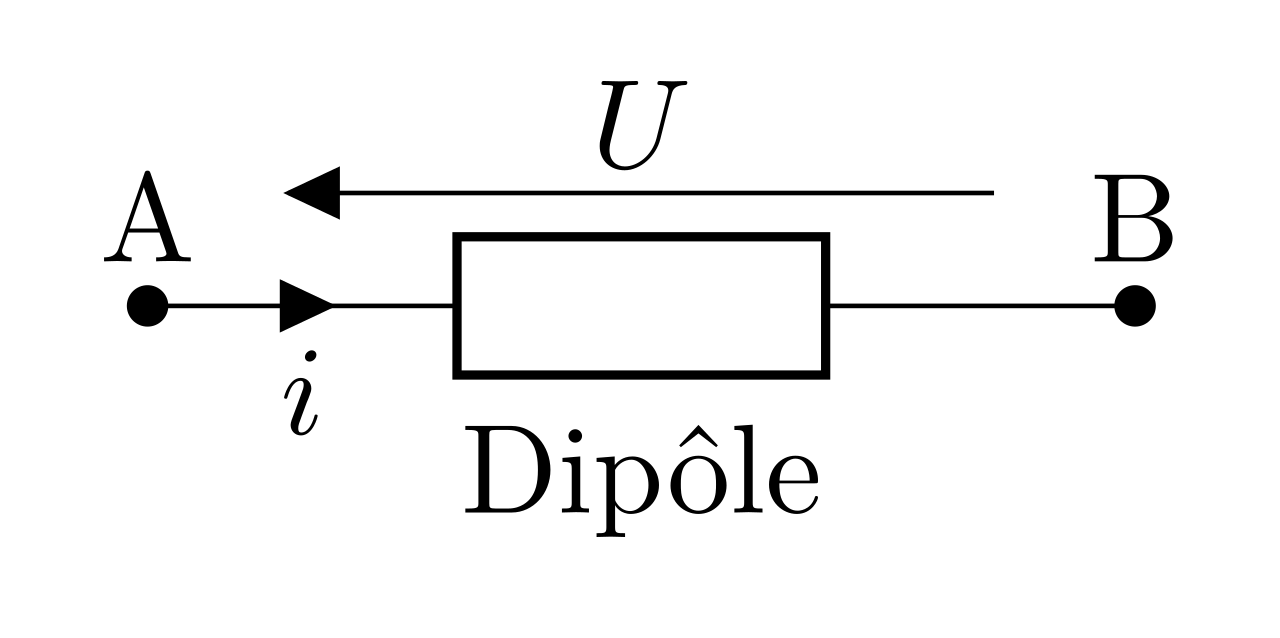
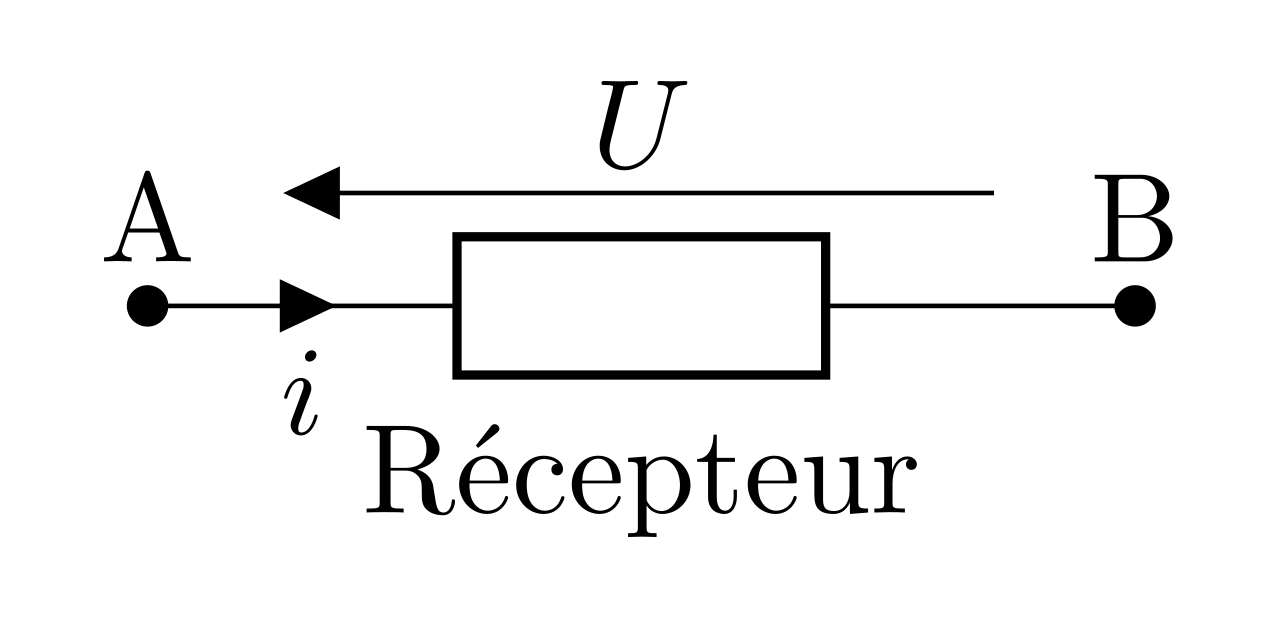
Ainsi, la configuration présentée ci-contre est appelée convention récepteur : les sens de I et U sont opposés.
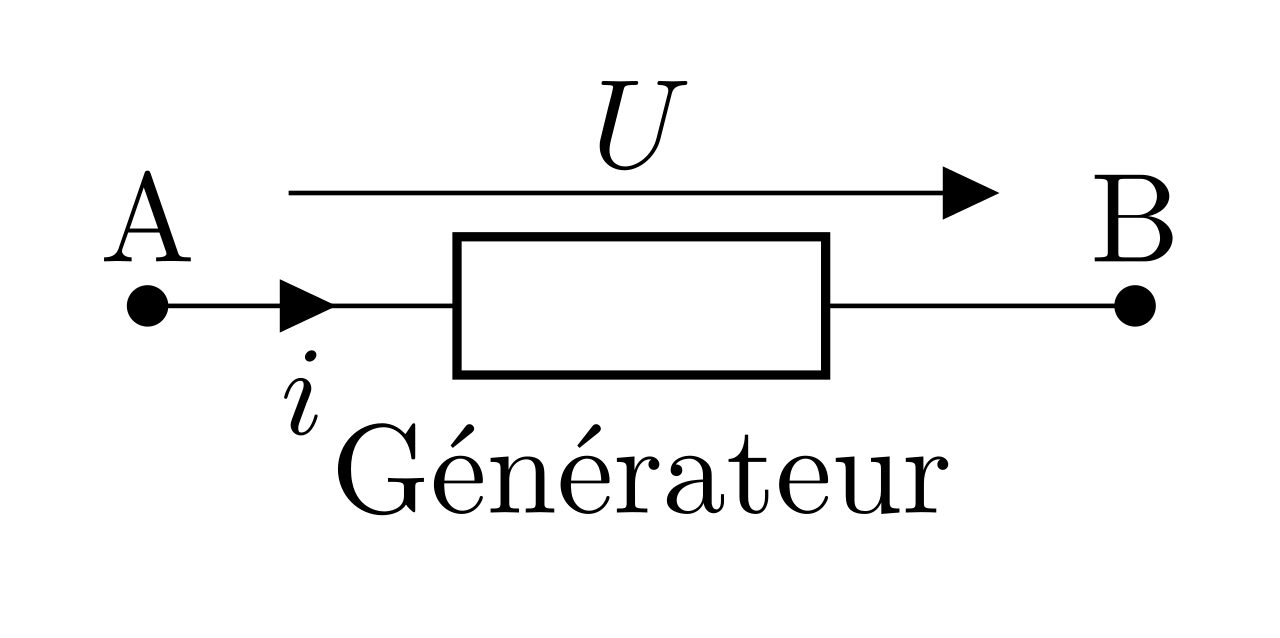
Alors, si la puissance reçue est négative, c’est que le dipôle fournit de l’énergie. C’est un générateur et on utilisera la convention générateur : I et U sont dans le même sens.
Caractéristique d’un dipôle
Lorsque l’on souhaite tracer la caractéristique d’un dipôle, on s’intéresse à la fonction u=f(i) (caractéristique tension-courant). Si cette fonction est une droite, on parle de dipôle linéaire.
Dipôle actif ou passif
Un dipôle passif
est un dipôle qui convertit toute l’énergie électrique qu’il reçoit en énergie thermique (conducteur ohmique, diode, ...).
Sa caractéristique passera forcément par l’origine.
Un dipôle actif
fournit à l’extérieur de l’énergie thermique et une autre forme d’énergie :
Un générateur fournira de l’énergie thermique et de l’énergie électrique ;
Un récepteur comme un moteur fournit de l’énergie thermique et de l’énergie mécanique à partir d’énergie électrique.
La caractéristique de ces dipôles ne passe pas par l’origine.
Les conducteurs ohmiques
Loi d’Ohm
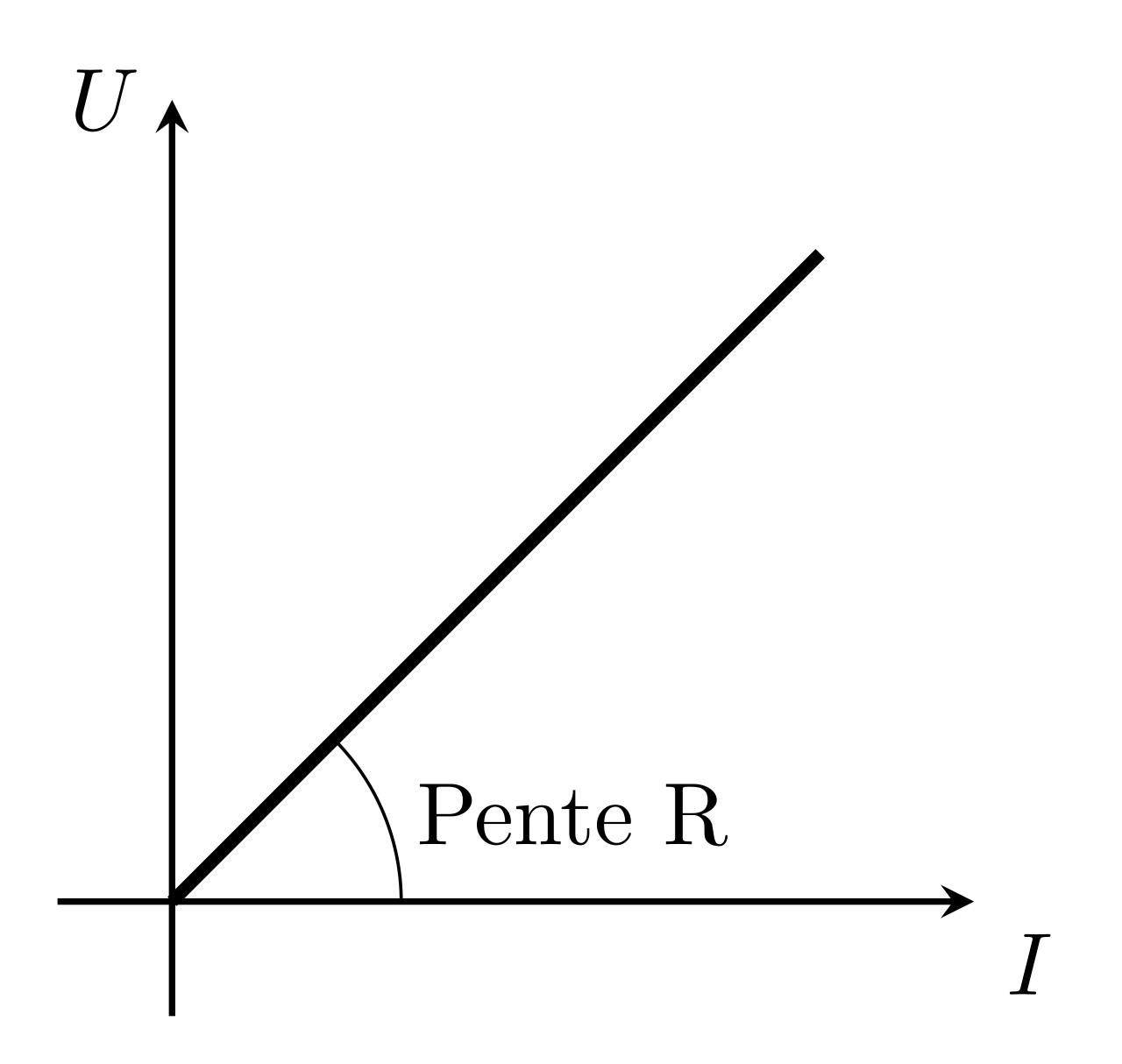
Un conducteur ohmique est un dipôle dont la caractéristique est une droite passant par l’origine. Il répond donc à la loi d’Ohm qui s’écrit :
\begin{equation}\boxed{U=R\,I}\end{equation}
Avec \(u\), la tension en Volt(V), \(i\), l’intensité en ampère (A) et \(R\) la résistance du conducteur ohmique exprimée en Ohm (\(\Omega\)).
Effet Joule
On appelle effet Joule la dissipation de l’énergie électrique reçue par énergie thermique dans un dipôle.
Le conducteur ohmique dissipe sous forme de chaleur la puissance :
\begin{equation}\boxed{P=R\,I^{2}}\end{equation}
Association de conducteurs ohmiques
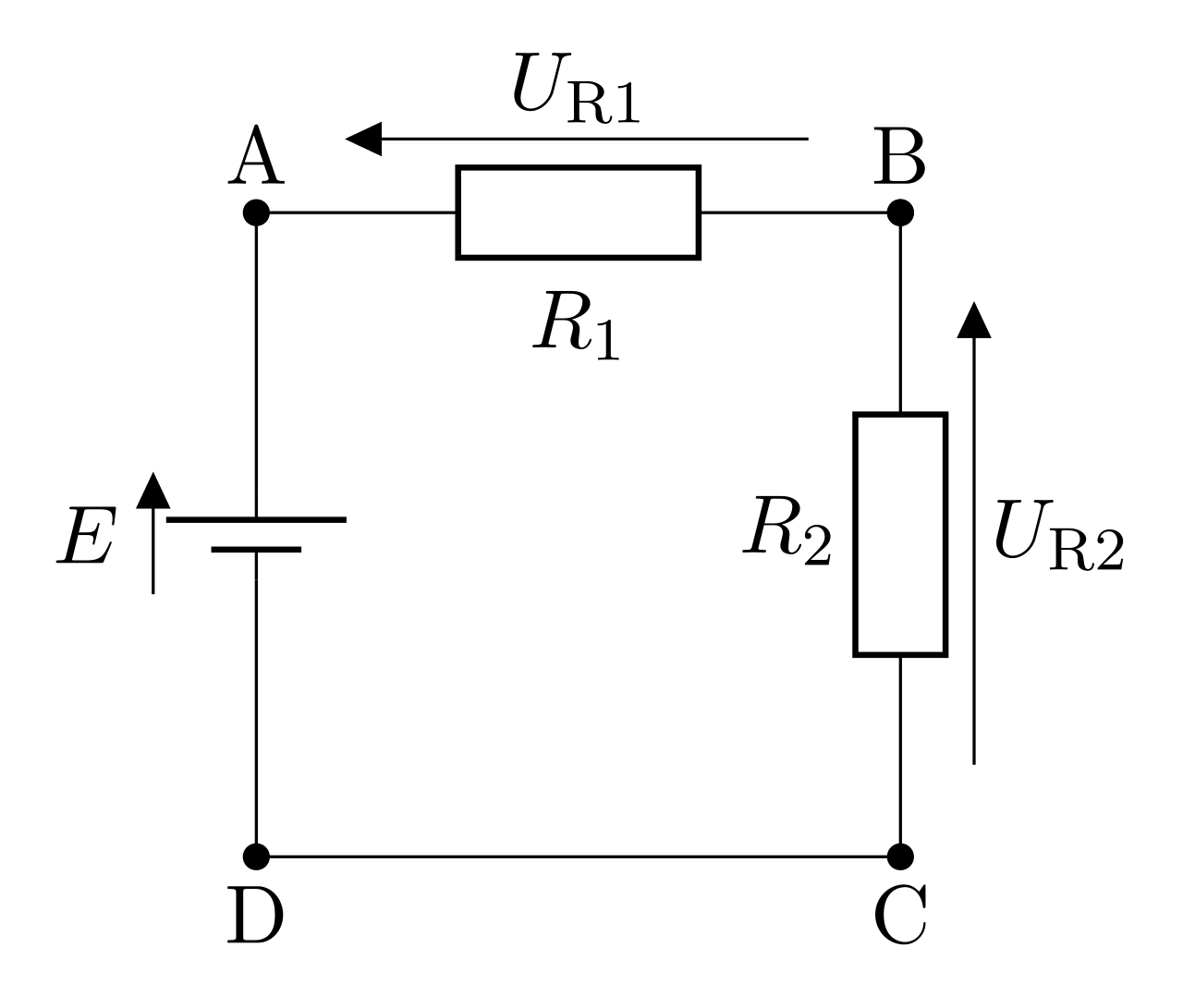
Association en série : montage diviseur de tension
Lorsque l’on associe plusieurs conducteurs ohmiques en série, leurs résistances s’ajoutent : La résistance globale est appelée "résistance équivalente".
Pour la situation ci-dessous, on a :
\begin{equation}R_{eq}=R_{1}+R_{2}+R_{3}\end{equation}

conducteurs ohmique en série
Dans cette association en série de conducteurs, on peut utiliser la propriété "diviseur de tension". Elle consiste à exprimer la tension aux bornes d’un conducteur en fonction de sa résistance, de la résistance équivalente et de la tension aux bornes de l’ensemble.
Voici un exemple :
\begin{equation}\boxed{U_{R_1} = \dfrac{R_1}{R_1+R_2}E = \dfrac{R_1}{R_{\mathrm{eq}}}E}\end{equation}
\begin{equation}\boxed{U_{R_2} = \dfrac{R_2}{R_1+R_2}E = \dfrac{R_2}{R_{\mathrm{eq}}}E}\end{equation}
\(U_{R_1}\) et \(U_{R_2}\) ne sont qu’une fraction de la tension \(E\), le montage s’appelle un diviseur de tension.
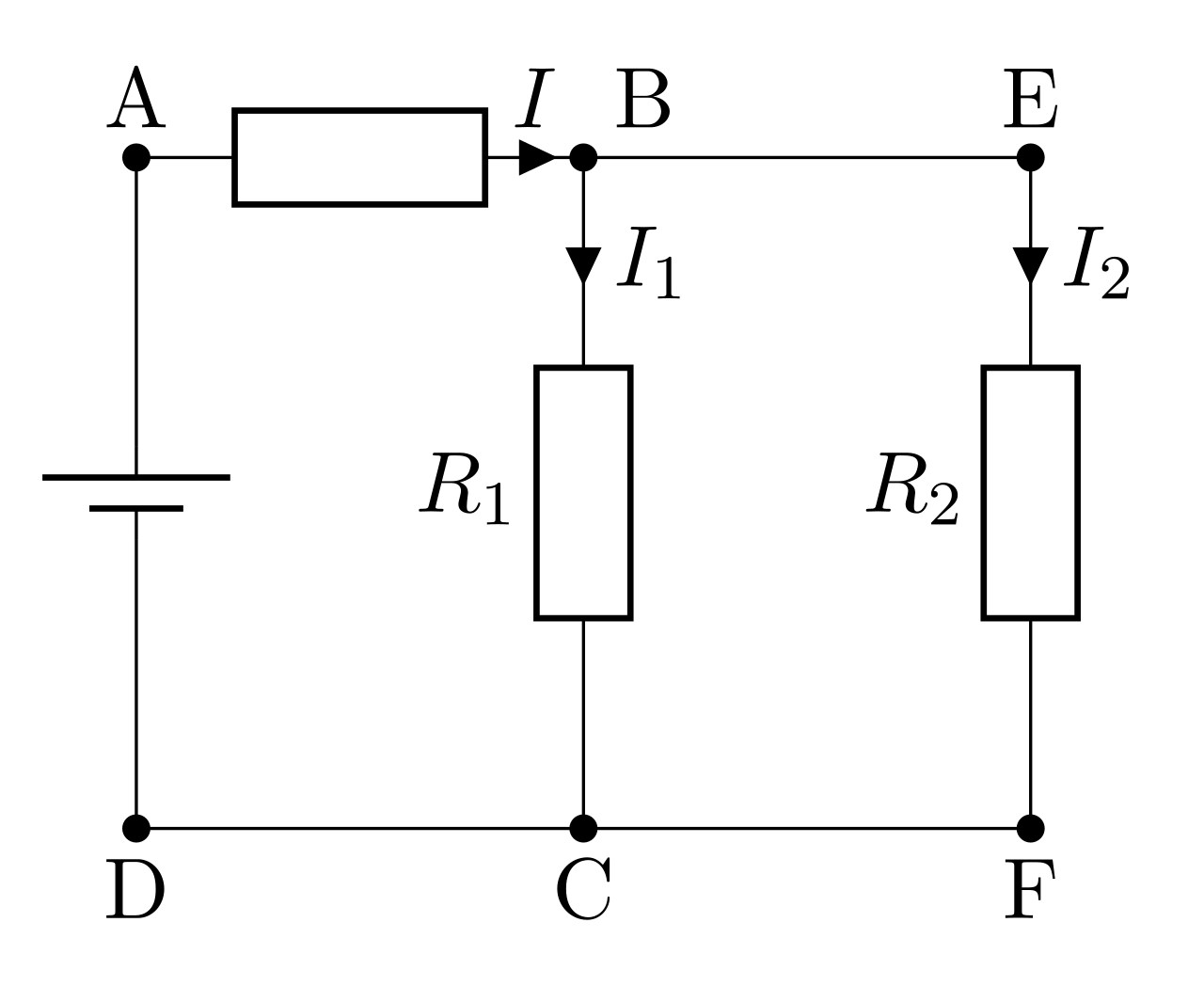
Association en parallèle : montage diviseur de courant
Lorsque l’on associe plusieurs conducteurs ohmiques en parallèle, leurs conductances définies par \(G=\dfrac{1}{R}\) s’ajoutent :
Pour la situation ci-dessous, on a :
\begin{equation}\boxed{\dfrac{1}{R_{\mathrm{eq}}}= \dfrac{1}{R_{1}} + \dfrac{1}{R_{2}} + \dfrac{1}{R_{3}}}\end{equation}
\begin{equation}\boxed{G_{\mathrm{eq}}= G_{1} + G_{2} + G_{3}}\end{equation}

conducteurs ohmique en dérivation
Dans cette configuration en parallèle, on peut utiliser le diviseur de courant :
\begin{equation}\boxed{I_1 = \dfrac{G_1}{G_1+G_2}I = \dfrac{G_1}{G_{\mathrm{eq}}}I=\dfrac{R_2}{R_1+R_2}I}\end{equation}
En effet, pour deux résistances en parallèle, on a \(R_{\mathrm{eq}}=\dfrac{1}{G_{\mathrm{eq}}}=\dfrac{R_1R_2}{R_1+R_2}\), donc :
\begin{equation}I_1 =\dfrac{G_1}{G_{\mathrm{eq}}}I = \dfrac{1}{R_1} \dfrac{R_1R_2}{R_1+R_2} = \dfrac{R_2}{R_1+R_2}I\end{equation}
\(I_1\) n’est qu’une fraction de l’intensité \(I\), le montage s’appelle un diviseur de courant.
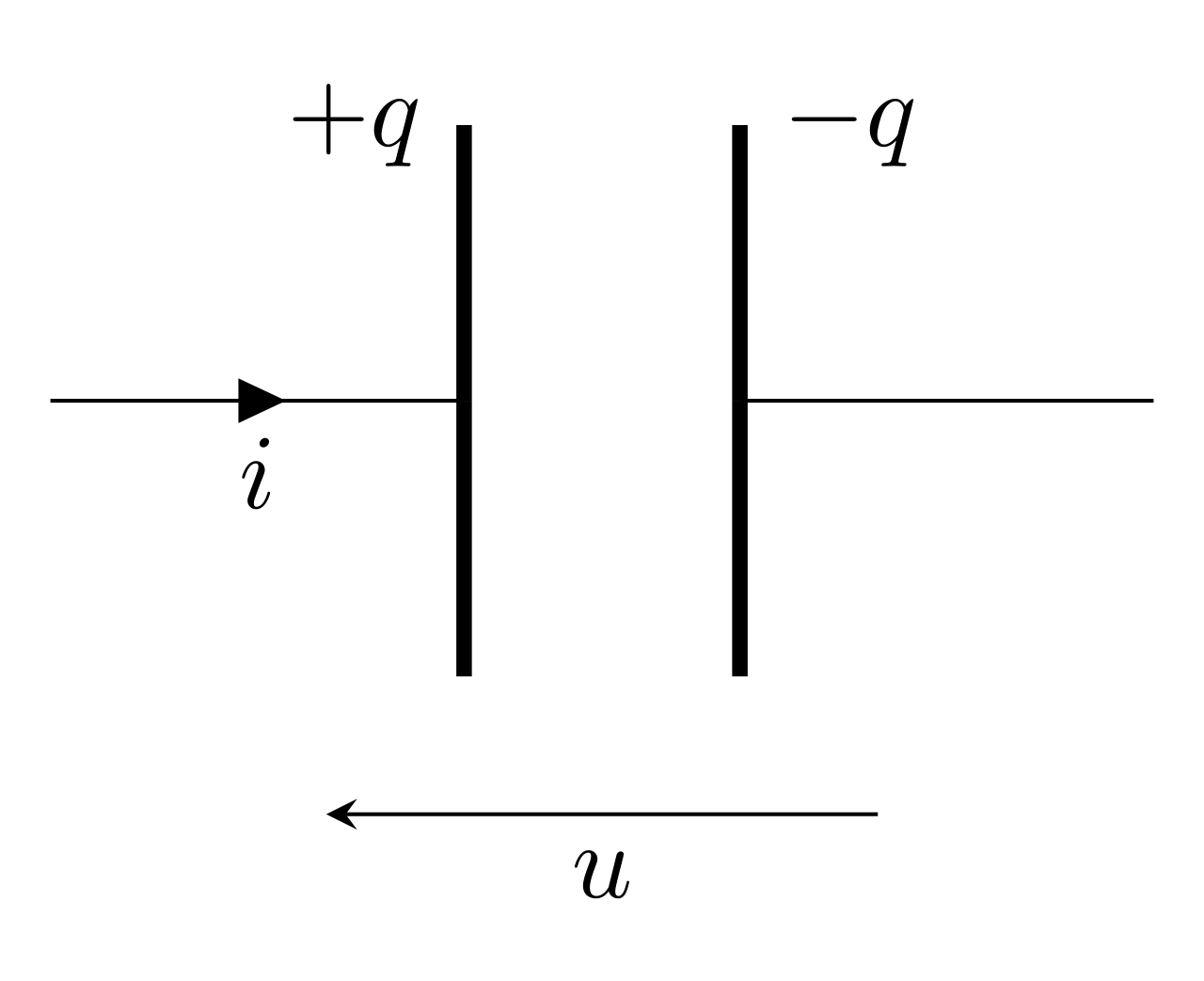
Le condensateur
Constitution et symbole
Un condensateur est constitué de deux armatures conductrices séparées par un isolant appelé diélectrique.
Ils peuvent être plans, cylindriques voir sphériques.
Les condensateurs sont caractérisés par leur capacité \(C\) qui s’exprime en Farad. C’est la capacité qu’ils ont à accumuler des charges lorsqu’ils sont soumis à une certaine différence de potentiel.
L’armature qui reçoit le courant porte la charge \(+q\), l’autre porte la charge \(-q\).
On symbolisera ainsi le condensateur de la manière suivante :
Relation tension-intensité
On connaît la relation entre la charge portée par l’armature positive et la tension appliquée aux bornes du condensateur :
\begin{equation}q = C\,u\end{equation}
On connaît la relation entre l’intensité du courant arrivant sur le condensateur et la variation de charge de l’armature positive :
\begin{equation}i=\dfrac{\mathrm{d}q}{\mathrm{d}t}\end{equation}
D’où :
\begin{equation}\boxed{i=C\dfrac{\mathrm{d}u}{\mathrm{d}t}}\end{equation}
Comportement du condensateur sous différents régimes
Le condensateur n’est "intéressant" qu’en régime variable, c’est à dire lorsque \(u\) varie.
En effet, en régime permanent, la tension étant constante, on a :
\begin{equation}i=C\dfrac{\mathrm{d}u}{\mathrm{d}t} = 0\end{equation}
Le condensateur se comporte donc en régime permanent comme un interrupteur ouvert.
Énergie emmagasinée par le condensateur
L’énergie emmagasinée par le condensateur entre le temps \(t=0\) où \(u=0\) et le temps \(t\) où \(u=u\) est donnée par :
\begin{equation}\boxed{E_C = \dfrac{1}{2}\,C\,u^2}\end{equation}
Attention, la puissance reçue par un condensateur peut changer de signe au cours du temps :
Si son énergie \(E_C\) augmente, la puissance reçue (\(P=u(t)\,i(t)\)) est positive est le condensateur se comporte comme un récepteur.
Si son énergie \(E_C\) diminue, la puissance reçue est négative est le condensateur se comporte comme un générateur.
Conséquence sur la continuité de la fonction \(u(t)\)
L’énergie emmagasinée par un condensateur dépend de la tension à ses bornes. Ce transfert d’énergie ne pouvant pas se faire instantanément, la tension \(u(t)\) aux bornes d’un condensateur est une fonction continue du temps.
Association de condensateur
Association en série
Trois condensateurs de capacité C\(_1\), C\(_2\), C\(_3\) placés en série sont équivalents à un condensateur de capacité C\(_{eq}\) vérifiant la relation suivante :
\begin{equation}\boxed{\dfrac{1}{C_{\mathrm{eq}}} = \dfrac{1}{C_1} + \dfrac{1}{C_2} + \dfrac{1}{C_3}}\end{equation}
Association en parallèle
Trois condensateurs de capacité C\(_1\), C\(_2\), C\(_3\) placés en parallèles sont équivalents à un condensateur de capacité C\(_{eq}\) vérifiant la relation suivante :
\begin{equation}\boxed{C_{\mathrm{eq}} = C_1 + C_2 + C_3}\end{equation}
La bobine
Constitution et symbole
Une bobine est constituée d’un enroulement de spires conductrices autour d’un isolant. Elle admet donc une certaine résistance interne du fait de cette grande longueur de fil.
La bobine sera donc symbolisée en convention récepteur de la manière suivante :

Relation tension-intensité
Le phénomène qui caractérise la bobine est l’auto-induction : le passage d’un courant \(i\) qui varie dans les spires de la bobine créé un champ magnétique \(\overrightarrow{B}\) qui fait apparaître une tension \(u\) aux bornes de celle-ci (phénomène vu plus précisément en 2ème année).
Mathématiquement, pour une bobine idéale (sans résistance interne), cette auto-induction s’écrit :
\begin{equation}\boxed{u = L\dfrac{\mathrm{d}i}{\mathrm{d}t}}\end{equation}
où L est l’inductance de la bobine qui s’exprime en Henry (H).
En tenant compte de la résistance interne de la bobine, la tension aux bornes de celle-ci s’écrit :
\begin{equation}\boxed{u = L\dfrac{\mathrm{d}i}{\mathrm{d}t} + r\,i}\end{equation}
avec \(r\) la résistance interne de la bobine qui s’exprime en Ohm (\(\Omega\)).
Comportement de la bobine sous différents régimes
La bobine n’est "intéressante" qu’en régime variable, c’est à dire lorsque \(i\) varie.
En effet, en régime permanent, l’intensité étant constante, on a :
\begin{equation}u = L\dfrac{di}{dt} + r\,i = r\,i\end{equation}
La bobine se comporte donc en régime permanent comme un conducteur ohmique de faible résistance (\(r=10-12\,\Omega\)).
Énergie emmagasinée par la bobine
Pour une bobine idéale, l’énergie emmagasinée par celle-ci entre le temps \(t=0\) où \(i=0\) et le temps \(t\) où \(i=i\) est donnée par :
\begin{equation}\boxed{E_L = \dfrac{1}{2}\,L\,i^2}\end{equation}
Attention, la puissance reçue par une bobine peut changer de signe au cours du temps :
Si son énergie E augmente, la puissance reçue (\(P=u(t)\,i(t)\)) est positive est la bobine se comporte comme un récepteur.
Si son énergie E diminue, la puissance reçue est négative est la bobine se comporte comme un générateur.
Pour une bobine réelle, pendant qu’elle emmagasine l’énergie \(E_L\), elle en dissipe aussi par effet Joule.
Conséquence sur la continuité de la fonction \(i(t)\)
L’énergie emmagasinée par une bobine dépend de l’intensité du courant qui la traverse. Ce transfert d’énergie ne pouvant pas se faire instantanément, l’intensité du courant \(i(t)\) parcourant une bobine est une fonction continue du temps.
Association de bobines
Les lois d’association en série et en parallèle des bobines sont les mêmes que celles pour les conducteurs ohmiques.
Association en série
On peut considérer le cas des bobines réelles :
Une association de \(n\) bobines réelles identiques caractérisées par le couple \(L,r\) est équivalente à une bobine d’inductance \(nL\) associée à un conducteur ohmique de résistance \(n\,r\).
Association en parallèle
La modélisation en parallèle de bobines réelles n’étant pas aisée, on s’occupe de bobines idéales :
Soit deux bobines idéales d’inductances \(L_1\) et \(L_2\) placées en parallèle, cette association est équivalente à une bobine d’inductance \(L_{\mathrm{eq}}\) qui vérifie :
\begin{equation}\boxed{\dfrac{1}{L_{\mathrm{eq}}}=\dfrac{1}{L_1}+\dfrac{1}{L_2} }\end{equation}
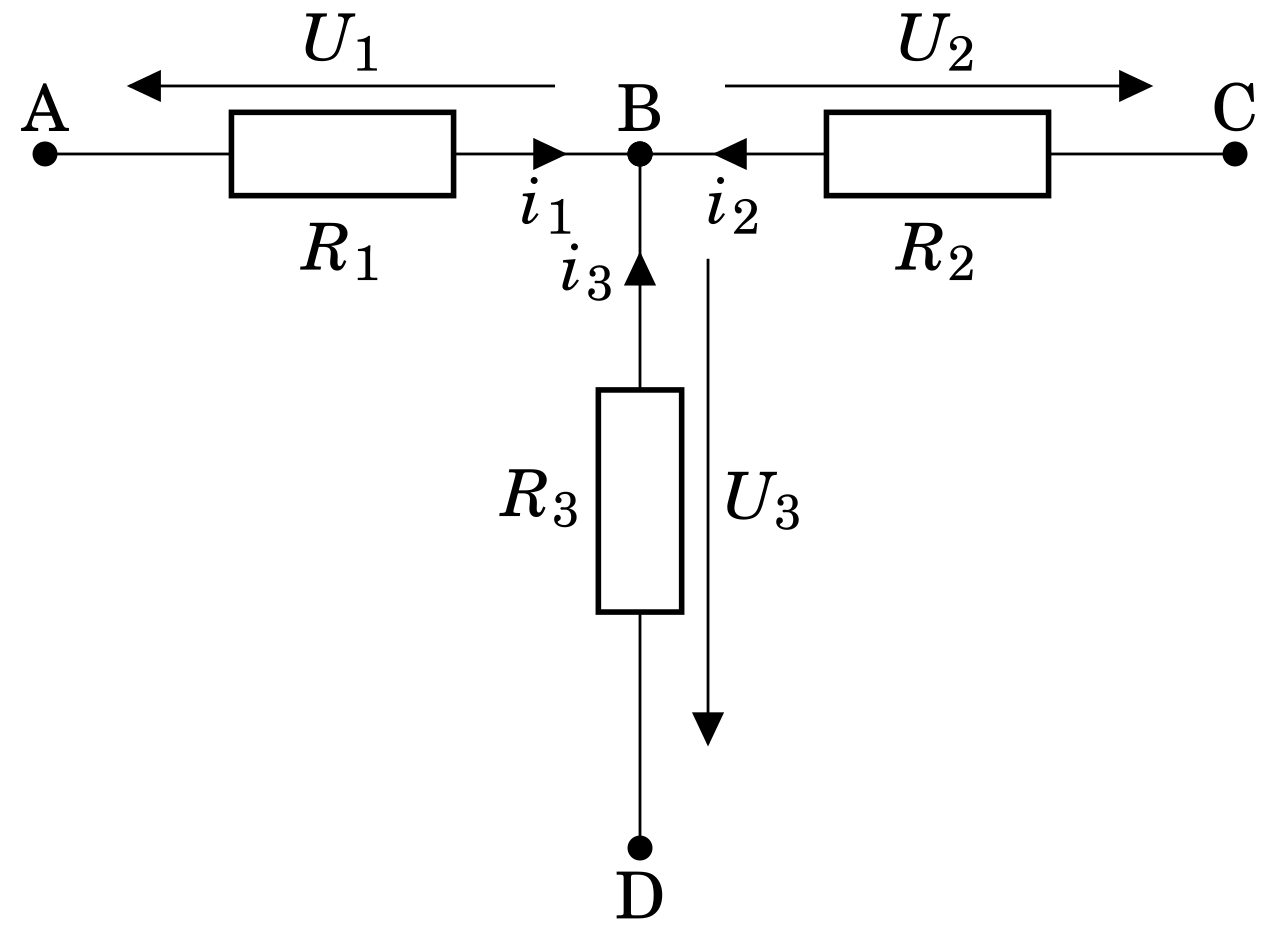
Théorème de Millman
Ce théorème exprime la loi des noeuds en terme de potentiels électriques :
Si on applique la loi d’Ohm à chaque dipôle, on a :
\begin{equation}\begin{aligned} I_1 = \dfrac{U_1}{R_1}=\dfrac{V_A-V_B}{R_1} \\ I_2 = \dfrac{U_2}{R_2}=\dfrac{V_C-V_B}{R_2} \\ I_3 = \dfrac{U_3}{R_3}=\dfrac{V_D-V_B}{R_3}\end{aligned}\end{equation}
On applique ensuite la loi des noeuds :
\begin{equation}\begin{aligned} & I_1 + I_2 + I_3 = 0 \\ \Longleftrightarrow & \dfrac{V_A-V_B}{R_1} + \dfrac{V_C-V_B}{R_2} + \dfrac{V_D-V_B}{R_3} = 0\end{aligned}\end{equation}
Et le théorème de Millman s’écrit :
\begin{equation}\boxed{V_B \left(\dfrac{1}{R_1}+\dfrac{1}{R_2}+\dfrac{1}{R_3}\right) = \dfrac{V_A}{R_1} + \dfrac{V_C}{R_2} + \dfrac{V_D}{R_3}}\end{equation}
Les générateurs
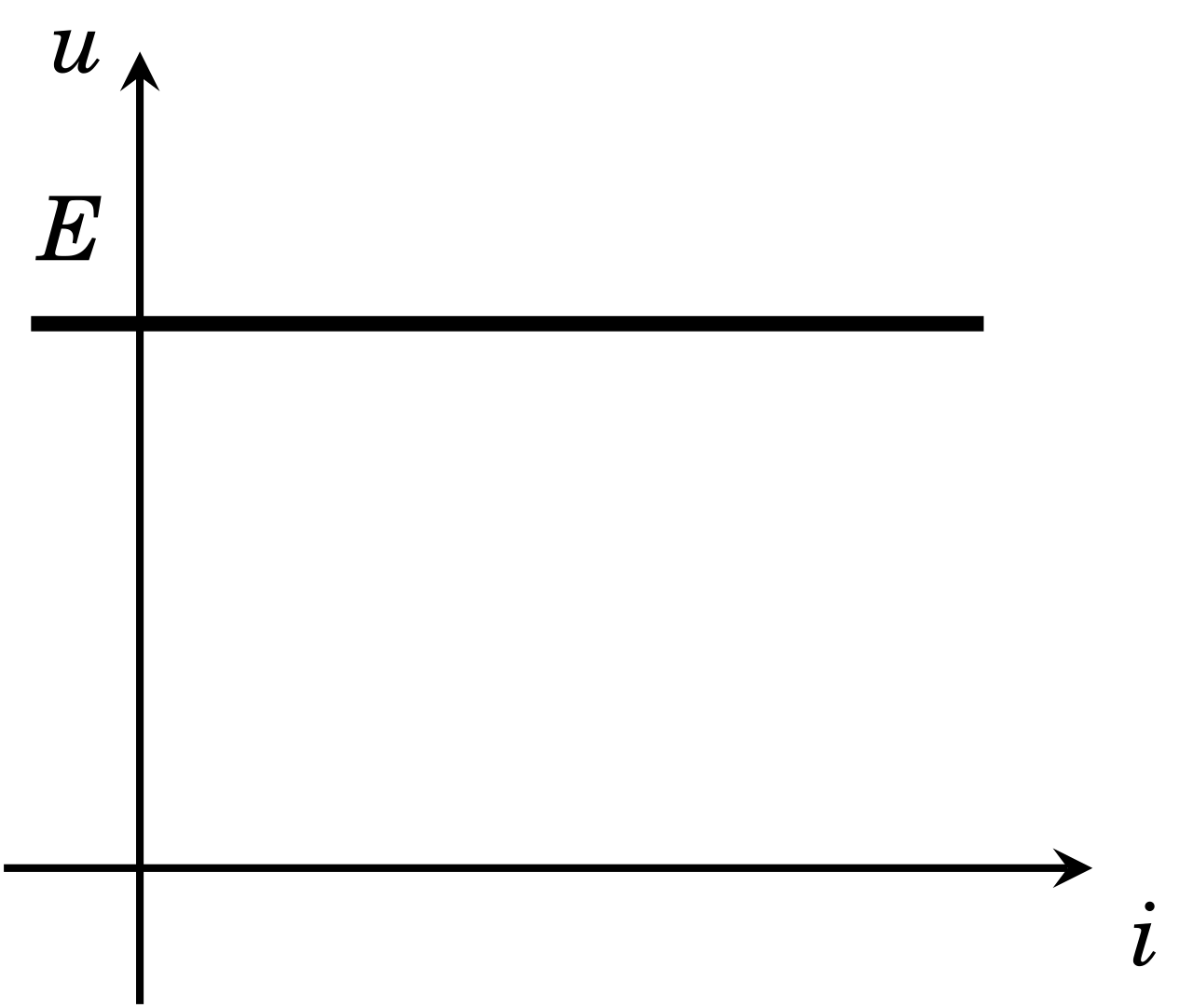
Générateur de tension idéal
Un générateur de tension idéal est un générateur qui délivre une tension constante quel que soit l’intensité débitée.
La tension délivrée est appelée force électromotrice, elle est notée \(E\) et s’exprime en Volt (V).
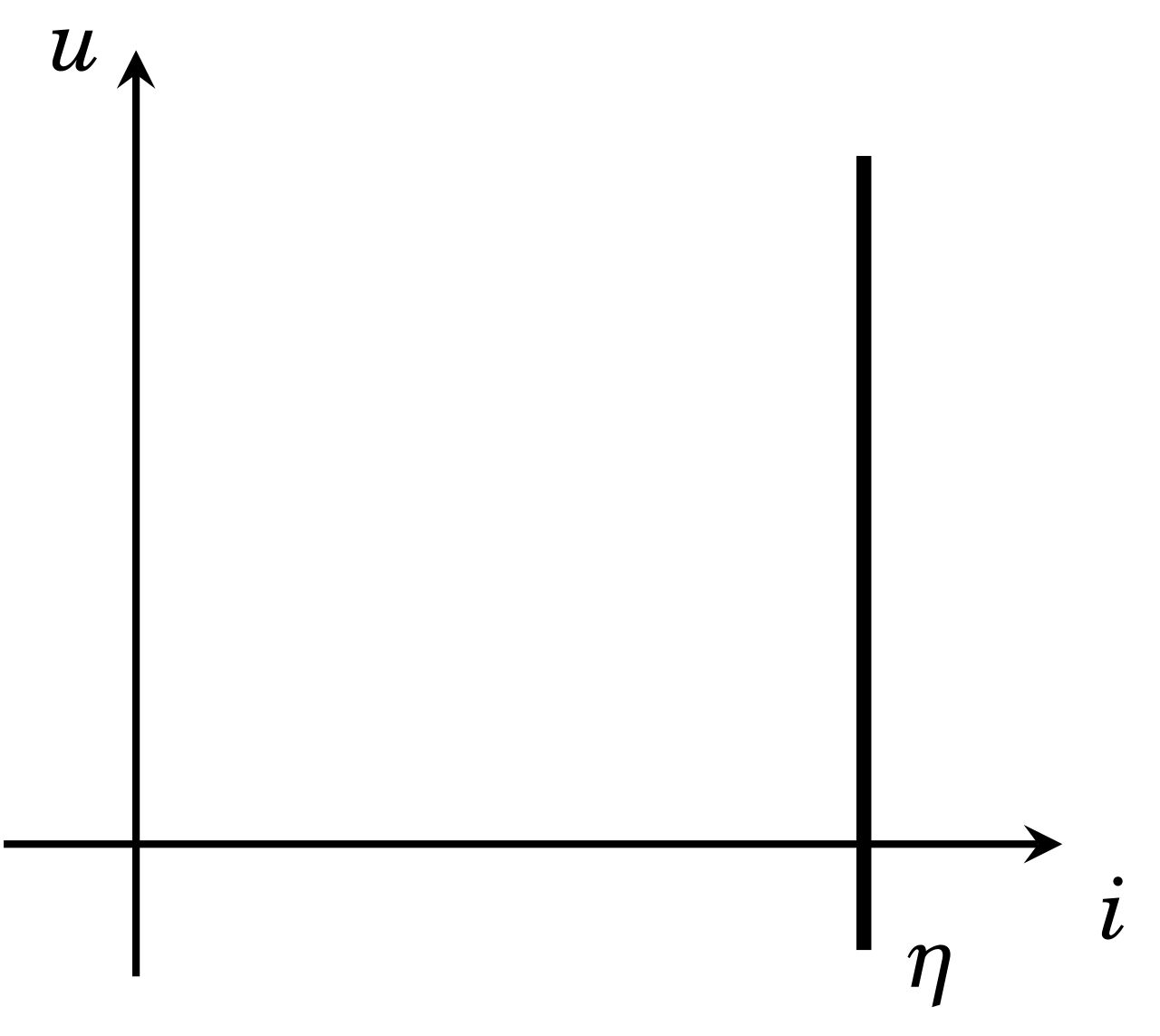
Générateur de courant idéal
Un générateur de courant idéal est un générateur qui délivre une intensité constante quel que soit la tension à ses bornes.
Le courant délivré est appelé courant électromoteur, il est notée \(\eta\) et s’exprime en Ampère (A).
Association de générateurs
L’association en série de deux générateurs de tension idéaux de f.e.m $E_1$ et $E_2$ est équivalente à un générateur de tension idéal qui délivre la force électromotrice \(E_1+E_2\).
L’association en parallèle de deux générateurs de courant idéaux de c.e.m \(\eta_1\) et \(\eta_2\) est équivalente à un générateur de courant idéal qui délivre le courant électromoteur \(\eta_1+\eta_2\).
Modélisation linéaire des générateurs réels
Même si la caractéristique générale d’un générateur n’est pas une droite, les conditions d’utilisation des générateurs montrent que l’on peut localement considérer leur caractéristique comme étant linéaire.
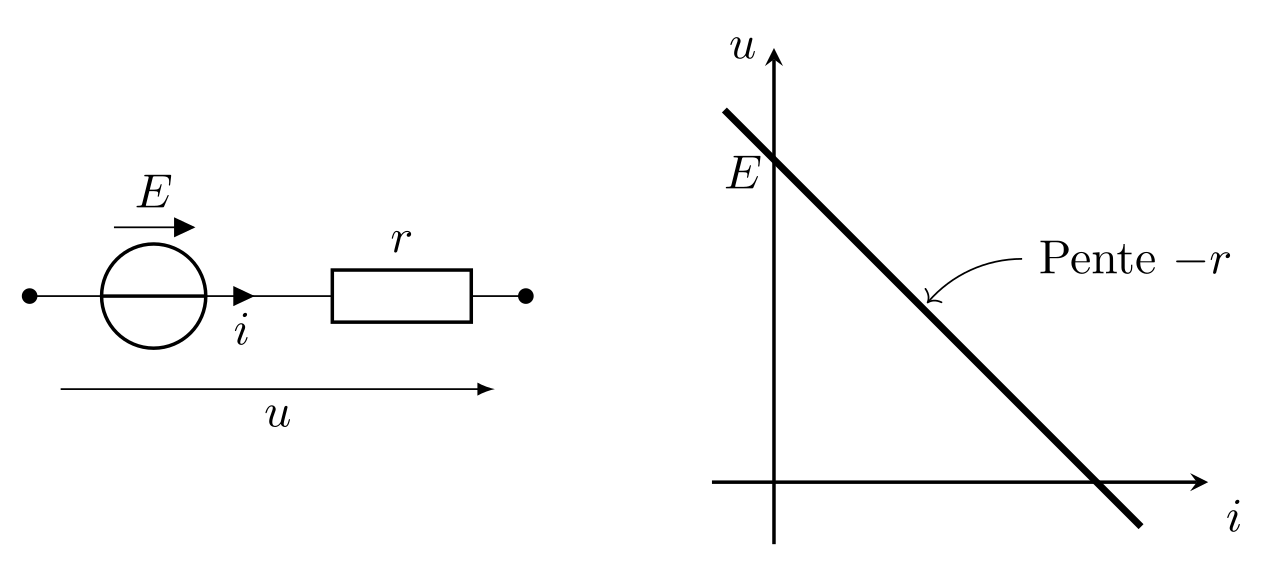
Modèle de Thévenin
Définition
Tout générateur réel peut être modélisé par un générateur idéal de tension de f.e.m \(E\) en série avec une résistance \(r\) appelée résistance interne du générateur et exprimée en Ohm (\(\Omega\)).
Sa caractéristique a pour équation :
\begin{equation}\boxed{u=E-r\times i}\end{equation}
Association
Si deux générateurs de Thévenin (\(E_1\),\(r_1\)) et (\(E_2\),\(r_2\)) sont associés en série, l’ensemble est équivalent à un générateur de Thévenin de f.e.m \(E_1+E_2\) et de résistance interne \(r_1+r_2\).
Modèle de Norton
Définition
Tout générateur réel peut être modélisé par un générateur idéal de courant de c.e.m \(\eta\) en parallèle avec une résistance \(r\) appelée résistance interne du générateur et exprimée en Ohm (\(\Omega\)).
On peut aussi introduire \(g\), conductance interne du générateur exprimée en Siemens (S).
Sa caractéristique a pour équation :
\begin{equation}\boxed{i=\eta - g\times u = \eta-\dfrac{u}{r}}\end{equation}
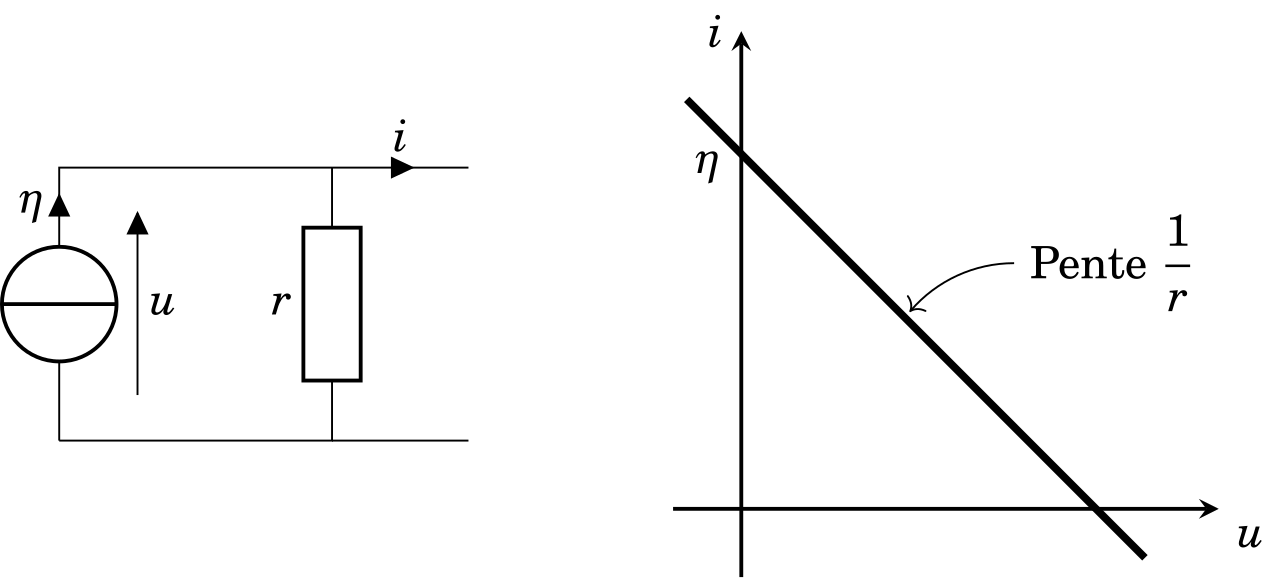
Attention ici, c’est une caractéristique intensité-tension qui est représentée.
Association
Si deux générateurs de Norton identiques (\(\eta_1\),\(g_1\)) et (\(\eta_2\),\(g_2\)) sont associés en parallèle, l’ensemble est équivalent à un générateur de Norton de c.e.m \(\eta_1+\eta_2\) et de conductance interne \(g_1+g_2\).
Passage d’un modèle à l’autre
Les modèles de Thévenin et de Norton sont équivalents, on peut passer de l’un à l’autre à l’aide de la relation :
\begin{equation}\boxed{E=r\,\eta}\end{equation}
Intérêt des modèles de Thévenin et Norton
La transformation Thévenin-Norton permet de mettre en œuvre la méthode des nœuds et la méthode des mailles qui permettent de calculer toutes les tensions entre les nœuds du circuit ou toutes les intensités dans les branches de celui-ci.
Méthode des mailles
On cherche à calculer les intensités dans les branches. Dans cette méthode, on transforme tous les générateurs en modèle de Thévenin, puis on mène les calculs en appliquant à bon escient la loi des mailles et la loi des nœuds vues précédemment.
Méthode des nœuds
Celle-ci permet de calculer les tensions entre les nœuds du circuit. Il faudra pour l’appliquer transformer tous les générateurs en modèle de Norton, puis appliquer la loi des nœuds et la loi des mailles à bon escient.
Bien souvent c’est un mélange de la méthode des nœuds et de la méthode des mailles qui permet de résoudre le problème posé.


