Licence 1 > Electrocinétique > Fourier - Filtres électriques

Fonction de transfert - filtrages

Ce cours est disponible intégralement en vidéos dans une playlist dédiée. La première vidéo est disponible ci-dessous :

Il a été découpé en 8 séquences:

1. Sommaire
2. Système linéaire et séries de Fourier
3. Transformée de Fourier et applications
4. Notion de fonction de transfert, exemples
5. Généralités sur les filtres électriques
6. Etude complète d'un filtre passe-bas
7. Filtre passe-haut, application des filtres passes-bas et passe-haut : le filtre ADSL
8. Filtre passe-bande et application

Introduction

Dans ce cours nous allons définir la fonction de transfert d'un système physique linéaire et l'appliquer à la notion de filtrage électronique. Mais avant d'atteindre l'objectif, nous passerons en revue quelques notions théoriques fondamentales en physique telles que :

• Importance du régime sinusoïdal : décomposition en série de Fourier, spectre en fréquences, notion de fondamental et d'harmoniques ;
• Transformée de Fourier ;
• Passage d'une équation différentielle à une équation linéaire en utilisant le passage en complexe.

C'est alors que nous verrons la notion de fonction de transfert, qui en caractérisant un système donné, nous permet de calculer le signal de sortie si l'on connaît le signal d'entrée.

Nous utiliserons alors la fonction de transfert en l'appliquant aux filtres électriques.

Définition d'un système linéaire - exemples

Système linéaire

On considère un système physique quelconque, que l'on représente de la façon suivante :

Ce système fournit un signal de sortie $s(t)$ dépendant du signal d'entrée $e(t)$.

Généralement, celui-ci est décrit mathématiquement par une équation différentielle temporelle qui relie l'entrée et la sortie :

\begin{equation} a_0\,e(t) + a_1\,\dfrac{\mathrm{d}e(t)}{\mathrm{d}t} + \ldots + a_n\,\dfrac{\mathrm{d}^ne(t)}{\mathrm{d}t^n} = b_0\,s(t) + b_1\,\dfrac{\mathrm{d}s(t)}{\mathrm{d}t} + \ldots + b_n\,\dfrac{\mathrm{d}^ns(t)}{\mathrm{d}t^n} \end{equation}

Cette équation étant linéaire, les systèmes étudiés sont qualifiés de linéaires: un tel système implique la vérification du principe de superposition :

si on connaît les signaux de sortie $s_1(t)$ et $s_2(t)$ correspondant aux entrées $e_1(t)$ et $e_2(t)$, alors la sortie correspondant au signal d'entrée $\lambda_1\,e_1(t) + \lambda_2\,e_2(t)$ est $\lambda_1\,s_1(t) + \lambda_2\,s_2(t)$.

Résoudre cette équation différentielle \eqref{equadiff} revient à connaître la sortie en fonction de l'entrée connue. Malheureusement, cette équation peut être difficile à résoudre.

Exemples

De nombreux systèmes physiques classiques sont linéaires:

• Les circuits électriques composés de conducteur ohmique, de condensateur et de bobine ;
• Un système masse-ressort, que l'on peut exciter sinusoïdalement ;
• Une pièce chauffée par un radiateur, on étudie l'évolution de la température de la pièce avec "comme excitateur" la puissance d'alimentation fournie.

Importance du régime sinusoïdal

Généralités

En physique, on a souvent à faire à des signaux périodiques, voir sinusoïdaux: variation de la température dans une journée, ondes (acoustiques, électromagnétiques, électriques, mécaniques).

D'après la théorie des séries de Fourier, tout signal périodique peut se décomposer en une somme de fonctions sinusoïdales (sinus et cosinus): c'est la décomposition en série de Fourier.

On peut même aller plus loin, en généralisant la décomposition de Fourier à un signal non périodique : en effet, on peut considérer celui-ci comme un signal de période infinie. Dans ce cas on utilise un outil, la transformée de Fourier.

Le but de ce travail mathématique, série de Fourier ou transformée de Fourier, est de pouvoir étudier la sortie du système linéaire $s(t)$ en fonction de n'importe quelle entrée $e(t)$ : on décomposera l'entrée en somme de signaux simples $e_i(t)$, on étudie les sorties $s_i(t)$ pour chaque entrée $e_i(t)$, on recompose la sortie $s(t) = \sum_i s_i(t)$. C'est l'application du principe de superposition qui nous permet cela.

Décomposition en série de Fourier

Pourquoi une somme de sinus et cosinus?

Soit une fonction $f(t)$ périodique de période $T_0 = \dfrac{2\,\pi}{\omega_0}$ que l'on cherche à approcher à l'aide d'une somme de fonctions sinusoïdales, par exemple du type $K\,\sin\,(n\,\omega_0\,t + \varphi)$ avec $n$ un entier positif ou nul.

On cherche donc la décomposition en fonctions de même période ou de période égale à une fraction (un multiple si l'on parle en pulsation) de la période de la fonction que l'on veut approximer.

Imaginons alors la fonction $f(t)$ suivante :

Superposons lui la première fonction sinusoïdale de la décomposition, soit $K\,\sin\,(\omega_0\,t + \varphi)$ (le cas $n=0$ est particulier, cela représenterait la composante continue s'il y en avait une) :

Pour que cette fonction sinus colle au mieux à la fonction $f(t)$, on peut jouer sur son amplitude :

Ou sur sa phase :

Mais il n'est pas très intéressant de faire jouer deux paramètres sur une même fonction. Il est donc plus facile de décomposer chaque fonction $K\,\sin\,(n\,\omega_0\,t + \varphi)$ :

\begin{align} \sin\,(a+b) &= \sin\,a\,\cos\,b + \cos\,a\,\sin\,b \\ \Longrightarrow K\,\sin\,(\omega_0\,t + \varphi) &= K\,\cos\,\varphi\,\sin\,(n\,\omega_0\,t) + K\,\sin\,\varphi\,\cos\,(n\,\omega_0\,t) \\ &= K_1\,\sin\,(n\,\omega_0\,t) + K_2\,\cos\,(n\,\omega_0\,t) \end{align}

Ainsi, au lieu de jouer sur deux paramètres dépendants car propriétés d'une même fonction, on va plutôt décomposer la fonction $f(t)$ en une somme de sinus et de cosinus et ajuster les deux paramètres indépendants qui sont les amplitudes $K_1$ et $K_2$.

Calcul de l'erreur faite entre $f(t)$ et une des fonctions sinusoïdales

Comparons à présent la fonction $f(t)$ et la première fonction sinus :

L'erreur que l'on fait en approximant $f(t)$ par $K_1\,\sin\,\omega_0\,t$ est représentée par l'aire entre les deux courbes :

Mathématiquement, une aire est une intégrale, l'aire entre les deux courbes s'écrit donc :

\begin{equation} \mathcal{A} = \displaystyle\int_0^T (f(t) - K_1\,\sin\,\omega_0\,t)\,\mathrm{d}t \end{equation}

Nous avons un petit problème, car la courbe rouge est tantôt au dessus de la bleue tantôt en dessous, ainsi l'aire \eqref{mcalA} est parfois positive (partie hachurées) parfois négative (parties pointés).

Nous pourrions travailler en valeur absolue, mais il faudrait alors distinguer les cas ce qui n'est pas pratique.

Sachant que nous cherchons à minimiser cette aire, et que mathématiquement, le minimum de la fonction $\mathcal{A} = \displaystyle\int_0^T (f(t) - K_1\,\sin\,\omega_0\,t)\,\mathrm{d}t$ et celui de la fonction $\mathcal{A^*} = \displaystyle\int_0^T (f(t) - K_1\,\sin\,\omega_0\,t)^2\,\mathrm{d}t$ sont identiques, nous utiliserons cette dernière intégrale qui évite le problème des intégrales signées.

Il nous faut à présent déterminer le minimum de la fonction en question, ceci se fait grâce à la dérivée, et rappelons nous que l'on cherche à ajuster le paramètre $K_1$ pour que l'aire entre les deux courbes soient minimales.

Ainsi on veut :

\begin{align} &\dfrac{\mathrm{d}\mathcal{A^*}}{\mathrm{d}K_1} = 0 \\ \Longleftrightarrow \; &\dfrac{\mathrm{d}}{\mathrm{d}K_1}\displaystyle\int_0^T (f(t) - K_1\,\sin\,\omega_0\,t)^2\,\mathrm{d}t = 0 \\ \Longleftrightarrow \; &\dfrac{\mathrm{d}}{\mathrm{d}K_1}\left(\displaystyle\int_0^T f(t)^2\,\mathrm{d}t + \displaystyle\int_0^T K_1^2\,\sin^2\,(\omega_0\,t)\,\mathrm{d}t - \displaystyle\int_0^T 2\,K_1\,f(t)\,\sin\,(\omega_0\,t)\,\mathrm{d}t\right) = 0 \\ \Longleftrightarrow \; & 0 + 2\,K_1\,\displaystyle\int_0^T \sin^2\,(\omega_0\,t)\,\mathrm{d}t - 2\,\displaystyle\int_0^T f(t)\,\sin\,(\omega_0\,t)\,\mathrm{d}t = 0 \\ \Longleftrightarrow \; & 2\,K_1\,\dfrac{T}{2} - 2\,\displaystyle\int_0^T f(t)\,\sin\,(\omega_0\,t)\,\mathrm{d}t = 0 \\ \Longleftrightarrow \; & K_1 = \dfrac{2}{T}\displaystyle\int_0^T f(t)\,\sin\,(\omega_0\,t)\,\mathrm{d}t \end{align}

On a donc trouver l'expression du paramètre $K_1$ permettant de minimiser l'erreur fait quand on approxime $f(t)$ à l'aide de $K_1\,\sin\,\omega_0\,t$. On peut généraliser avec toutes les fonctions sinus et les fonctions cosinus. On note généralement les paramètres $a_n$ pour les $\cos\,$ et $b_n$ pour les $\sin$.

Valeur moyenne, fondamental et harmoniques

Le terme $\dfrac{a_0}{2} = \dfrac{1}{T}\displaystyle\int _0^T f(t)\,\mathrm{d}t$ qui est distingué dans ces décompositions représente la valeur moyenne du signal (la composante continue).

Lorsque $n=1$, on parle de la composante fondamentale du signal caractérisée par $a_1$ et $b_1$.

Pour tout autre valeur de $n$, on parle d'harmonique de rang $n$ caractérisée par les valeurs de $a_n$ et $b_n$.

Remarques

• Nous avons expliqué l'obtention des coefficients de Fourier en partant d'une fonction en $K_n\,\sin\,(n\,\omega_0\,t + \varphi)$ alors qu'on a une fonction en $c_n\,\cos\,(n\,\omega_0\,t + \varphi)$ dans les formules précédentes : cela n'a pas d'importance, $\sin\,\theta = \cos\,\left(\dfrac{\pi}{2}-\theta\right)$.
• En cas de fonction $f(t)$ paire ou impaire, les coefficients de la décomposition de Fourier sont simplifiés, notamment :
• si $f(t)$ est paire, $b_n = 0$ ;
• si $f(t)$ est impaire, $a_n = 0$.

Cas des fonctions paires et impaires

Fonction paire
Si $s(t)$ est une fonction paire alors $s(t)\cos(n\omega t)$ est paire. On a : $\displaystyle a_n = \dfrac{4}{T}\,\int_{0}^{\frac{T}{2}}\,s(t)\,\cos (n\omega t)\,\mathrm{d}t$ pour $n\neq 0$ et $\displaystyle a_0 = \dfrac{2}{T}\int_0^{\frac{T}{2}}s(t) \mathrm{d}t$.

La fonction $s(t)\,\sin\,(n\omega t)$ est impaire et $b_n = 0$.

Fonction impaire

Si $s(t)$ est une fonction impaire alors $s(t)\,\cos(n\omega t)$ est impaire et $a_n=0,\;\forall n$.

La fonction $s(t)\sin(n\omega t)$ est paire.
On a donc : $\displaystyle b_n = \dfrac{4}{T}\int_0^{\frac{T}{2}}s(t) \sin\,(n\omega t) \,\mathrm{d}t$.

Spectres

A l'issue de la décomposition d'un signal "complexe" périodique en série de Fourier, on peut tracer deux spectres :

• Le spectre d'amplitude : on représente sur un graphique l'amplitude de chacun des termes de la décomposition en série de Fourier en fonction de la fréquence (ou pulsation) soit $c_n = f(\omega_n)$ ;
• Le spectre de phase : on peut représenter la phase de chaque terme en fonction de la fréquence soit $\varphi_n=f(\omega_n)$.

Illustrons cela en comparant la représentation temporelle et spectrale de notre signal de départ :

Signal "complexe" initial

Signal après décomposition en série de Fourier

Application à l'acoustique musicale

Le son des instruments est un signal souvent "complexe" mais périodique, une décomposition en série de Fourier permet de connaître les composantes fréquentielles principales qui interviennent dans un son.

Prenons un La 440, qui sert souvent de référence aux musiciens pour accorder leur instrument. Comparons les signaux et spectres pour différents instruments simulés par un synthétiseur :

Pour un piano

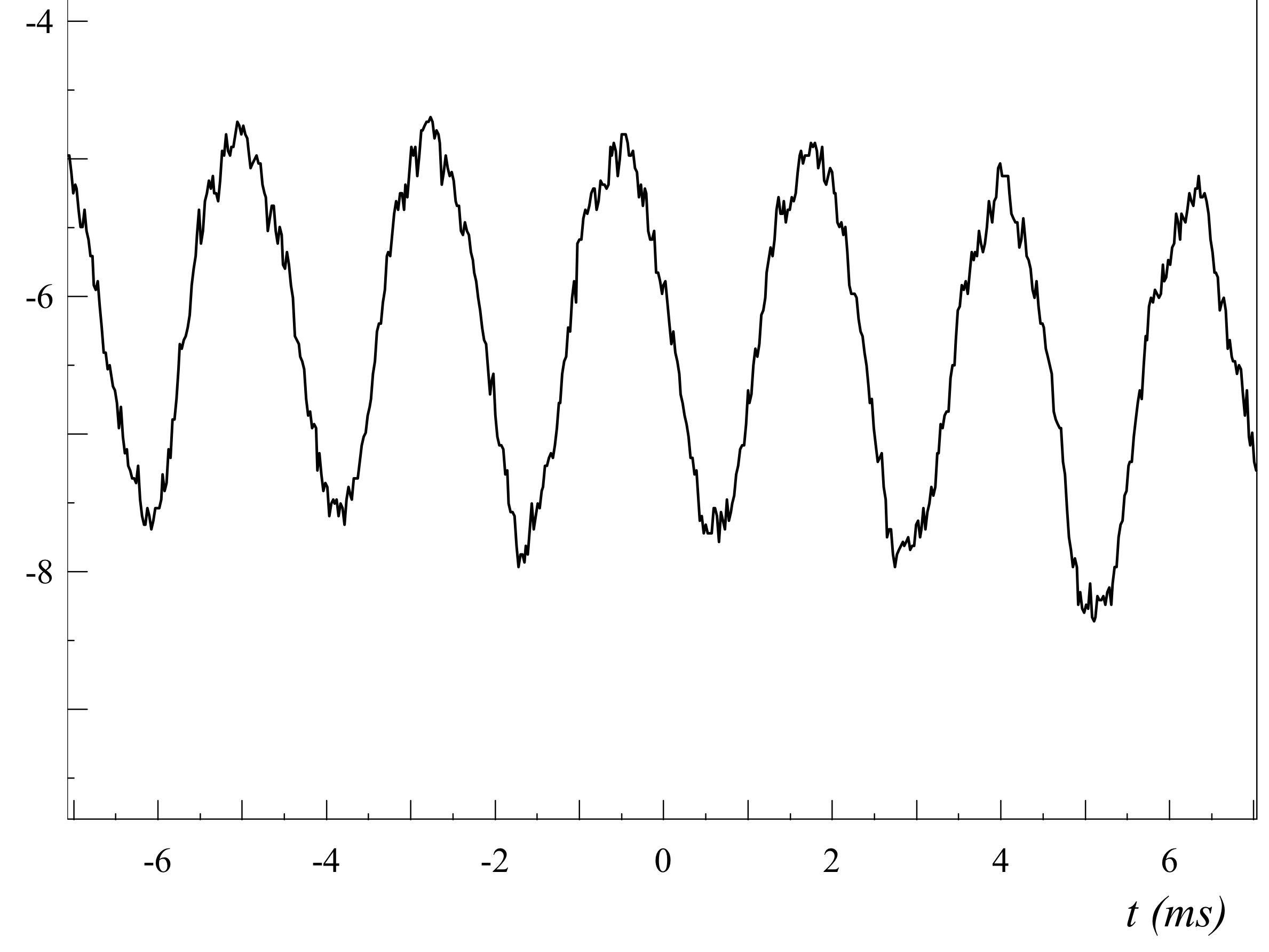
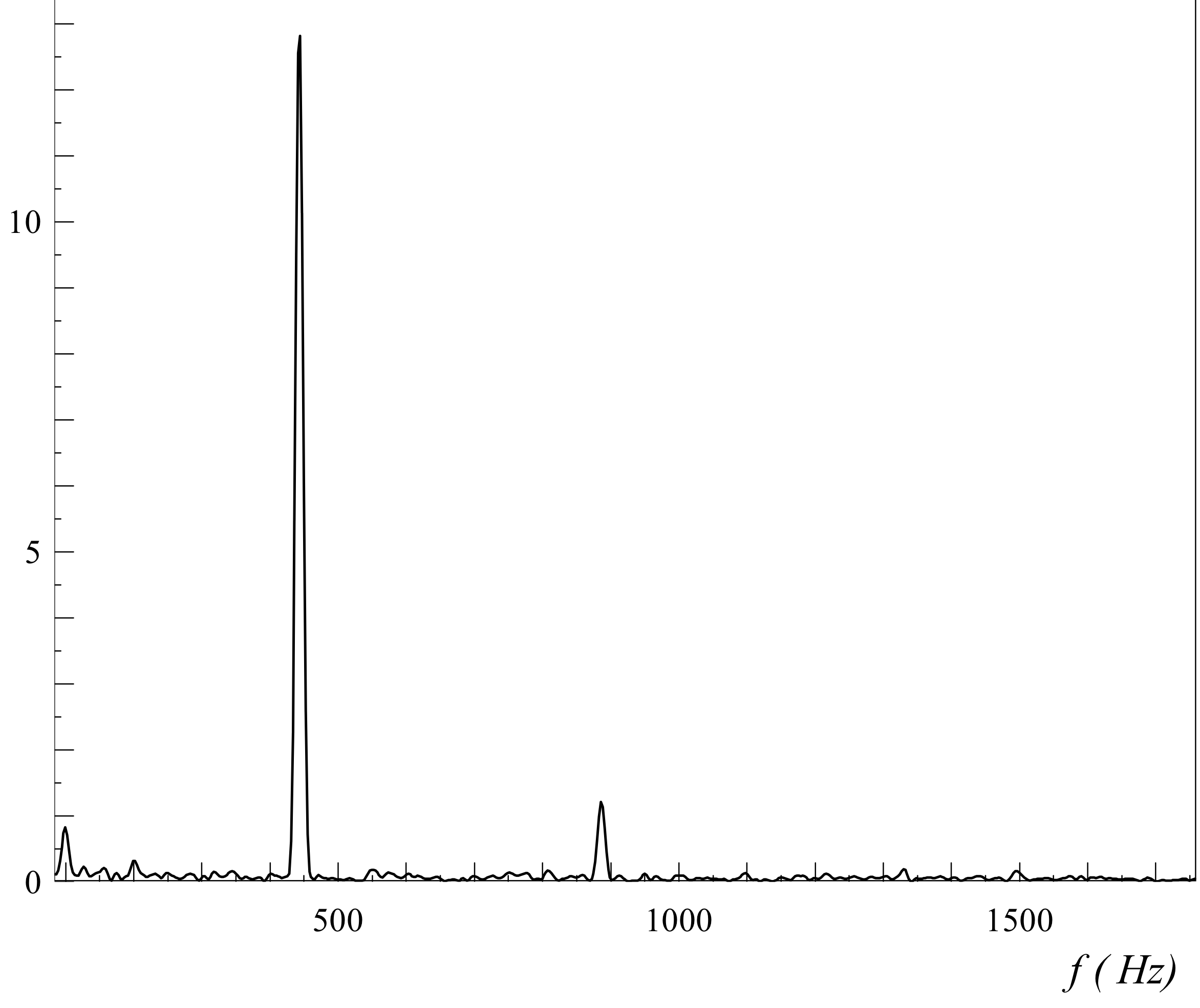
Le signal est quasiment sinusoïdal, nous ne sommes pas surpris d'obtenir un spectre avec quasiment que le fondamental qui apparaît, à 440 Hz.

Pour une trompette

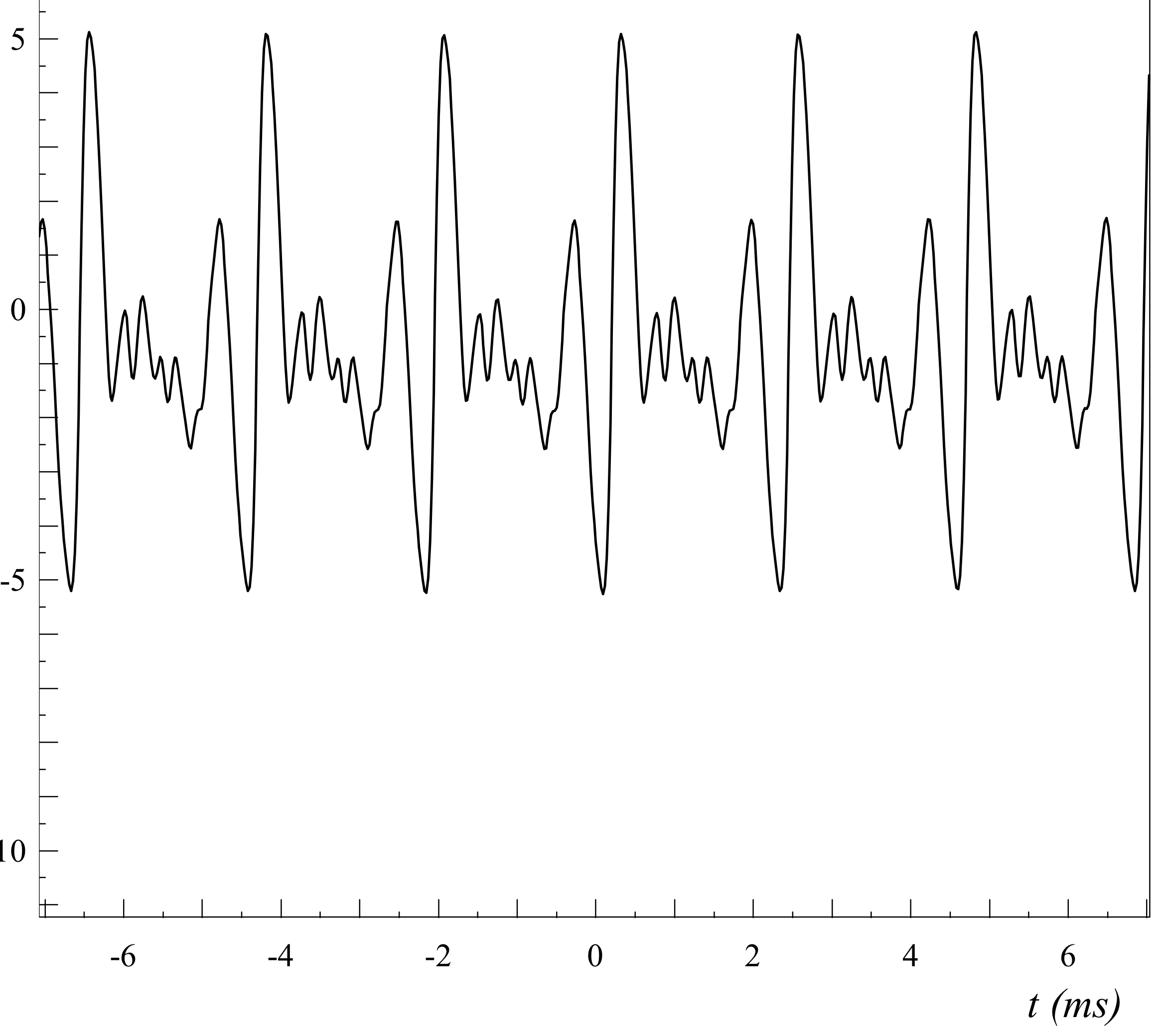
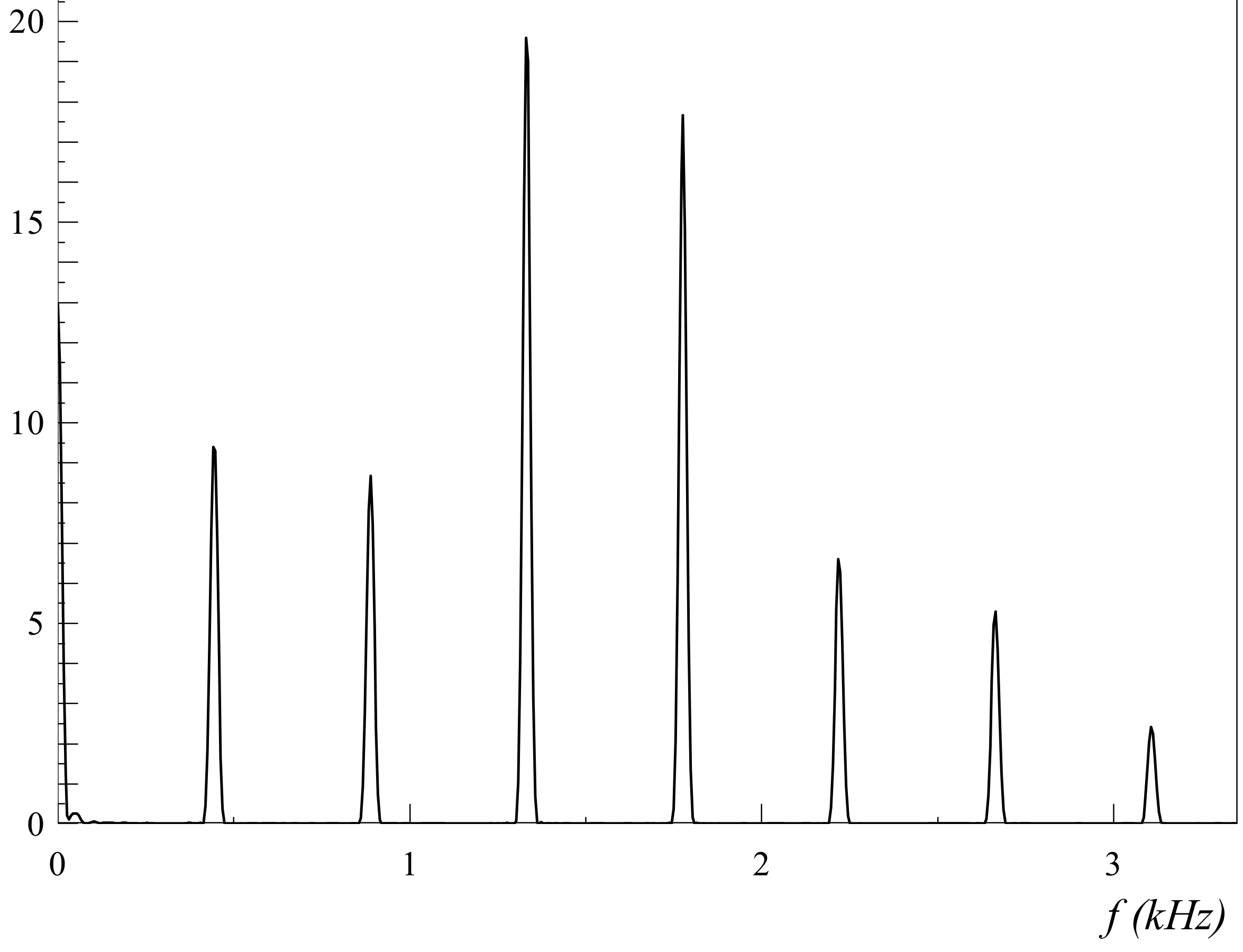
On a un signal temporelle bien plus complexe, et donc un spectre en fréquence riche en harmoniques. On voit même que l’intensité des harmoniques compris entre 1 et 2 kHz est importante.
C’est cette signature fréquentielle qui donne le timbre de l’instrument.

Pour une violon

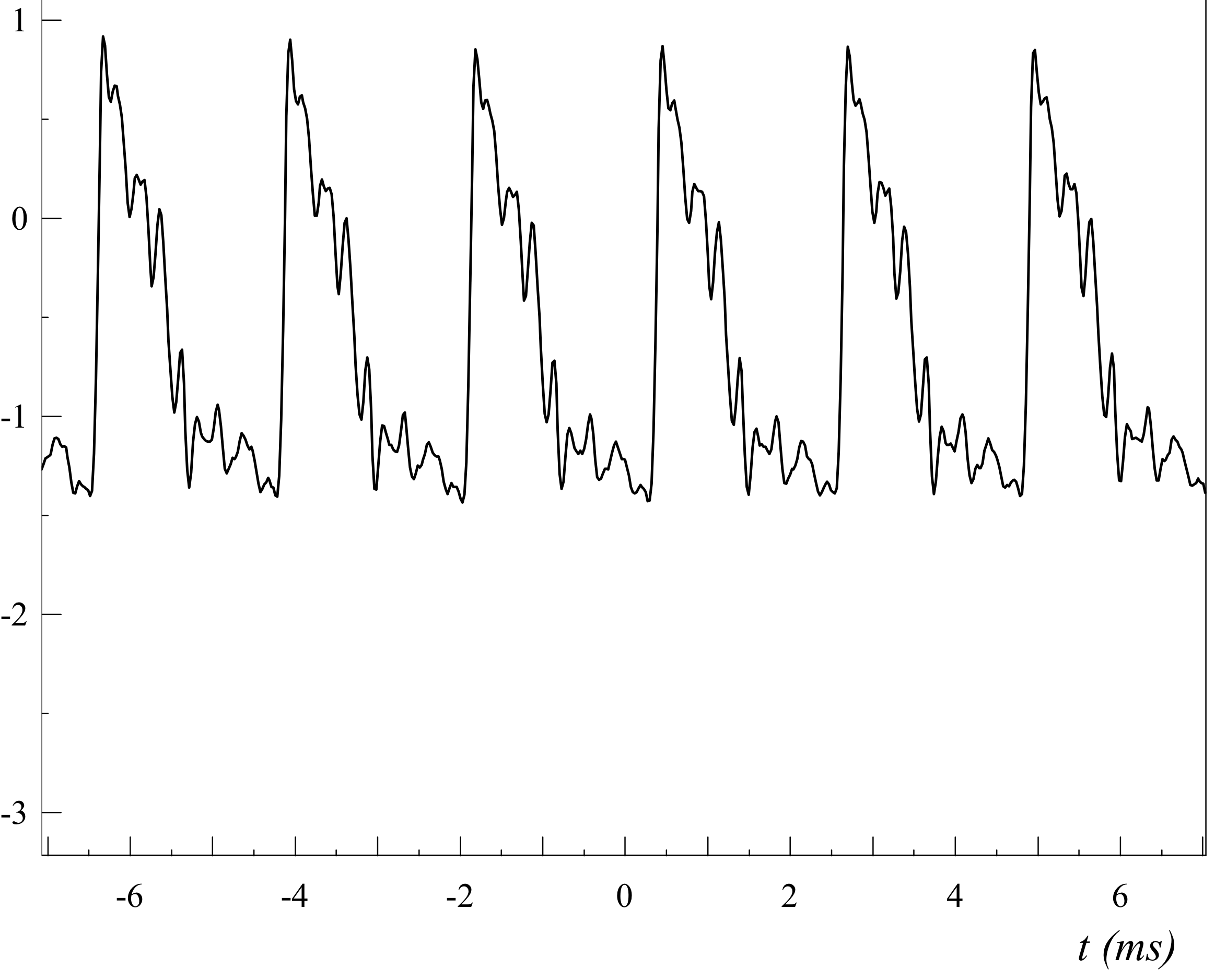
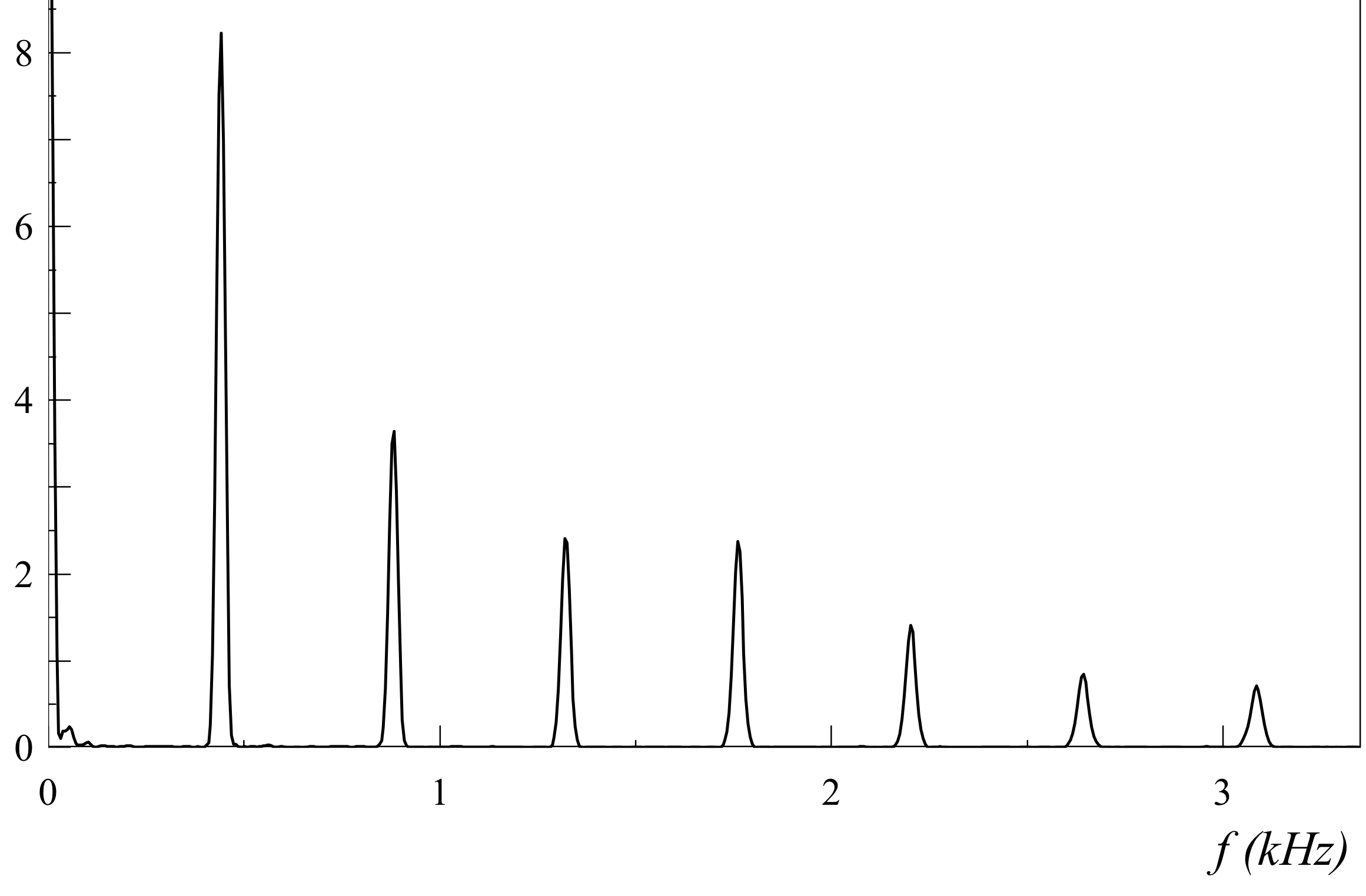
Le signal est différent de celui de la trompette, pourtant il est composé des mêmes harmoniques. Le timbre du violon est différent de celui de la trompette car l'intensité de chaque harmonique est différente.

Notion de transformée de Fourier

Théorie

Comme nous l'avons évoqué précédemment, la théorie de la décomposition en série de Fourier, qui ne fonctionne que pour des signaux périodiques, peut-être généralisée avec des fonctions non périodiques. On passe de l'un à l'autre en considérant qu'un signal non périodique est un signal périodique de période qui tend vers l'infini.

Nous n'allons pas démontrer mathématiquement le passage de série de Fourier à transformée de Fourier car cela s'avère complexe, nous retiendrons juste le résultat :

\begin{equation} F(\omega) = \dfrac{1}{\sqrt{2\,\pi}}\displaystyle\int_{-\infty}^{\infty}\,f(t)\,e^{-i\,\omega\,t}\,\mathrm{d}t \end{equation}

est la transformée de Fourier de la fonction $f(t)$. Cela permet de passer du domaine temporel au domaine spectral (fréquence ou pulsation). A noter que comme on considère la période du signal infinie, la pulsation $\omega$ tend vers 0 $\displaystyle\left( \text{ on rappelle que } \omega = \dfrac{2\pi}{T}\right)$ : autrement dit, le spectre n'est pas discret (pas de fondamental $f$ et d'harmoniques $f_n = n\,f$), mais un spectre continu.

\begin{equation} f(t) = \dfrac{1}{\sqrt{2\,\pi}}\displaystyle\int_{-\infty}^{\infty}\,F(\omega)\,e^{i\,\omega\,t}\,\mathrm{d}\omega \end{equation}

est la transformée de Fourier inverse de la fonction $F(\omega)$. Elle permet de passer du domaine spectral au domaine temporel.

Applications

Train d'onde et largeur de raie spectrale

En optique, le spectre d'une source lumineuse dépend de la longueur des trains d'ondes émis par ses atomes. On peut comparer les spectres de deux sources plus ou moins monochromatiques. Le spectre $F(\nu)$ est obtenu par le calcul de la transformée de Fourier de la fonction $f(t)$ qui représente le train d'onde.

Le spectre d'un laser He-Ne est quasiment monochromatique, il présente une unique raie à la fréquence $\nu_0$ correspondant à la longueur d'onde du laser. Ainsi, on peut considérer que les trains d'onde émis par cette source sont des sinusoïdes infinies :

Si on considère une lampe à vapeur de mercure, on peut observer une raie verte qui n'est pas monochromatique, le spectre associé montre une certaine largeur de raie qui signifie que les trains d'onde émis pour former cette raie verte sont beaucoup plus court que dans le cas du laser:

Diffraction des rayons X par un cristal

L'étude de cristaux se fait également grâce à la transformée de Fourier : les atomes d'un cristal sont disposés régulièrement dans l'espace de façon triplement périodique (réseau).

On envoie un pinceau de rayon X monochromatique sur un cristal que l'on met en rotation. Les électrons des atomes diffractent les rayons, on récupère alors le résultat de cette diffraction sur un capteur CCD: on obtient une répartition de taches de diffraction (réseau réciproque) qui est la transformée de Fourier du cristal.

Si l'amplitude diffractée est définie par une fonction $F(X,Y,Z)$ on remonte à la densité électronique du cristal définie par une fonction $f(x,y,z)$. On peut alors en déduire la répartition tridimensionnelle des atomes du cristal et les liaisons entre ces atomes.

Notion de fonction de transfert

Revenons à présent au cœur de notre chapitre. Rappelons qu'une fois la fonction de transfert d'un système est établie, on peut connaître le signal de sortie pour n'importe quel signal d'entrée.

Rappels sur le régime sinusoïdal

Lorsque l'on passe en régime sinusoïdal, on considère que l'entrée est une fonction complexe $\underline{e}(t) = E\,e^{j(\omega\,t+\varphi_e)} =\underline{E}\,e^{j\,\omega\,t}$ et la sortie une fonction complexe $\underline{s}(t) = S\,e^{j(\omega\,t+ \varphi_s)} = \underline{S}\,e^{j\,\omega\,t}$.

Les nombres complexes $\underline{E} = E\,e^{j\,\varphi_e}$ et $\underline{S}= S\,e^{j\,\varphi_s}$ sont appelés amplitudes complexes, ils contiennent les informations d'amplitude et de phase.

Le grand intérêt du passage en complexe est de transformer une équation différentielle en équation linéaire car, en régime sinusoïdal:

\begin{equation} \dfrac{\mathrm{d}}{\mathrm{d}t} \equiv \times j\,\omega \qquad \qquad \int \mathrm{d}t \equiv \times \dfrac{1}{j\,\omega} \end{equation}

Définition de la fonction de transfert

La fonction de transfert complexe d'un système traité en régime sinusoïdal s'écrit :

\begin{equation} \underline{H}(j\,\omega) = \dfrac{\underline{S}}{\underline{E}} \end{equation}

L'intérêt de cette fonction est qu'une fois déterminée, il suffit de multiplier l'entrée par la fonction de transfert pour connaître la sortie.

Cette fonction donne accès :

• Au rapport des amplitudes, en prenant le module de la fonction de transfert complexe: \begin{equation} |\underline{H}(j\,\omega)| = H(j\,\omega) = \dfrac{S}{E} \end{equation}
\item Au déphasage, en prenant son argument : \begin{equation} \varphi_s - \varphi_e = \mathrm{Arg}(\underline{H}(j\,\omega)) \end{equation}

Exemple de fonction de transfert en mécanique

On étudie le comportement d'un chariot qui se déplace sans frottement le long d'un axe O$x$, celui-ci est soumis à deux forces, la force de rappel d'un ressort et une force de frottement fluide exercé par un amortisseur:

On prend la position d'origine de l'axe coïncidant à la longueur à vide du ressort.
Appliquons le principe fondamental de la dynamique au chariot dans le référentiel terrestre galiléen.

\begin{align} m\,\overrightarrow{a} = \sum \overrightarrow{F}_\mathrm{ext} \\ m\,\ddot x = -k\,x - \lambda\,\dot x + f(t) \\ \ddot x + \dfrac{\alpha}{m}\,\dot x + \frac{k}{m}\,x = f(t) \end{align}

Considérons à présent le régime sinusoïdal : si l'entrée $f(t)$ est sinusoïdal, alors la sortie $x(t)$ l'est également.

On pose donc $\underline{f}(t) = E\,e^{j\,\omega\,t+\varphi_e}$ pour l'entrée et $\underline{x}(t) = S\,e^{j\,\omega\,t + \varphi_s}$. L'équation différentielle devient:

\begin{equation} \left(-\omega^2 + j\,\omega\,\dfrac{\alpha}{m} + \dfrac{k}{m} \right)\,S\,e^{j\,\varphi_s} = E\,e^{j\,\varphi_e} \end{equation}

La fonction de transfert vaut donc : \begin{equation} \underline{H}(j\,\omega) = \dfrac{\underline{S}}{\underline{E}} = \dfrac{1}{\left(\dfrac{k}{m}-\omega^2\right)+j\,\dfrac{\alpha}{m}\,\omega} \end{equation}

Si on pose, comme classiquement, $\omega_0^2 = \dfrac{k}{m}$ la pulsation propre d'oscillation du système et $\lambda = \dfrac{\alpha}{2\,m}$ le coefficient d'amortissement, la fonction de transfert s'écrit : \begin{equation} \underline{H}(j\,\omega) = \dfrac{1}{\left(\omega_0^2-\omega^2\right)+j\,2\,\lambda\,\omega} \end{equation}

On pose $\omega_0^2 = \dfrac{1}{LC}$ la pulsation propre d'oscillation du système et $\lambda = \dfrac{R}{2\,L}$ le coefficient d'amortissement, la fonction de transfert s'écrit:

\begin{equation} \underline{H}(j\,\omega) = \dfrac{\underline{S}}{\underline{E}} = \dfrac{1}{\left(\omega_0^2-\omega^2\right)+j\,2\,\lambda\,\omega} \end{equation}

On retrouve la même fonction de transfert qu'en mécanique par analogie électromécanique.

Exemple de fonction de transfert en électrocinétique

On étudie le comportement d'un circuit RLC série soumis à une tension sinusoïdale d'entrée $e(t)$, le signal de sortie $s(t)$ est pris aux bornes du condensateur:

Le diviseur de tension (ou la loi des mailles) en régime sinusoïdal permet d'écrire :

\begin{equation} \underline{S} = \dfrac{\dfrac{1}{j\,C\,\omega}}{R+j\,L\,\omega + \dfrac{1}{j\,C\,\omega}}\,\underline{E} = \dfrac{1}{j\,R\,C\,\omega -L\,C\,\omega^2 + 1}\,\underline{E} = \dfrac{1}{\dfrac{1}{LC}-\omega^2 + j\,\dfrac{R}{L}\,\omega}\,\underline{E} \end{equation}

On pose $\omega_0^2 = \dfrac{1}{LC}$ la pulsation propre d'oscillation du système et $\lambda = \dfrac{R}{2\,L}$ le coefficient d'amortissement, la fonction de transfert s'écrit:

\begin{equation} \underline{H}(j\,\omega) = \dfrac{\underline{S}}{\underline{E}} = \dfrac{1}{\left(\omega_0^2-\omega^2\right)+j\,2\,\lambda\,\omega} \end{equation}

On retrouve la même fonction de transfert qu'en mécanique par analogie électromécanique.

Etude approfondie des filtres en électrocinétique

Notion de quadripôle

Les filtres que nous allons étudier pourront être considérer comme des quadripôles linéaires:

\item on leur applique une tension d'entrée, souvent par leur connexion avec un générateur~;
• ils délivrent une tension de sortie entre deux points, qui pourra être reliée à une charge.

On notera que ce quadripôle sera considéré comme linéaire si tous ses composants sont linéaires (leur caractéristique $U=f(I)$ est une droite).

Gain, diagramme de Bode, bande passante

Gain en décibels

Cette nouvelle grandeur va permettre de quantifier l'amplification du montage. Comme celle-ci peut être importante, on préfère utiliser une grandeur logarithmique appelé gain en tension et exprimée en décibels (dB).

Ce gain est défini par:

\begin{equation} \boxed{G_{\mathrm{dB}} = 20 \log \left(|H(j\omega)|\right) = 20 \log \left(\dfrac{S}{E}\right)} \end{equation}

où $|H(j\omega)|$ est l'amplification de tension, $E$ et $S$ sont les amplitudes réelles des signaux $\underline{e}(t)$ et $\underline{s}(t)$.

Diagramme de Bode

Comme nous l'avons dit précédemment, l'intérêt d'un filtre est de pouvoir sélectionner, parmi la multitude de fréquences que comporte un signal d'entrée, une bande de fréquence choisie.

Ainsi, il paraît naturel d'étudier le comportement de ces filtres en fonction de la fréquence, donc de tracer l'allure de leur fonction de transfert en fonction de celle-ci.

Ce travail donne naissance au diagramme de Bode qui est constitué de deux graphiques:

• Un graphique représentant le gain en décibels en fonction de la pulsation avec une échelle logarithmique;
• Un graphique représentant la phase en fonction de la pulsation avec une échelle logarithmique.

Bande passante et fréquences de coupure

Définition

La bande passante est la bande de fréquence qu'un filtre va laisser passer, pour laquelle l'amplification est bonne.

En dehors de celle-ci, les signaux sont très atténués.

Obtention

La bande passante est l'intervalle de fréquence compris entre deux fréquences appelées fréquences de coupure.

Ces fréquences de coupure sont définies par les fréquences qui vérifient :

\begin{equation} G_{\mathrm{dB}} = G_{\mathrm{dB} \mathrm{max}} - 3\mathrm{dB} \qquad \text{ou} \qquad H = \dfrac{H_{\mathrm{max}}}{\sqrt{2}} \end{equation}

Remarques

Dans le cas où il n'y a qu'une fréquence de coupure, deux cas se distinguent :

• Si la seule fréquence de coupure qui existe est basse $f_{c1}$, alors la bande passante n'est pas définie;
• Si la seule fréquence de coupure est haute $f_{c2}$, la bande passante est définie par l'intervalle [0 , $f_{c2}$].

Généralité sur l'étude de différents filtres

Suivant l'allure de du diagramme de Bode en gain, c'est à dire la courbe $G$ en fonction de la fréquence $f$, on donne un nom au quadripôle. On distingue 4 circuits classiques :

Lorsque le signal d'entrée est périodique mais non sinusoïdal, on étudie la façon dont chaque harmonique est atténué et déphasé. On obtient à la sortie, un signal de même fréquence mais de forme différente. L'analyse harmonique des signaux en entrée et en sortie permet d'obtenir une information sur la réponse fréquentielle du filtre. En effet, si la tension d'entrée s'écrit

\begin{equation} e(t)=a_{0}+\sum_{n=1}^{\infty}c_{n\,\mathrm{e}}\cos(2\pi nft+\varphi_{n}) \end{equation}

où les $c_{n\,\mathrm{e}}$ sont les amplitudes des harmonique issus de la décomposition de Fourier du signal d'entrée, on obtient en sortie :

\begin{equation} s(t)=G(0)\times a_{0}\ +\sum_{n=1}^{\infty}G(f_n)\times c_{n\,\mathrm{e}}\cos(2\pi nft+\varphi_{n}+\phi(f_n)) \end{equation}

$G(f_n)$ représente l'atténuation, $\phi(f_n)$ le déphasage.

Il est donc possible de remonter à la réponse fréquentielle du filtre à partir des coefficients de Fourier des signaux en entrée et en sortie puisque

\begin{equation} \displaystyle c_{n\,\mathrm{s}}=G(f_n)\,c_{n\,\mathrm{e}} \end{equation}

Étude d'un filtre passe-bas du premier ordre

Présentation

Le filtre est composé d'un conducteur ohmique et d'un condensateur comme le montre le montage ci-contre.

Ce filtre est appelé filtre du premier ordre car l'équation différentielle qui régit ce système est du premier ordre (voir cours d'électrocinétique de première année).

Aussi, on appellera ce filtre un filtre passif car ses composants n'apportent pas d'énergie au système. A contrario, les filtres basés sur des amplificateurs opérationnels (A.L.I pour amplificateur linéaire intégré), alimentés par une source extérieure, permettent un gain énergétique.

Remarque

On ne va s'intéresser ici qu'aux fonctions de transfert intrinsèque des filtres, c'est à dire que l'on considère que même s'il y a une charge reliée au filtre (branchée en dérivation sur le condensateur), celle-ci est d'impédance infinie si bien que la résistance et le condensateur du filtre peuvent être considérés comme branchés en série.}

Étude rapide

Nous connaissons le comportement en fréquence d'un condensateur. Cela nous permet de faire une étude rapide de ce filtre et de le catégoriser dans les filtres passe-bas. En effet :

• Lorsque la fréquence (ou la pulsation) est basse, l'impédance du condensateur qui a pour expression $\underline{Z}_C=\dfrac{1}{jC\omega}$ tend vers l'infini, le condensateur se comporte alors comme un interrupteur ouvert :
  La tension $\underline{s}(t)$ est égale à la tension $\underline{e}(t)$ : les basses fréquences sont transmises.

• Lorsque la fréquence (ou la pulsation) est haute, l'impédance du condensateur tend vers 0, le condensateur se comporte comme un interrupteur fermé :
  La tension $\underline{s}(t)$ est nulle (tension aux bornes d'un fil) : les hautes fréquences sont atténuées.

Fonction de transfert

En utilisant le diviseur de tension, on établit que :

\begin{equation} \underline{H}(j\omega) = \dfrac{\underline{Z_C}}{\underline{Z_C} + \underline{Z_R}} = \dfrac{1}{1+jRC\omega} \end{equation}

L'ordre du filtre est aussi déterminé par l'ordre en $j\omega$ du polynôme du dénominateur de la fonction de transfert : ici, il s'agit d'un premier ordre.

Forme canonique de la fonction de transfert

Pour pouvoir l'écrire, il faut définir quelques grandeurs :

Amplification en tension

On peut obtenir la fonction amplification de tension en prenant le module de la fonction de transfert :

\begin{equation} \boxed{|H(j\omega)|=\dfrac{1}{\sqrt{1+(RC\omega)^2}}} \end{equation}

Fonction de transfert statique

La fonction de transfert statique, notée $H_0$ et appelée amplification statique, correspond à $\lim_{x\to0} H(j\,\omega)$ :

\begin{equation} H_0 = 1 \end{equation}

Pulsation de coupure et bande passante

La pulsation de coupure correspond à la pulsation pour laquelle $|H(j\omega_C)| = \dfrac{1}{\sqrt{2}}$. On obtient $\omega_C = \dfrac{1}{RC}$. La bande passante est donc [0,$\omega_C$].

Équation canonique de la fonction de transfert

On fait intervenir la fonction statique et la variable réduite $x = \dfrac{\omega}{\omega_C}$ ce qui nous permet d'obtenir :

\begin{equation} \underline{H}(jx) = \dfrac{H_0}{1+jx} \text{ avec } x = \dfrac{\omega}{\omega_C} \end{equation}

Cette expression est générale pour les filtres passe-bas du premier ordre.

Diagramme de Bode

L'expression canonique de la fonction de transfert va nous permettre une étude plus aisée afin d'établir le diagramme de Bode.

Cherchons le comportement asymptotique de la fonction de transfert complexe, pour avoir directement accès à celui de $G_\mathrm{dB}$ et $\phi$ :

On travaille sur la fonction :

\begin{equation*} \underline{H}(j\,x) = \dfrac{H_0}{1+j\,x} \end{equation*}

• Lorsque $x \rightarrow 0$, $\underline{H}(j\,x) \rightarrow H_0 \Longrightarrow \begin{cases} G_{\mathrm{dB}} \rightarrow 20 \log H_0 = G_0 = 0 \\ \phi \rightarrow \mathrm{Arg}(H_0) = 0 \end{cases}$
  
  la première asymptote a pour équation $G_{\mathrm{dB}} = 0$ pour le gain et $0$ pour la phase ;
• Lorsque $x \rightarrow \infty$ ou $x \gg 1$, $\underline{H}(j\,x) \rightarrow -\dfrac{j\,H_0}{x} \Longrightarrow \begin{cases} G_{\mathrm{dB}} \rightarrow G_0 - 20 \log x \\ \phi \rightarrow \mathrm{Arg}(-\dfrac{j\,H_0}{x}) = -\dfrac{\pi}{2} \end{cases}$
  
  on dit que la deuxième asymptote est une droite de pente -20 dB/décade pour le gain et $-\dfrac{\pi}{2}$ pour la phase ;
• Enfin, on remarque que les deux asymptotes du gain se croisent en $x = 1$.

Étude du gain

On a :

\begin{align} G_{\mathrm{dB}} &= 20 \log |\underline{H}(j\omega)| = 20 \log \left(\dfrac{H_0}{\sqrt{1+x^2}}\right) \\ & = 20 \log H_0 - 10 \log (1+x^2)\\ & = G_0 - 10 \log (1+x^2) \end{align}

On peut déjà noter que $G_{\mathrm{dB}}$ est une fonction décroissante pour $x \in \left[0,+\infty\right[$, et qu'elle est maximum pour $x=0$.

Il faut regarder une dernière chose avant de tracer le diagramme de Bode en gain : la courbe est-elle en dessous ou au dessus des asymptotes ?
Pour cela, trouvons le signe de :

• $G_{\mathrm{dB}} - G_0 = G_{\mathrm{dB}} = 20 \log \left(\dfrac{1}{\sqrt{1+x^2}}\right) < 0$
• $G_{\mathrm{dB}} - (G_0 - 20 \log x) = 20 \log \left(\dfrac{x}{\sqrt{1+x^2}}\right) < 0$

La courbe réelle sera donc toujours en dessous des asymptotes.

>Compléments : expliquons la provenance de ce -20 dB/décade

Calculons la valeur de l'asymptote d'équation $G_{\mathrm{dB}} = G_0 - 20 \log x$, pour deux valeurs de pulsation : $\omega_1$ et $\omega_2 = 10\, \omega_1$.

\begin{align} G_{\mathrm{dB}}(x_1) &= G_0 - 20 \log x_1\\ G_{\mathrm{dB}}(x_2) &= G_0 - 20 \log x_2 = G_0 - 20 \log x_1 - 20 \log 10\\ G_{\mathrm{dB}}(x_2) - G_{\mathrm{dB}}(x_1) &= -20\,\mathrm{dB} \end{align}

Ainsi, lorsque la pulsation est multipliée par 10 (une décade), le gain diminue de 20 dB.

Étude de la phase

La phase est égale à l'argument de la fonction de transfert complexe :

\begin{align} \phi(x) &= \mathrm{Arg}(\underline{H}(jx))= \mathrm{Arg}(H_0) - \mathrm{Arg}(1+jx) \\ \phi(x) &= - \arctan(x) \quad (\cos\,\phi > 0 \quad \text{car} \quad \mathcal{R}e(1+jx) = 1 > 0) \end{align}

En effet, on rappelle que la tangente d'un angle correspond à deux valeurs d'angle $\theta$ et $\pi - \theta$. Si le $\cos$ de l'angle est positif, on prend la première valeur.

On a trouvé précédemment le comportement asymptotique du déphasage :

• Lorsque $x \rightarrow 0$, $\phi(x) \rightarrow 0$ ;
• Lorsque $x \rightarrow \infty$, $\phi(x) \rightarrow -\pi/2$ ;
• Lorsque $x = 1$, $\phi = -\pi/4$.

On peut alors le diagramme de Bode en phase :

Étude d'un filtre passe-haut du premier ordre

En déroulant la même étude que précédemment sur le circuit suivant :

C'est à dire en intervertissant résistance et condensateur, on montre que celui-ci est un filtre passe haut du premier ordre.

En effet :

• Si $\omega \rightarrow 0$, $\underline{Z}_C \rightarrow \infty$ , condensateur $\Leftrightarrow$ interrupteur ouvert : $\underline{s}(t) =0$.
• Si $\omega \rightarrow \infty$, $\underline{Z}_C \rightarrow 0$ , condensateur $\Leftrightarrow$ interrupteur fermé : $\underline{s}(t) =\underline{e}(t)$. Les hautes fréquences sont conservées.

On obtient facilement la fonction de transfert suivante :

\begin{align} \underline{H}(jx) = H_0\,\dfrac{jx}{1+jx} \\ \text{avec} \quad H_0 = 1, \quad x=\dfrac{\omega}{\omega_C} \quad &\text{et} \quad \omega_C = \dfrac{1}{RC} \end{align}

Le gain est :

\begin{equation} \boxed{G_{\mathrm{dB}} = 20\,\log\left(\dfrac{x}{\sqrt{1+x^2}}\right)} \end{equation}

La phase est :

\begin{equation} \boxed{\phi(x) = \dfrac{\pi}{2}- \mathrm{arctan}\,x} \end{equation}

Remarque sur l'ordre des filtres

Si on souhaite davantage atténuer les hautes ou les basses fréquences avec des filtres passe-bas ou passe-haut, on peut utiliser des filtres du deuxième ordre : les pentes du gain seront en -40 dB/décade.

Filtres passe-bas et passe-haut : application, le filtre ADSL

A l'époque où les maisons conservaient leur ligne téléphonique classique, il fallait faire passer dans les fils téléphoniques les données du téléphone et les données d'internet. Pour cela, des bandes de fréquences distinctes étaient choisies :

• Le signal analogique du téléphone est affecté aux fréquences $[0, 4 \mathrm{kHz}]$;
• Le signal numérique d'internet aux fréquences [20 kHz, 1,1 MHz]

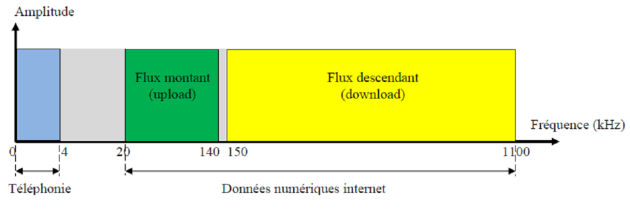
Il fallait donc placer un filtre ADSL sur la prise téléphonique murale, de ce filtre partait le câble permettant de relier la box internet, puis on plaçait sa prise téléphonique classique sur le filtre :

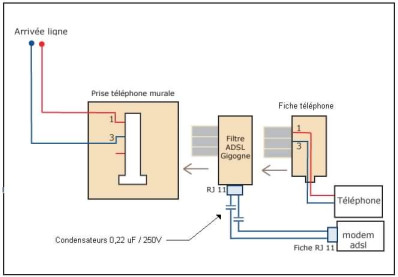
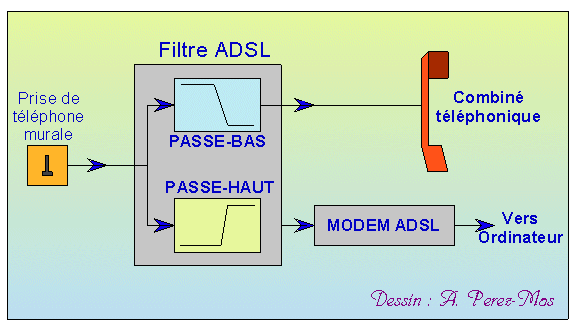
Le filtre ADSL est donc composé de deux filtres en parallèle, un filtre passe-bas permettant aux données téléphoniques de transiter, un filtre passe-haut qui sélectionne les fréquences dédiées à internet :

Etude d'un filtre passe-bande

Fonction de transfert

Un filtre passe-bande peut être construit à partir d'un circuit RLC série en prenant la tension aux bornes de la résistance :

Le diviseur de tension permet d'obtenir la fonction de transfert : le diviseur de tension (ou la loi des mailles) en régime sinusoïdal permet d'écrire :

\begin{equation} \underline{s}(t) = \dfrac{R}{R+j\,L\,\omega + \dfrac{1}{j\,C\,\omega}}\,\underline{e}(t) = \dfrac{1}{1 + j\,\dfrac{L}{R}\omega + \dfrac{1}{jRC\omega}}\,\underline{e}(t) \end{equation} \begin{equation} \text{d'où} \quad \underline{H}(j \omega) = \dfrac{1}{1+j \left(\dfrac{L\omega}{R}-\dfrac{1}{RC\omega}\right)} \end{equation}

La forme canonique s'obtient en faisant apparaître la fonction statique $H_0 = 1$, la pulsation réduite $x=\dfrac{\omega}{\omega_0}$ et on introduit une nouvelle grandeur appelé facteur de qualité $Q = \dfrac{1}{R}\sqrt{\dfrac{L}{C}}$.

On a alors $\dfrac{L}{R} = \dfrac{Q}{\omega_0}$ et $\dfrac{1}{RC} = Q\,\omega_0$. On obtient la fonction canonique suivante :

\begin{equation} \boxed{\underline{H}(jx) = \dfrac{H_0}{1+jQ \left(x - \dfrac{1}{x}\right)}} \end{equation}

Etude du gain

\begin{equation} \boxed{G_\mathrm{dB} = 20\,\log \dfrac{H_0}{\sqrt{1+Q^2\,\left(x-\dfrac{1}{x}\right)^2}}} \end{equation}

Etudions ces limites :

• Le gain est alors maximum pour $\left(x-\dfrac{1}{x}\right)^2 = 0$ soit $x=1 \Longleftrightarrow \omega=\omega_0$ et $G_\mathrm{dB\,max} = 0$;
• Si $x \rightarrow 0$ alors $G_\mathrm{dB} \rightarrow -\infty$;
• Si $x \rightarrow \infty $ alors $G_\mathrm{dB} \rightarrow -\infty$;

Etudions ces asymptotes :

• Si $x \ll 1$ alors $G_{\mathrm{dB}} \rightarrow 20\,\log\,x + 20\, \log\,\left(\dfrac{H_0}{Q}\right)$ : asymptote à +20 dB/décade;
• Si $x \gg 1$ alors $G_{\mathrm{dB}} \rightarrow -20\,\log\,x + 20\, \log\,\left(\dfrac{H_0}{Q}\right)$ : asymptote à -20 dB/décade;
• Les deux asymptotes se coupent en $\omega=\omega_0$ ($x=1$) pour une valeur de $G_{\mathrm{dB}} = 20\,\log\,\left(\dfrac{H_0}{Q}\right)$.
  Alors :
  • Si $Q < 1$, la courbe sera au dessus des asymptotes ($G_{\mathrm{dB}} = G_0 - 20\,\log\,Q$);
  • Si $Q > 1$, la courbe sera au dessous des asymptotes.

Pulsation de coupure et bande passante

On cherche les pulsations $\omega_1$ et $\omega_2$ qui vérifient $H(j\,\omega_1) = H(j\,\omega_2) = \dfrac{H_\mathrm{max}}{\sqrt{2}}$ :

\begin{equation} \dfrac{H_\mathrm{max}}{\sqrt{2}} = \dfrac{H_0}{\sqrt{1+Q^2\,\left(x-\dfrac{1}{x}\right)^2}} \Longleftrightarrow 1+Q^2\,\left(x-\dfrac{1}{x}\right)^2 = 2 \end{equation}

Soit :

\begin{equation} \left(x-\dfrac{1}{x}\right)^2 = \dfrac{1}{Q^2} \Longleftrightarrow \left[\left(x-\dfrac{1}{x}\right) + \dfrac{1}{Q}\right]\,\left[\left(x-\dfrac{1}{x}\right) - \dfrac{1}{Q}\right] = 0 \end{equation}

On a donc deux équations du second degré à résoudre. Voici la résolution de la première :

\begin{align} & \left(x-\dfrac{1}{x}\right) + \dfrac{1}{Q} = 0 \Longleftrightarrow x^2 + \dfrac{x}{Q} - 1 = 0 \\ & \Delta = \dfrac{1}{Q^2} - 4\times 1\times(-1) = 4\,\left(1+\dfrac{1}{4\,Q^2}\right) >0 \\ &x = -\dfrac{1}{2Q} \pm \sqrt{\left(1+\dfrac{1}{4\,Q^2}\right)} \quad \text{on ne peut garder que la solution positive} \end{align}

La résolution de la deuxième donne :

\begin{equation} x = \dfrac{1}{2Q} + \sqrt{\left(1+\dfrac{1}{4\,Q^2}\right)} \end{equation}

Les pulsations de coupure et donc la bande passante dépendent du facteur de qualité :

\begin{equation} \boxed{\omega_1 = \omega_0\,\left(-\dfrac{1}{2Q} + \sqrt{\left(1+\dfrac{1}{4\,Q^2}\right)}\right) \qquad \omega_2 = \omega_0\,\left(\dfrac{1}{2Q} + \sqrt{\left(1+\dfrac{1}{4\,Q^2}\right)}\right)} \end{equation} \begin{equation} \boxed{\Delta \omega = \omega_2 - \omega_1 = \dfrac{\omega_0}{Q}} \end{equation}

On voit que plus le facteur de qualité du filtre passe-bande est grand, plus le filtre est sélectif, la bande passante est plus petite.

Etude de la phase

\begin{equation} \phi = \mathrm{Arg}(\underline{H}(jx)) = \mathrm{Arg}\left(\dfrac{H_0}{1+jQ \left(x - \dfrac{1}{x}\right)}\right) = -\mathrm{Arg}\left(1 + jQ\,\left(x-\dfrac{1}{x}\right)\right) \quad \text{si } H_0 >0 \end{equation}

On peut étudier les limites de la phase à partir de la fonction de transfert. En effet :

\begin{equation} \begin{cases} \text{Si}\,x \rightarrow 0, \quad \underline{H}(jx) \simeq \dfrac{1}{j\,Q\,\left(-\dfrac{1}{x}\right)} = \dfrac{j}{Q}x \quad ; \quad \underline{H} \, \text{imaginaire pur >0} \, \Longrightarrow \phi = \dfrac{\pi}{2} \\ \text{Si}\,x \rightarrow \infty, \quad \underline{H}(jx) \simeq \dfrac{1}{j\,Q\,x} = \dfrac{-j}{Qx}\quad ; \quad \underline{H} \, \text{imaginaire pur < 0} \, \Longrightarrow \phi = -\dfrac{\pi}{2} \\ \quad \\ \text{Si}\,x=1, \quad \underline{H}(jx)=1 \Longrightarrow \phi = 0 \end{cases} \end{equation}

Etudions la tangente et le cosinus :

\begin{equation} \begin{cases} \tan\,(-\phi) = Q\,\left(x-\dfrac{1}{x}\right) \\ \cos\,(-\phi) = \cos\,\phi = \dfrac{1}{\sqrt{1+\left(Q\,\left(x-\dfrac{1}{x}\right)\right)^2}} > 0 \end{cases} \end{equation}

Finalement :

\begin{equation} \boxed{\phi(x) = -\mathrm{arctan}\left(Q \left(x-\dfrac{1}{x}\right)\right)} \end{equation}

Application : traitement de fichiers sonores

Dans le traitement du son, un filtre passe-bande permet de sélectionner une certaine bande de fréquences utiles, les autres étant atténuées.

Un logiciel, comme AVS audio editor, propose de traitement un son avec différents filtres, comme un filtre passe-bande : Filtre passe bande sous AVS Audio Editor.

On retrouve bien sûr ce type de filtres dans des logiciel libre type Audacity : l'effet wahwah de guitare est créé en utilisant un filtre passe-bande réglable ...

Références

• Fonction de transfert, filtrage :
  • http://physiquepcsimoreggia.hautetfort.com/media/00/01/1901656848.pdf
  • http://www.seigne.free.fr/Cours/AnaFourier.pdf>
• Transformée de Fourier et train d'onde : https://www.silicium628.fr/cours/tr_fourier/page3.php
• Fourier :
  • http://ressource.electron.free.fr/bts/cours/Signal.pdf
  • http://perso.univ-lemans.fr/~berger/Signal_MP2/TFourier/co/TFUsuelle.ht
  • https://www.youtube.com/watch?v=4XCSoFLFLNE
• Filtre ADSL : http://olivier.granier.free.fr/MOOC/co/filtrage-elec-ordre-1_1.html
• Wikipédia, diagramme de Bode et filtre passe-bande :
  • https://fr.wikipedia.org/wiki/Diagramme_de_Bode#Passe-haut
  • https://fr.wikipedia.org/wiki/Filtre_passe-bande
• Filtre passe-bande : http://mawy33.free.fr/cours%20sup/32-100%20%C3%A9l%C3%A9ctrocin%C3%A9tique%20RLC%20sinusoidal.pdf
• Filtres passifs : http://lyceehugobesancon.org/btssn/IMG/pdf/Filtres_passifs.pdf
• Lecture d'une courbe fréquentielle: https://www.lesnumeriques.com/audio/tuto-audio-comment-lire-courbe-reponse-frequentielle-a3561.html