flèche de retour

Physagreg

Cours de physique chimie

icone sommaireSommaire
icône cadeauBonus
icône chapitreAutres chapitres

Licence 1 > Thermodynamique > Cours 1 : grandeurs thermodynamiques et équations d'état

T2 : Transformations - premier principe

Introduction

La thermodynamique explore les transformations énergétiques dans les systèmes physiques. Dans ce chapitre après avoir abordé de façon générale la notion de transformation et exploré les différents adjectifs qu'on pourra associer à ce mot, nous verrons les processus qui permettent d'échanger de l'énergie entre notamment un système thermodynamique et l'extérieur : ce sont le travail et la chaleur. Pour cette dernière, on devra évoquer une de ses caractéristiques, la capacité calorifique. Pour ce qui est du travail, on s'intéressera au travail des forces de pression.
Enfin, le lien entre travail et chaleur donne naissance au premier principe de la thermodynamique, très utilisé dans la résolution des exercices quels qu'ils soient. On terminera par étudier la détente de Joule, une des nombreuses contribution de ce scientifique, ce qui permettra d'énoncé la première loi de Joule.

Transformations

Notion de transformation

Soit un corps dans un état d’équilibre appelé état 0 défini par $p_0$, $T_0$, $V_0$, on peut lui faire subir une transformation thermodynamique pour l’amener dans un état d’équilibre appelé état 1 défini par $p_1$, $T_1$, $V_1$.

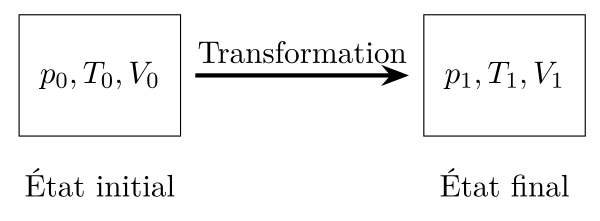
notion de transformation
Notion de transformation thermodynamique

Il est possible de représenter ces états dans un diagramme thermodynamique comme le diagramme de Clapeyron (pression=f(volume massique)), le diagramme de Watt (pression=f(volume)), le diagramme des frigoristes (pression=f(enthalpie)), etc.

«
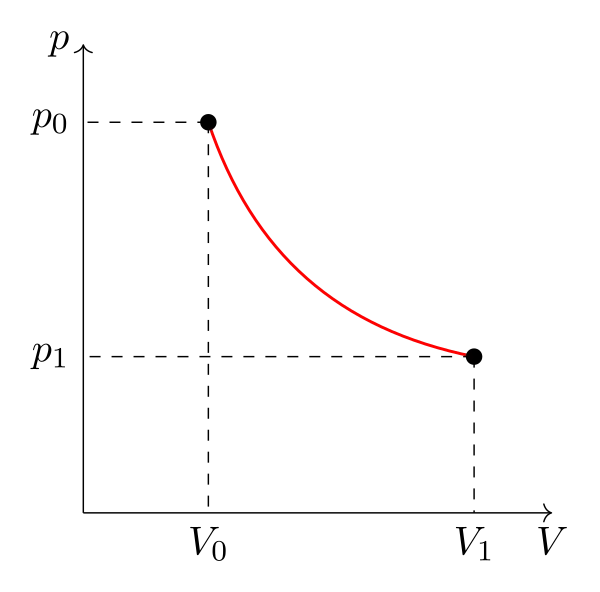
Exemple de diagramme de Watt entre l’état 0 et l’état 1

Transformation quasi-statique

Si, pour aller d’un état d’équilibre 0 à un état d’équilibre 1, le système passe par une succession d’état eux-même états d’équilibres, alors la transformation est dite quasi-statique.

Exemples :

Transformation réversible

Si en plus, pour une transformation quasi-statique, à chaque étape le système est en équilibre thermodynamique avec l’extérieur, alors la transformation est qualifiée de réversible.

Remarque : une transformation peut donc être quasi-statique sans être réversible mais si elle est réversible alors elle est nécessairement quasi-statique.

Des adjectifs pour des transformations particulières

Coefficients thermoélastiques

Remarque :
pour un gaz parfait, $V = \dfrac{n\,R\,T}{p} \Longrightarrow \dfrac{\partial V}{\partial T} = \dfrac{n\,R}{p} \Longrightarrow \alpha = \dfrac{1}{V}\,\dfrac{n\,R}{p} = \dfrac{1}{T}$

Chaleur et travail

Soit une casserole d’eau que l’on chauffe à l’aide d’une bougie, sa température augmente. Il s’avère que si on chauffe deux fois plus (avec deux bougies), alors la température s’élève deux fois plus. Cette expérience peut être interprétée par le fait que le système de chauffe a transmis de la chaleur à l’eau. On peut alors écrire que la quantité de chaleur transférée est proportionnelle à la température.

De la même manière, si on diminue la taille du système de moitié, une bougie suffit à élever la température deux fois plus que la situation avec système entier et une bougie. On peut donc écrire que la quantité de chaleur est inversement proportionnelle à la masse du système.

Enfin si on change de système, la relation entre quantité de chaleur et augmentation de la température change.

Capacités calorifiques

Dans de nombreuses situations, on peut donc écrire la proportionnalité entre la quantité de chaleur et la température \begin{equation}\delta Q = C\,\mathrm{d}T\end{equation} avec $C$ la capacité calorifique du système.

Si on considère que la capacité calorifique est indépendante de la température (ce qui est assez vrai) alors : \begin{equation}Q = C\,\Delta T\end{equation} On a donc une capacité calorique exprimée en $\mathrm{J.K^{-1}}$.

Remarque : différence pour une grandeur $G$ entre $\delta G$ et $\mathrm{d}G$

  • On note une grandeur infinitésimal $\delta G$ lorsqu’il ne s’agit pas d’une variation d’une grandeur d’état, que ce n’est pas une différentielle totale exacte, que son intégration entre deux états donnés dépend du chemin suivi.
  • Si la grandeur est notée $\mathrm{d}G$ alors il s’agit d’une différentielle totale exacte, son intégration entre deux états ne dépend que des caractéristiques de l’état initial et de l’état final et donc ne dépend pas du chemin suivi entre ces deux états.

La capacité calorifique peut être molaire ou massique, alors on définit :

Unité de la quantité de chaleur $Q$

Nous verrons par la suite l’équivalence entre travail et chaleur et ainsi que la chaleur est une quantité d’énergie qui s’exprime en Joule (J).

Une autre unité existe, issue de l’histoire des sciences et de la supposée existence du calorique, fluide qui passait d’un corps à un autre pour en changer sa température. La calorie est donc venue de cette histoire et on définit une calorie comme étant la quantité de chaleur à fournir à 1 g d’eau pour augmenter sa température d’1 sous pression atmosphérique. On admet que \begin{equation}1\,\mathrm{calorie} = 4,18\,\mathrm{J}\end{equation}

Signe des quantités d’énergie

Par convention, une quantité d’énergie reçue par un système est comptée positivement, une quantité d’énergie fournie à l’extérieur par le système est comptée négativement.

Capacité calorifique à pression constante ou volume constant

En thermodynamique, on effectue souvent des transformations :

Imaginons l’expérience où on réalise le chauffage d’une casserole d’eau en lui apportant une certaine quantité de chaleur. On réalise cette expérience :

Chauffage casserole fermée
Chauffage avec récipient fermé
Chauffage casserole ouverte
Chauffage avec récipient ouvert

L’élévation de température du système sera plus importante dans le premier cas: en effet pour une même quantité de chaleur apportée, celle-ci va servir :

On peut écrire pour ces deux expériences : \begin{equation}\delta Q = C_V\,\mathrm{d}T = C_p\,\mathrm{d}T'\end{equation} Or comme nous l’avons expliqué, $\mathrm{d}T > \mathrm{d}T'$, donc $C_V < C_p$.

Mesure de capacités calorifiques : calorimétrie

La calorimétrie est le domaine de la thermodynamique qui s’intéresse, entre autres, à la mesure de capacité calorifique de corps.

Exemple : on peut réaliser facilement une expérience visant à la mesure de la capacité calorifique d’un métal : dans un calorimètre, enceinte considérée comme adiabatique (pas d’échange de chaleur avec l’extérieur), on introduit :

Notons $Q_1$ la quantité de chaleur reçue par l’eau et le calorimètre : \begin{equation}Q_1 = (m+\mu)\,c_\mathrm{e}\,(T_f - T_1)\end{equation} Notons $Q_2$ la quantité de chaleur fournie par le métal : \begin{equation}Q_1 = M\,c_\mathrm{M}\,(T_f - T_M)\end{equation} L’enceinte (le calorimètre) étant adiabatique : \begin{equation}Q_1 + Q_2 = 0 \Longrightarrow \boxed{C_\mathrm{M} = \dfrac{-(m+\mu)\,c_e\,(T_f-T_1)}{M\,(T_f-T_M)}}\end{equation}

Remarque : Les expériences calorimétriques se faisant à pression constante (pression de l’atmosphère), calculer des quantités des chaleurs est équivalent à calculer des variations d’enthalpie. En cas de réaction chimique dans le calorimètre, on préfèrera utiliser les variations d’enthalpies plutôt que les quantités de chaleur et ainsi parler de variation d’enthalpie de réaction.

Notion de thermostat

Un thermostat est un système qui permet de conserver la température constante. Par exemple pour maintenir la température à 0°C, on peut utiliser un mélange eau+glace, ce mélange constitue le thermostat.

Travail

On connaît l’expression du travail mécanique, lorsqu’un corps se déplace et subit une force $\overrightarrow{F}$, on peut écrire :

\begin{equation}\delta W = \overrightarrow{F}\cdot \mathrm{d}\overrightarrow{OM} = \overrightarrow{F} \cdot \mathrm{d}\overrightarrow{\ell}\end{equation}

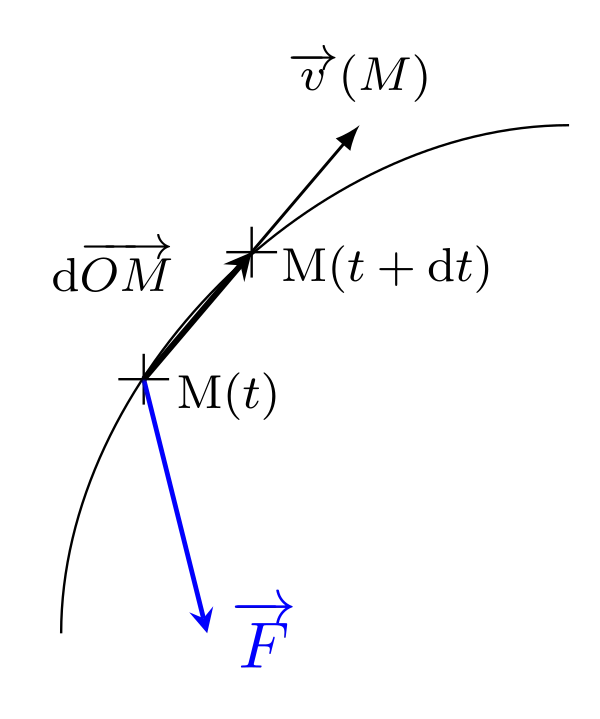
Travail mécanique
Expression du travail en mécanique

En thermodynamique, on s’intéresse très souvent aux forces de pression, imaginons la situation suivante :

Travail des forces de pression
Travail des forces de pression lors d’un déplacement du piston

Un gaz est contenu dans une enceinte munie d’un piston. Celui-ci est libre de se déplacer. La force que subit le gaz est la force exercée par la pression extérieure sur le piston. Soit : \begin{equation}F_\mathrm{ext} = p_\mathrm{ext} \times S\end{equation} où $S$ est la surface du piston.

On peut calculer le travail subit par le gaz pour un déplacement $\mathrm{d}\overrightarrow{\ell}$ du piston, qui est le travail de la force de pression extérieure sur le piston: \begin{equation}\delta W = \overrightarrow{F}_\mathrm{ext}\cdot \mathrm{d}\overrightarrow{\ell} = p_\mathrm{ext} \times S \,\mathrm{d}{\ell}\end{equation} puisque la force de pression et le déplacement élémentaire sont dans le même sens et la même direction. Or on reconnaît le produit $S \times \mathrm{d}\ell$ qui est la variation de volume du gaz de l’enceinte, et cette variation état négative : \begin{equation}\delta W = - p_\mathrm{ext}\,\mathrm{d}V\end{equation}

Si on est dans le cas d’une transformation quasi-statique c’est à dire que la transformation est par exemple suffisamment lente pour qu’à chaque instant il y ait équilibre thermodynamique entre l’extérieur et le gaz de l’enceinte, alors \begin{equation}\delta W = - p\,\mathrm{d}V\end{equation}

Ce travail élémentaire intégré entre deux états thermodynamiques peut se retrouver graphiquement dans un diagramme classique ($p$,$V$). En effet, il s’agit alors de l’aire sous la courbe :

Travail négatif et aire sous la courbe
Travail négatif et aire sous la courbe

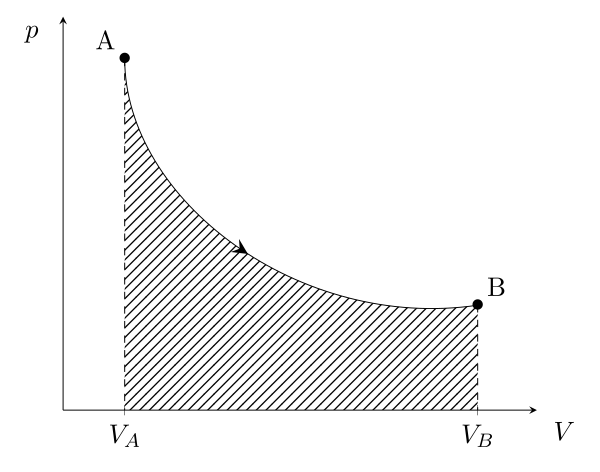
Dans ce premier cas, le volume du système grandi, c’est comme si celui-ci poussait l’atmosphère pour agrandir son volume donc le système fournit du travail \begin{equation}W_{A \to B} = -\int_A^B p\,\mathrm{d}V < 0\end{equation}

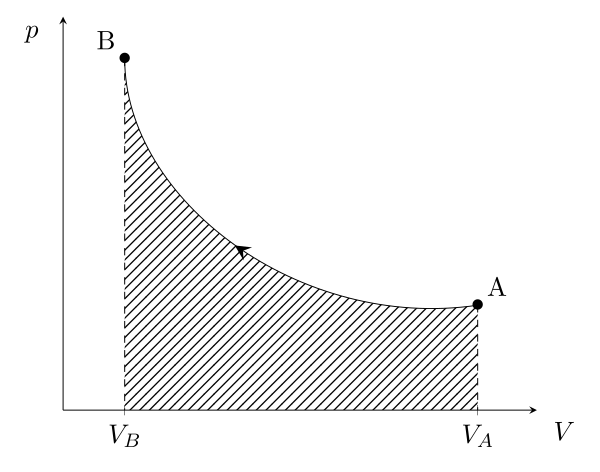
Travail positif et aire sous la courbe
Travail positif et aire sous la courbe

Dans ce deuxième cas, il y a diminution du volume, le système reçoit du travail \begin{equation}W_{A \to B} = -\int_A^B p\,\mathrm{d}V > 0\end{equation}

Premier principe de la thermodynamique

Equivalence entre travail et chaleur

Historiquement, ce sont les expériences de Joule qui ont montrées cette équivalence, il avait imaginé un dispositif ou le travail du à la chute d’un poids actionnait la rotation d’une hélice plongée dans un récipient d’eau : le frottement de celle-ci produisait de la chaleur. Il montre ainsi que le travail du poids est proportionnel à l’augmentation de température du liquide.

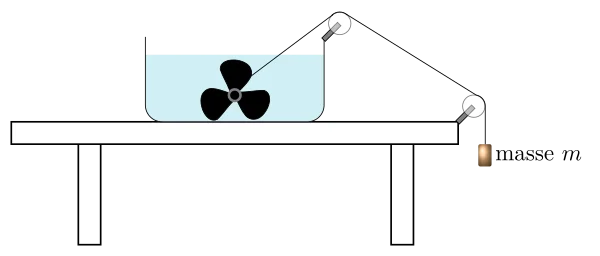
Expérience de Joule
Expérience de Joule

Sachant qu’avec l’expérience de la casserole d’eau chauffée par une bougie, on a vu précédemment que l’augmentation de température est proportionnelle à la chaleur apportée, alors travail et chaleur sont proportionnels, donc équivalent.

Notation : travail et chaleur ne sont pas des fonctions d’état

Nous avons vu précédemment que la quantité de chaleur et le travail élémentaire se notaient avec un $\delta$ à la place du $\mathrm{d}$ pour indiquer que ceux-ci dépendent du chemin suivi entre deux états, et pas seulement des caractéristiques de l’état initial et de l’état final de la transformation.

Ainsi, le transfert thermique et le travail ne sont pas des fonctions d’état.

Enoncé du premier principe de la thermodynamique

Pour une transformation élémentaire, on a \begin{equation}\delta Q + \delta W = \mathrm{d}U\end{equation}

Interprétation microscopique de l’énergie interne

Pour donner du sens à cette nouvelle grandeur physique appelée énergie interne, on peut en donner une signification microscopique : Soit un gaz parfait (pas d’interaction entre les molécules) comportant $N$ molécules, alors cette énergie est simplement la somme des énergies cinétiques de ces $N$ molécules \begin{equation}\boxed{U = \sum_{i=1}^N \dfrac{1}{2}\,m\,v_i^2}\end{equation}

Remarque : nous verrons plus loin dans ce cours de thermodynamique que les vitesses des molécules sont très diverses et qu’il convient d’introduire le concept de vitesse quadratique moyenne des molécules. On remplacera ainsi $\sum_{i=1}^{N} ... v_i^2$ dans l’expression de $U$.

Détente de Joule, première loi de Joule

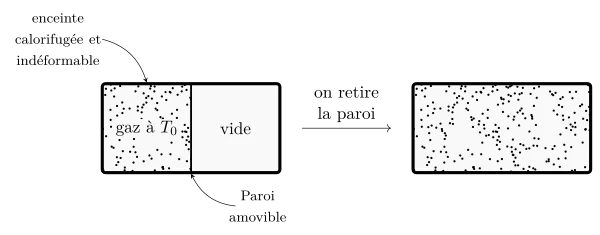
Détente de Joule
Détente de Joule

De plus, cette expérience réalisée avec un gaz parfait se fait sans changement de température : en effet, la température est liée à la vitesse des particules du gaz, et il n’y a aucune raison que les vitesses soient différentes du fait qu’il y ait plus d’espace disponible pour le gaz. Par contre la pression est modifiée : moins de chocs sur les parois car plus de volume disponible pour les molécule. Le volume change également puisqu’il est doublé.

Enthalpie

Expériences

On réalise simultanément les deux expériences suivantes, en apportant la même quantité de chaleur $\delta Q$ aux deux enceintes:

Expériences de chauffage sous deux conditions
Expériences de chauffage sous deux conditions et définition de l'enthalpie

On mesure l’augmentation de température dans les deux cas: la température va davantage augmenter dans le premier cas. En effet, calculons la variation d’énergie interne dans les deux cas:

En effet, comme $\mathrm{d}U = C_V\,\mathrm{d}T$ pour un gaz parfait, alors si $\mathrm{d}U_1 > \mathrm{d}U_2$ alors $\mathrm{d}T_1 > \mathrm{d}T_2$.

Ce résultat peut s’expliquer aisément si on regarde les conditions de la transformation dans les deux cas. Dans le deuxième cas, l’apport thermique permet à la fois d’augmenter la température du gaz de l’enceinte mais aussi d’augmenter le volume de celui-ci, le piston est poussé vers le haut, pousse l’atmosphère, donc fournit du travail. Tout l’apport énergétique ne sert pas uniquement à augmenter la température.

Définition

On a donc \begin{equation}\mathrm{d}H = \mathrm{d}U + \mathrm{d}(p\,V) = \mathrm{d}U + p\,\mathrm{d}V + V\,\mathrm{d}p\end{equation}

D’après ce que l’on a écrit dans la deuxième expérience ci-dessus \begin{equation}\mathrm{d}H = \delta Q - p\,\mathrm{d}V + p\,\mathrm{d}V + V\,\mathrm{d}p = \delta Q\end{equation} puisque à pression constante $\mathrm{d}p =0$.

Finalement, dans le cas d’une transformation monobare, c’est à dire lorsque la pression du gaz à l’état initial et à l’état final est la même et égale à la pression extérieure (cas de nombreuses réactions chimiques qui sont même des transformations isobares, à pression extérieures constantes)

L’enthalpie est une fonction plus "intéressante" que l’énergie interne puisqu’elle tient compte de la façon dont a été stockée l’énergie apportée, celle-ci n’est pas nécessairement apportée que pour fournir de l’énergie interne au gaz, elle a pu servir aussi à augmenter le volume de celui-ci, comme on vient de le voir.

Deuxième loi de Joule

Retour sur les capacités calorifiques

Avec les deux lois de Joule, on peut établir la relation entre la capacité calorifique à volume constant et la capacité calorifique à pression constante appelée relation de Mayer. En effet: \begin{equation}\begin{aligned} \mathrm{d}H &= \mathrm{d}U + \mathrm{d}(p\,V) \\ &= \mathrm{d}U + \mathrm{d}(n\,R\,T) \\ &= \mathrm{d}U + n\,R\,\mathrm{d}T \\ \Longleftrightarrow C_p\,\mathrm{d}T &= C_V\,\mathrm{d}T + n\,R\,\mathrm{d}T \\ \Longrightarrow C_p - C_V &= n\,R \end{aligned}\end{equation}

On peut alors introduire ici un coefficient qui intervient souvent en thermodynamique qui est le rapport $\gamma = \dfrac{C_p}{C_V}$, appelé coefficient adiabatique ou coefficient de Laplace, on peut alors exprimer $C_p$ et $C_V$, en fonction de celui-ci grâce à la relation de Mayer puisque \begin{equation}\dfrac{C_p-C_V}{C_V} = \dfrac{n\,R}{C_V} \Longrightarrow \gamma -1 = \dfrac{n\,R}{C_V} \Longrightarrow C_V = \dfrac{n\,R}{\gamma-1}\end{equation} Et aussi \begin{equation}\dfrac{C_p-C_V}{C_p} = \dfrac{n\,R}{C_p} \Longrightarrow 1-\dfrac{1}{\gamma} = \dfrac{n\,R}{C_p} \Longrightarrow C_p = \dfrac{\gamma\,n\,R}{\gamma-1}\end{equation}

Ce chapitre est l'occasion de donner les définitions générales des capacités calorifiques à volume constant et à pression constante, en fonction de l'énergie interne et de l'enthalpie:

Ressources :

Documents de référence

Derniers ajouts

Liens

Physique à l'ENSCR

physique àl'ENSCR

Retrouver, entre autres, des contenus de travaux pratiques, produits par l'équipe de physique de l'ENSCR