Licence 1 > Mécanique 1 > Cours 1 : chute libre

M11 : chute libre

Ce chapitre est disponible intégralement en vidéos. La première vidéo de la playlist dédiée est disponible ici :

Vous pouvez également visionner une vidéo particulière :

1. Introduction, référentiel, repère, base de projection
2. Vecteurs position, vitesse et accélération
3. Forces et lois de Newton
4. Chute verticale et chute parabolique, équations des mouvements
5. Chute parabolique : portée, flèche et dépendances

Introduction

Dans ce premier chapitre, l'étude d'un problème de chute libre va permettre de découvrir les bases de la mécanique du point.

Nous allons donc présenter tous les outils de la cinématique (description du mouvement d'un point) et de la dynamique (étude des causes du mouvement), qui permettent de connaître et de prévoir le mouvement d'un corps dans le modèle de la mécanique du point.

Après un problème de chute libre verticale, à une dimension, nous nous intéressons au mouvement d'un projectile, à deux dimensions.

Problème 1

Un objet, tenu immobile à $t<0$ à une hauteur $h$ du sol, et lâché à $t=0$ sans vitesse initiale.
Quel est son mouvement, les caractéristiques de celui-ci ?

Lorsque l'on traite un problème de mécanique, le système est la première des notions à préciser. Mais qu'est-ce qu'un système ?

Système et point matériel

Système

Le système est l'objet ou le groupe d'objet dont on souhaite étudier le mouvement.

La forme de l'objet nous importe donc peu puisque nous sommes dans le cadre de la mécanique du point. Ainsi, on choisira de suivre un point caractéristique du système : souvent son centre de gravité. Celui-ci pourra être repéré dans l'espace par la donnée de trois coordonnées.

Point matériel

Le point matériel est le point qui représente l'objet auquel on affecte toute la masse de l'objet considéré. Ce point, appelé souvent M et affecté de la masse $m$, est le point géométrique que l'on repère dans l'espace pour connaître son mouvement.

Pour notre problème

Le choix de notre système s'avère simple pour le problème On laisse chuter un objet, le point matériel M est le centre de gravité de cet objet affecté de la masse $m$ de l'objet.

Référentiel et base de projection

Voici la deuxième notion à définir pour un problème de mécanique : le référentiel.
Etudier le mouvement d'un objet ne veut rien dire si on ne définit pas par rapport à quoi on le décrit ? une valve de roue de vélo n'a pas le même mouvement que l'on observe celui-ci depuis la route, ou bien depuis le centre de la roue.
Nous devons donc définir précisément l'observateur du mouvement : c'est la notion de référentiel.

Référentiel

Définition

Choisir un référentiel c'est donc choisir le bon observateur pour le mouvement que l'on souhaite décrire. Ce référentiel est constitué d'un repère (une origine et trois axes) qui permette de repérer le point M dans l'espace et d'une horloge qui permet de mesurer de temps.
Rappelons que dans le cadre de la mécanique classique, le temps se mesure de la même manière dans tout référentiel, pour tout observateur.
Un référentiel sera généralement noté $\mathcal{R}$.

Choix d'un bon référentiel

Le mouvement dépendant du référentiel, il faut choisir le référentiel adéquat par rapport au mouvement que l'on souhaite étudier.
Souvent, on choisit parmi trois référentiels classiques dit galiléens (voir section sur les lois de Newton) :

• Le référentiel héliocentrique est un référentiel dont le centre du repère est situé au centre du soleil, et les trois axes du repère sont dirigés vers trois étoiles lointains considérés comme fixe ; il est utile pour étudier les mouvements des planètes du système solaire.
• Le référentiel géocentrique est un référentiel centré au centre de la Terre, ses trois axes sont dirigés vers les trois mêmes étoiles que celles du référentiel de héliocentrique; il est utilise pour étudier les mouvements de satellites terrestres par exemple ;
• Les référentiels terrestres sont des référentiels liés à des objets fixes à la surface de la Terre : lui est souvent associés un repère cartésien. Pour tous les mouvements qui se déroulent à la surface de la Terre, ce référentiel est approprié.

Base de projection, repère

Nous allons donc chercher à déterminer et décrire le mouvement du point matériel M de masse $m$. Pour cela, il faut pouvoir le repérer dans l'espace.

Définitions

On définit une base orthonormée directe qui sert au repérage :

• Ortho car les trois vecteurs de la base sont orthogonaux ;
• Normée car la norme des trois vecteurs de la base est égale à ;
• Directe signifie qu'elle respecte la règle du tire-bouchon : si on fait tourner le premier vecteur vers le deuxième, le tire-bouchon avance vers le troisième vecteur.

Les trois vecteurs définissent les trois directions dans lesquelles le point M pourrait se mouvoir.

Pour que le repérage dans l'espace du point M soit optimal, on ajoute une origine O à la base : l'ensemble d'une base et d'une origine constituent un repère.

Différentes bases pour différents problèmes

Nous verrons par la suite que plusieurs bases existent. Certaines sont fixes, d'autres mobiles. Ces bases sont appelées bases de projection, dans le sens où le traitement d'un problème de mécanique impose de projeter des grandeurs vectorielles (force, vecteur position, ...).
La base de projection doit être choisie de telle sorte qu'elle permette une résolution aisée du problème. Avec quelques habitudes, on sait laquelle est la plus judicieuse. Mais ce choix reste arbitraire : le résultat final est indépendant de la base choisie, mais un choix judicieux facilite souvent la résolution.

Il faut souligner ici la différence entre référentiel et base : on décrit le mouvement d'un corps par rapport à un référentiel, mais pour se faire, on peut choisir d'utiliser différentes bases. Comme nous le verrons, la vitesse d'un corps par rapport au référentiel choisi peut s'exprimer différemment dans plusieurs bases, les expressions étant toutes aussi valables les unes que les autres.

Exemple du repère cartésien

La base la plus classique est la base cartésienne qui définit un repère cartésien : autour d'une origine O sont définis trois vecteurs ($\overrightarrow{e}_x$, $\overrightarrow{e}_y$, $\overrightarrow{e}_z$) :

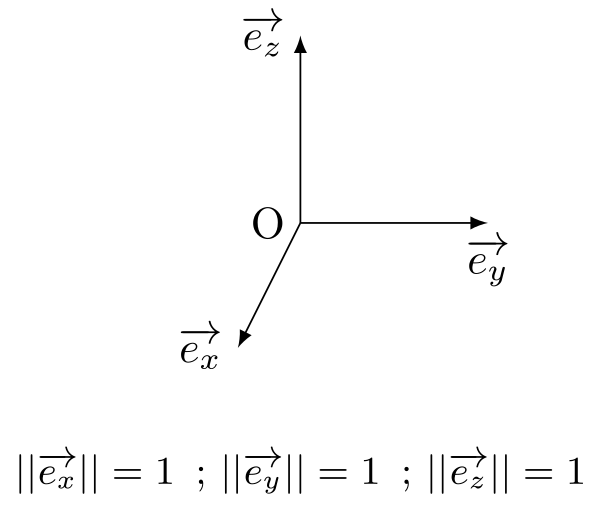
Cette base est fixe, la direction de chaque vecteur unitaire est constante.

Si on fait tourner le tire-bouchon de $\overrightarrow{e}_x$ vers $\overrightarrow{e}_y$, on se dirige vers le vecteur $\overrightarrow{e}_z$ ; Si on fait tourner le tire-bouchon de $\overrightarrow{e}_y$ vers $\overrightarrow{e}_z$, on se dirige vers le vecteur $\overrightarrow{e}_x$ ... C'est ainsi que la base est directe.

Système de coordonnées cartésiennes

Le point M sera repéré dans cette base cartésienne par trois coordonnées, une position de M dans cette base sera notée M($x$,$y$,$z$).

Pour notre problème

Notre premier problème étant à une dimension, on choisira comme axe de travail un des axes du repère cartésien. Pour un mouvement vertical, on utilise généralement la direction donnée par $\overrightarrow{e}_z$ : l'axe est donc vertical ascendant.

Vecteurs position, vitesse et accélération

Une fois, référentiel et base choisis, on peut exprimer les différents vecteurs qui nous permettent de décrire le mouvement du point M. Voici ces vecteurs.

Vecteur position

Définition

Le vecteur position noté $\overrightarrow{\mathrm{OM}}$ est le vecteur qui permet de repérer le point M dans l'espace. Celui-ci, comme tout vecteur possède quatre caractéristiques :

• Un point d'application : ici le point O, point fixe du référentiel qui sera souvent l'origine du repère choisi ;
• Une direction : celui de la droite OM ;
• Un sens : dirigée de O vers M ;
• Une norme : elle sera noté $||\overrightarrow{\mathrm{OM}}||$, nous verrons son expression mathématique en fonction du système de coordonnées.

Dans le système cartésien

Dans un repère cartésien (O,$x$,$y$,$z$), le point M possède trois coordonnées ($x$,$y$,$z$) suivant les axes O$x$, O$y$ et O$z$.
Le vecteur position s'exprime alors de la manière suivante : \begin{equation} \overrightarrow{\mathrm{OM}} = x\,\overrightarrow{e}_x + y\,\overrightarrow{e}_y + z\,\overrightarrow{e}_z \end{equation}

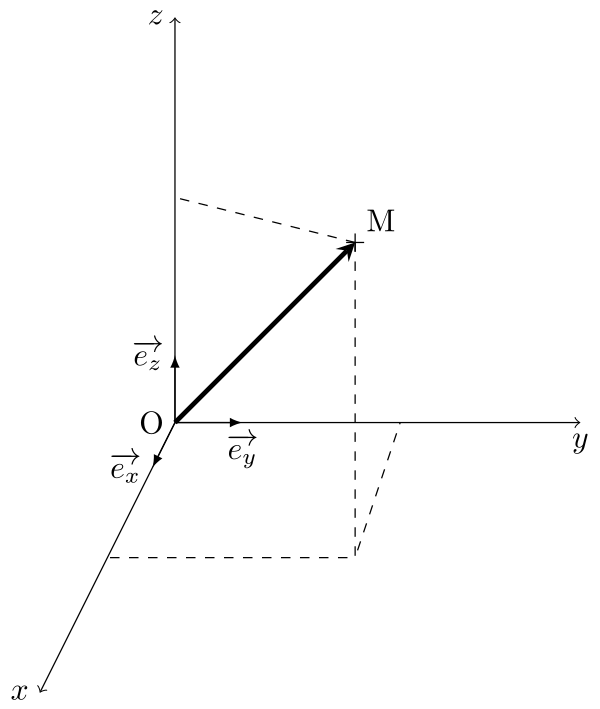
Dans le cas de notre problème

Le problème est à une dimension, comme nous l'avons dit précédemment, nous utiliserons l'axe vertical Oz, et le vecteur position s'écrit : $\overrightarrow{OM}=z\,\overrightarrow{e}_z$.

Vecteur vitesse

Définition

Soit un point M se déplaçant pendant le temps $\Delta t$ de la position $\overrightarrow{\mathrm{OM}}(t)$ à la position $\overrightarrow{\mathrm{OM}}(t+\Delta t)$.

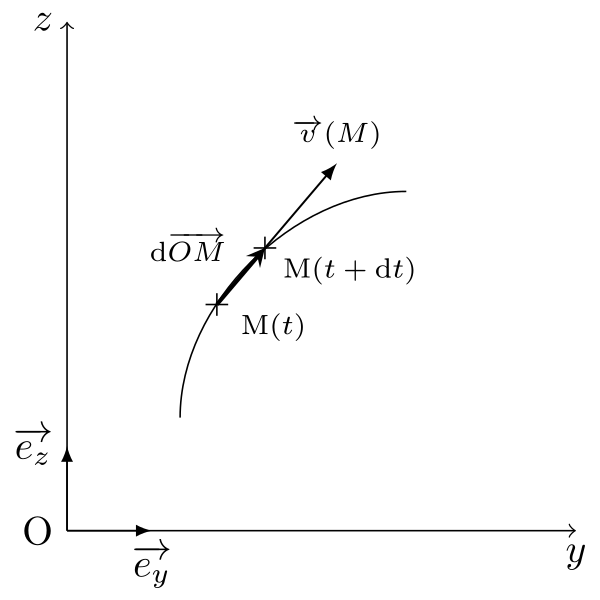
Par définition, le vecteur vitesse vaut :

\begin{equation} \overrightarrow{v}(M) = \lim_{\Delta t\rightarrow 0} \dfrac{\overrightarrow{\mathrm{M}(t)\mathrm{M}(t+\Delta t)}}{\Delta t} = \lim_{\Delta t\rightarrow 0}\dfrac{\overrightarrow{\mathrm{OM}}(t+\Delta t) - \overrightarrow{\mathrm{OM}}(t)}{\Delta t} = \dfrac{\mathrm{d}\overrightarrow{\mathrm{OM}}}{\mathrm{d}t} \end{equation}

Deux conséquences de cette relation :

• le vecteur vitesse est tangent à la trajectoire ;
• la norme du vecteur vitesse est égale au coefficient directeur de la tangente à la courbe $OM=f(t)$ au point considéré.

D'après cette définition, on sait également que pour passer du vecteur vitesse au vecteur position, il faut intégrer sans oublier la constante d'intégration.

Notion de déplacement élémentaire

Le vecteur $\mathrm{d}\overrightarrow{OM}$ est appelé déplacement élémentaire de M, c'est le déplacement de M pendant un temps infinitésimal $\mathrm{d}t$. Il se note parfois $\mathrm{d}\overrightarrow{\ell}$. Cette notion est importante, nous la retrouverons souvent en physique.
Le vecteur vitesse en un point M est donc la vitesse du point lors d'un déplacement élémentaire qui a lieu pendant un temps infinitésimal.

Vecteur vitesse et référentiel

Etant donné que la vitesse dépend du référentiel, il faut théoriquement préciser dans quel référentiel on dérive le vecteur position : on écrit $\overrightarrow{v}(M)_{/\mathcal{R}} = \left(\dfrac{\mathrm{d}\overrightarrow{\mathrm{OM}}}{\mathrm{d}t}\right)_{/\mathcal{R}}$

Seulement, cette notation est lourde, et nous repèrerons aisément les exercices où il sera nécessaire de préciser le référentiel.
Ainsi, à part dans le chapitre changement de référentiel, on omettra la précision du référentiel.

Vecteur vitesse et base de projection

L'expression du vecteur position $\overrightarrow{\mathrm{OM}}$ dépend de la base de projection choisie. Il faut en avoir conscience lorsque l'on calcule le vecteur vitesse.
En effet, en base cartésienne, on a : \begin{equation} \overrightarrow{\mathrm{OM}} = x\,\overrightarrow{e}_x + y\,\overrightarrow{e}_y + z\,\overrightarrow{e}_z \end{equation}
Donc :
\begin{align} \overrightarrow{v}(M) &= \dfrac{\mathrm{d}\overrightarrow{\mathrm{OM}}}{\mathrm{d}t} = \dfrac{\mathrm{d}x}{\mathrm{d}t}\times\overrightarrow{e}_x + x\times\dfrac{\mathrm{d}\overrightarrow{e}_x}{\mathrm{d}t} + \dfrac{\mathrm{d}y}{\mathrm{d}t}\times\overrightarrow{e}_y + y\times\dfrac{\mathrm{d}\overrightarrow{e}_y}{\mathrm{d}t} +\dfrac{\mathrm{d}z}{\mathrm{d}t}\times\overrightarrow{e}_z + z\times\dfrac{\mathrm{d}\overrightarrow{e}_z}{\mathrm{d}t} \end{align} Comme la base de projection cartésienne est fixe dans le référentiel choisi, on a $\dfrac{\mathrm{d}\overrightarrow{e_i}}{\mathrm{d}t} = \overrightarrow{0}$. Et finalement : \begin{equation} \overrightarrow{v}(M) = \dot{x}\,\overrightarrow{e}_x + \dot{y}\,\overrightarrow{e}_y + \dot{z}\,\overrightarrow{e}_z \end{equation} On rappelle que $\dot{x} = \dfrac{\mathrm{d}x}{\mathrm{d}t}$.

Mais attention, certaines bases de projection sont mobiles, il faudra en tenir compte pour le calcul du vecteur vitesse.

Cas de notre problème

D'après ce qu'il vient d'être dit, $\overrightarrow{v}(M) = \dot{z}\,\overrightarrow{e}_z$.

Notion de vitesse algébrique

Dans le cas d'un vecteur vitesse qui n'a qu'une seule composante, on pourra rencontrer la notation suivante :
\begin{equation} \overrightarrow{v}(M) = v\,\overrightarrow{u} \end{equation} Où $\overrightarrow{u}$ est un vecteur unitaire ($\overrightarrow{e}_x, \overrightarrow{e}_y\,\text{ou}\,\overrightarrow{e}_z$ par exemple).
Dans ce cas, $v$ est la vitesse algébrique, ce qui signifie que $v$ peut être positive ou négative :

• Si $v$ est positive, alors le point M va effectivement dans le sens du vecteur unitaire $\overrightarrow{u}$ ;
• Si $v$ est négative, alors le point M va dans le sens inverse du vecteur unitaire $\overrightarrow{u}$.

Vecteur accélération

Définition

Par définition :
\begin{equation} \overrightarrow{a}(M) = \dfrac{\mathrm{d}\overrightarrow{v}(M)}{\mathrm{d}t} = \dfrac{\mathrm{d}^2 \overrightarrow{\mathrm{OM}}}{\mathrm{d}t^2} \end{equation}

Ainsi pour passer du vecteur accélération au vecteur vitesse, il faudra intégrer une fois (sans oublier la constante d'intégration), pour passer du vecteur accélération au vecteur position, il faudra intégrer deux fois (avec l'apparition de deux constantes d'intégration).

En coordonnées cartésiennes

La base de projection cartésienne étant toujours fixe, seules les coordonnées $(x,y,z)$ sont dérivées : \begin{equation} \overrightarrow{a}(M) = \ddot{x}\,\overrightarrow{e}_x + \ddot{y}\,\overrightarrow{e}_y + \ddot{z}\,\overrightarrow{e}_z \end{equation}

Cas de notre problème

On a $\overrightarrow{a}(M) = \ddot{z}\,\overrightarrow{e}_z$.

Forces

Voilà le troisième volet de ce qu'il est essentiel de préciser lorsque l'on s'attaque à un problème de mécanique.
Il convient d'effectuer un bilan des forces qui s'exercent sur le système matériel dont on a choisi d'étudier le mouvement : on essaiera le plus souvent de réaliser un schéma montrant les forces sur le système.

Définition

Une force est un objet mathématique, un vecteur, qui permet de modéliser une action mécanique. Cette action provoque le mouvement du système, modifie ce mouvement ou créé une déformation du système.
Comme tout vecteur, on rappelle ses quatre caractéristiques :

• Un point d'application ;
• Une direction ;
• Un sens ;
• Une norme.

Différents types d'action

Ces deux types d'action sont à opposer : s'il y a contact physique entre le système mécanique et un solide ou un fluide qui provoque l'action, on parle d'action de contact ; sinon, il s'agit d'une action à distance.

Les actions de contact

La tension d'un fil ou celle d'un ressort sont des actions de ce type. La réaction d'un support aussi.

La force de frottement fluide est également une force qui modélise une action de contact.

Les actions à distance

Comme leur nom l'indique, ces actions mécaniques ont lieues sans contact physique entre le système matériel et le corps qui provoque l'action.
Les exemples les plus classiques, sont la force électrique, la force magnétique ou la force d'interaction gravitationnelle créées par des champs.
Ainsi toutes les quatre interactions fondamentales sont des actions à distance, puisque l'interaction faible et forte sont aussi des actions à distance.

Cas du problème 1

Deux situations distinctes peuvent être distinguées, ce qui nous permet de rencontrer les deux types d'action mécanique :

• Dans le cas où l'objet est dans sa position initiale, il est tenu et subit deux actions :
  • Une action de contact de la part de la main qui tient l'objet. Cette action est modélisée par la force de réaction $\overrightarrow{R}=\overrightarrow{F}_{M/O}$ ;
  • Une action à distance, l'attraction gravitationnelle de la Terre sur l'objet, modélisée par la force poids $\overrightarrow{P} = \overrightarrow{F}_{T/O}$.

Remarquons que nous avons représenté les deux forces avec le même point d'application, c'est à dire le centre d'inertie de l'objet, mais rappelons que nous sommes dans le cadre de la mécanique du point, il n'y a pas réellement de centre d'inertie puisque notre objet est ponctuel.

• Dans le cas où l'objet est en chute libre, il ne subit que l'action mécanique à distance exercée par la terre sur lui, modélisée par la force poids, $\overrightarrow{P}=\overrightarrow{F}_{T/O}$.

Lois de Newton

Souvent, les problèmes simples de mécanique se résolvent à l'aide de la deuxième loi de Newton appelée principe ou relation fondamentale de la dynamique.
Dans tous les cas, le quatrième point que l'on précise lorsqu'on traite un problème de mécanique est le nom du théorème utilisé pour la résolution.

Avant de présenter le PFD, parlons des deux autres lois de Newton.

1^ère loi de newton : principe d'inertie

Définition

"Tout corps persévère dans son immobilité ou son mouvement rectiligne uniforme (en ligne droite à vitesse constante) si les forces qui s'exercent sur lui se compensent".

Cette première loi, contenue dans la deuxième loi de newton, permet de savoir si le mouvement de l'objet est simple, par l'étude des forces. Il n'y a pas de traitement mathématique à faire. Elle permet une première approche du mouvement de l'objet.

L'immobilité et le mouvement rectiligne uniforme se distingue en fonction de l'existence d'une vitesse initiale.

Un corps sur lequel s'exercent des forces qui se compensent est appelé corps pseudo-isolé. Un corps isolé n'existe pas : il faudrait qu'il n'y ait aucune force à s'exercer sur lui.

Cas du problème 1

Utilisons la première loi de Newton dans les deux situations du problème évoquées précédemment :

• Dans la situation initiale, deux forces s'exercent sur notre objet, elles se compensent (même direction, même norme, sens opposé) : le principe d'inertie est vérifié. Comme l'objet n'a pas de vitesse initialement, il reste immobile.
• Une fois lâché, l'objet est en chute libre puisqu'il n'est soumis qu'à son poids. Cette force ne peut pas être compensée, le principe d'inertie n'est pas vérifié, l'objet n'est pas immobile, son mouvement n'est pas rectiligne uniforme.

3^ème loi de newton : principe des actions réciproques

Définition

Soit deux corps A et B qui exercent mutuellement une force sur l'autre corps. Alors on a :
$\overrightarrow{F}_{A/B} = - \overrightarrow{F}_{B/A}$
Les forces sont donc de même direction, de même norme et de sens différents

Attention, ces deux forces ne s'exercent pas sur le même système matériel ! dans un bilan de force sur un système dont on étudie le mouvement, elles ne peuvent pas apparaître toutes les deux.

Cas du problème 1

Prenons le cas de la situation initiale du problème, lorsque l'objet est immobile dans la main.

Si la main exerce une force $\overrightarrow{F}_{M/O}$ sur l'objet, alors l'objet exerce une force $\overrightarrow{F}_{O/M}= -\overrightarrow{F}_{M/O}$ sur la main.

De la même manière, si la Terre exerce une force $\overrightarrow{F}_{T/O}$ sur l'objet, alors l'objet exerce une force $\overrightarrow{F}_{O/T} = - \overrightarrow{F}_{T/O}$ sur la Terre.

2^ème loi de newton : principe ou relation fondamentale de la dynamique

Notion de quantité de mouvement

Soit un système matériel de masse $m$, de vitesse par rapport au référentiel choisi $\overrightarrow{v}$, alors la quantité de mouvement de ce système est :
\begin{equation} \boxed{\overrightarrow{p} = m\,\overrightarrow{v}} \end{equation}
La masse s'exprime en kilogramme (kg), la vitesse en mètre par seconde ($\mathrm{m.s^{-}}$), la quantité de mouvement s'exprime donc en kilogramme fois mètre par seconde ($\mathrm{kg.m.s^{-1}}$).

Expression de la loi

• seules les forces extérieures au système matériel sont prises en compte dans cette loi, d'où l'intérêt de bien définir l'étendue du système dés le début du problème ;
• dans la plupart de nos problèmes de mécanique, la masse du système considéré est constante si bien que le PFD peut être écrit :
  \begin{equation} m\,\dfrac{\mathrm{d}\overrightarrow{v}}{\mathrm{d}t} = \boxed{m\, \overrightarrow{a} = \sum \overrightarrow{F}_{\mathrm{ext}}} \end{equation}

Cas du problème 1

Reprenons une nouvelle fois nos deux situations :

• Dans un premier temps, l'objet est soumis à deux forces qui se compensent, celle de la main et celle de la Terre.
  Si on applique le PFD, on a :
  \begin{equation} m\,\dfrac{\mathrm{d}\overrightarrow{v}}{\mathrm{d}t} = \sum \overrightarrow{F}_{\mathrm{ext}} = \overrightarrow{0} \Longleftrightarrow \dfrac{\mathrm{d}\overrightarrow{v}}{\mathrm{d}t} = \overrightarrow{0} \Longleftrightarrow \overrightarrow{v} =\overrightarrow{\mathrm{cste}} \end{equation}
  Comme la vitesse initiale est nulle, l'objet reste sans vitesse, immobile : on retrouve le principe d'inertie.
  
  
• Dans le second temps, l'objet n'est plus soumis qu'à son poids, on peut donc écrire : \begin{equation} m\,\overrightarrow{a} = m\,\overrightarrow{g} \Longleftrightarrow \overrightarrow{a} = \overrightarrow{g} \end{equation} Ainsi, on sait que l'accélération est constante et égale à l'accélération de la pesanteur.

Equations du mouvement de l'objet du problème 1

C'est en projetant la deuxième loi de Newton sur la base de projection choisie (on s'affranchit alors des vecteurs), et en réalisant quelques intégrations que nous avons accès aux équations du mouvement.

Accélération

Le principe fondamental de la dynamique, $\overrightarrow{a} = \overrightarrow{g}$, projeté sur la base cartésienne choisie (l'axe Oz vertical ascendant) nous donne l'expression de l'accélération :
\begin{equation} a_z = \ddot{z} = -g \end{equation} L'accélération est constante (elle n'est pas fonction du temps), le mouvement ne se fait que selon une direction, ce mouvement est dit rectiligne uniformément accéléré.

Vitesse

Intégration

A partir de l'équation de l'accélération, on obtient la vitesse en primitivant. Il ne faut pas alors oublier la constante d'intégration :
\begin{equation} v_z(t) = \dot z(t) = -g\,t + \mathrm{cste} \end{equation} Remarque
On a écrit $v(t)$ puisque nous voyons bien que la vitesse contrairement à l'accélération est fonction du temps.

Détermination de la constante

La constante s'obtient à partir de la condition initiale sur la vitesse : dans l'énoncé du problème, nous avons dit que l'objet était lâché sans vitesse initiale, ce qui signifie que $v(t=0) = 0$. Ainsi : \begin{equation} v_z(t=0) = -g\times 0 + \mathrm{cste_1} \Longleftrightarrow \mathrm{cste_1} = 0 \end{equation} Et finalement : \begin{equation} \boxed{v_z(t) = -g\,t} \end{equation}

Vitesse négative ?

Position

Intégration

La position s'obtient à partir de la vitesse, en intégrant celle-ci : \begin{equation} z(t) = -\frac{1}{2}\,g\,t^2 + \mathrm{cste_2} \end{equation}

Détermination de la constante

On utilise cette fois la condition initiale sur la position : l'objet est lâchée d'une hauteur $h$, donc : \begin{equation} z(t=0) = h = -\frac{1}{2}\,g\times 0 + \mathrm{cste_2} \Longleftrightarrow \mathrm{cste_2} = h \end{equation} Et finalement : \begin{equation} \boxed{z(t) = -\frac{1}{2}\,g\,t^2 + h} \end{equation}

Caractéristiques du mouvement

Durée de chute

Reprenons l'expression de la position en fonction du temps : \begin{equation} z(t) = -\frac{1}{2}\,g\,t^2 + h \end{equation} La chute se termine lorsque l'objet arrive au sol, soit quand $z(t) =0$. On peut alors calculer la durée $T$ de la chute : \begin{equation} 0 = -\frac{1}{2}\,g\,T^2 + h \Longleftrightarrow \boxed{T = \sqrt{\dfrac{2\,h}{g}}} \end{equation}
Application
Un objet chute d'une hauteur de $10\,\mathrm{m}$, combien de temps dure sa chute :
\begin{equation} T = \sqrt{\dfrac{2\times 0,1}{10}} = 1,4\,\mathrm{s} \end{equation} Bien entendu, inutile de préciser la masse de l'objet qui chute ...

Vitesse au sol

Problème n°2

Trajectoire d’un tir : on lance un projectile dans le champ de pesanteur terrestre : quel est son mouvement, les caractéristiques de celui-ci ?
Conditions initiales : $z(t=0)=h$ ; $v(t=0)=v_0\,\cos\,\alpha\,\overrightarrow{uy}+v_0\,\sin\,\alpha\,\overrightarrow{uz}$.

Résolution du problème n°2

Système

Le système est le projectile de masse $m$, considéré comme ponctuel.

Référentiel et base

On utilise un référentiel terrestre (lié à un objet posé sur Terre) supposé galiléen.

On utiliserons une nouvelle fois une base cartésienne liée au référentiel terrestre, mais cette fois-ci, on travaille à deux dimensions. On choisira un axe horizontal dirigé vers la droite Oy et un axe vertical ascendant Oz :

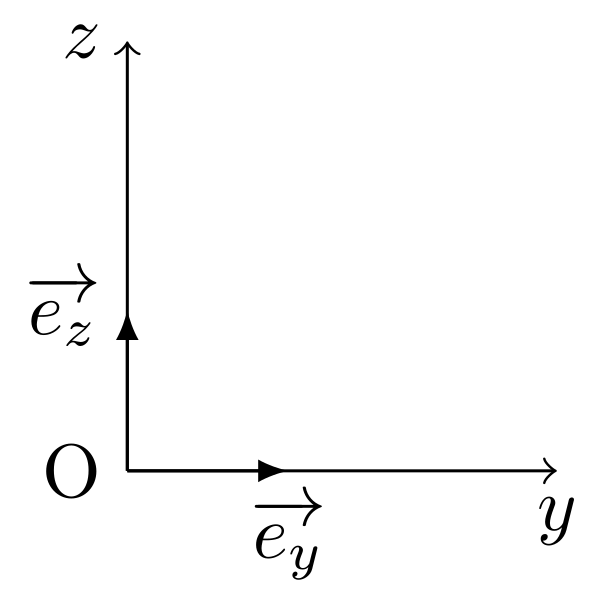
Bilan des forces et schématisation

A $t > 0$, la seule force qui s'exerce sur le projectile est son poids, force de la Terre sur le projectile.

On peut schématiser la situation en incluant les conditions initiales :

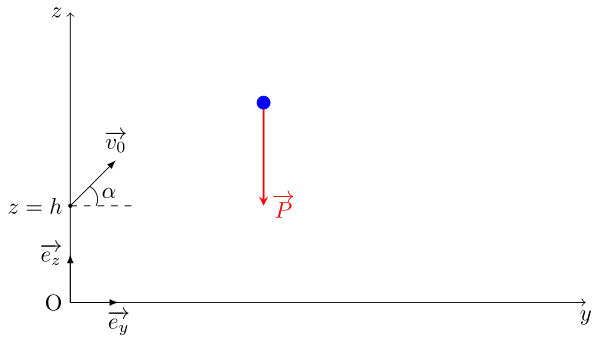
Théorème : deuxième loi de Newton et ses projections

Comme pour le problème n°2, la deuxième loi de Newton donne : $\overrightarrow{a} = \overrightarrow{g}$.
On peut projeter celle-ci sur les deux axes de la base choisie :

Or à $t=0$, on a $v_{0y} = v_0\,\cos\,\alpha = \mathrm{cste_1}$ et $v_{0z} = v_0\,\sin\,\alpha = \mathrm{cste_2}$, donc :

Or à $t=0$, on a $y(t=0) = 0 = \mathrm{cste_3}$ et $z(t=0) = h = \mathrm{cste_4}$, donc :

\begin{equation} \left|\begin{array}{l} \text{sur Oy : } \boxed{y(t) = (v_0\,\cos\,\alpha)\,t}\\ \text{sur Oz : } \boxed{z(t) = -\frac{1}{2}\,g\,t^2 + (v_0\,\sin\,\alpha)\,t + h} \end{array}\right. \end{equation}

Equation de la trajectoire

Cette équation va nous permettre de tracer la fonction mathématique dans le repère yOz. Ainsi, on cherche à obtenir la fonction $z(y)$.
Ainsi à partir de l'expression de $y(t)$ obtenue précédemment, on exprime $t$ :

On remplace cette expression de $t$ dans l'équation $z(t)$ :

L'équation de la trajectoire est donc :

En traçant cette fonction $z(y)$, nous nous apercevons que le mouvement est parabolique :

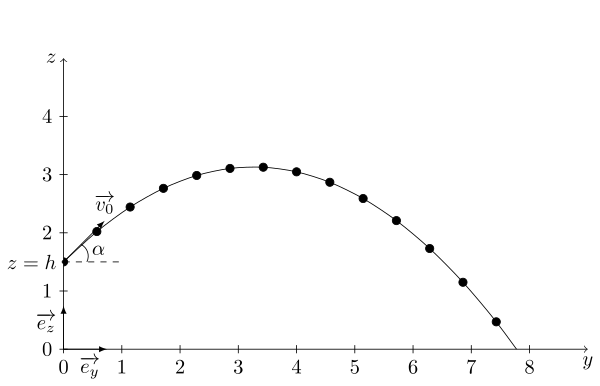
En effet, la fonction mathématique $z(y)$ définie une parabole.

Portée

On appelle portée la distance horizontale maximale atteinte par le projectile.
Pour la trouver, on utilise l'équation de la trajectoire, on cherche les solutions de l'équation $z=0$ (le projectile touche le sol).

\begin{equation} z = 0 \Longleftrightarrow -\dfrac{1}{2}\,g\,\dfrac{y^2}{v_0^2\,\cos^2\,\alpha} + y\,\tan\,\alpha + h = 0 \end{equation}

On obtient une équation du second degré dont la solution positive est la portée.
Avec les conditions initiales du problème n°2 ($v_0 = 8\,\mathrm{m.s^{-}}$, $\alpha = 45^{\circ}$ et $h = 1,5\,\mathrm{m}$), on trouve une portée de $7,79\,\mathrm{m}$.

Paramètres qui influencent la portée

La vitesse initiale modifie la trajectoire donc la portée, plus cette vitesse est importante pour un angle et une hauteur donnée, plus la portée sera grande.

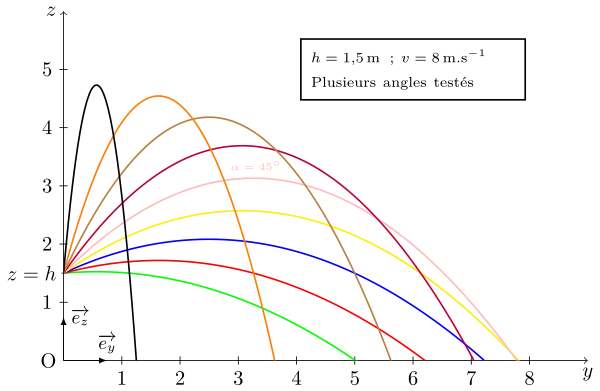
La hauteur de départ à également une influence sur la portée :

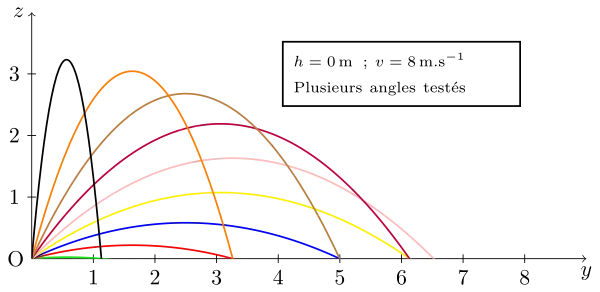
Enfin l'angle de départ à une influence sur la valeur de la portée :

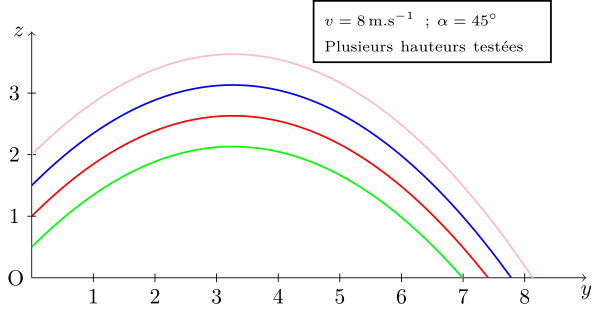
Nous voyons sur cette dernière figure que la portée n'est pas maximale, dans ces conditions, pour un angle de 45°.

Un cas plus simple

Portée maximale pour 45°

En effet, La portée est maximale pour un angle de 45° dans le cas où l'altitude de départ égale à l'altitude d'arrivée comme le montre la figure suivante.

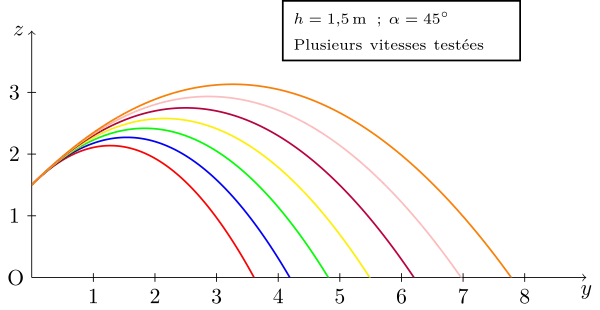
Car dans ce cas, l'équation du second degré qui donne la valeur de la portée se simplifie :

\begin{align} \text{Si } h=0 \text{, alors } &-\dfrac{1}{2}\,g\,\dfrac{y^2}{v_0^2\,\cos^2\,\alpha} + y\,\tan\,\alpha = 0 \\ \Longleftrightarrow & y\, \left(-\dfrac{1}{2}\,g\,\dfrac{y}{v_0^2\,\cos^2\,\alpha} + \tan\,\alpha\right) = 0 \end{align}

On a alors deux solutions, soit $y=0$, qui correspond à la position initiale et qui n'a pas d'intérêt ; soit :

\begin{align} -\dfrac{1}{2}\,g\,\dfrac{y}{v_0^2\,\cos^2\,\alpha} + \tan\alpha = 0 &\Longleftrightarrow y = \dfrac{2\,\tan\alpha\,v_0^2\,\cos^2\alpha}{g} = \dfrac{2\,v_0^2\,\sin \alpha \cos \alpha}{g} \\ &\Longleftrightarrow \boxed{y = \dfrac{v_0^2\,\sin 2 \alpha}{g}} \end{align}

En utilisant la formule de trigonométrie : $\sin 2\,\alpha = 2\sin \alpha \cos \alpha$.

On retrouve bien que cette portée est maximale lorsque l'argument du sinus vaut $\pi/2$ donc lorsque l'angle $\alpha$ vaut $45^\circ$.

Deux angles pour la même portée

On voit également sur la figure 2, que deux angles conduisent à la même portée. Une des trajectoires est appelée tir en cloche et correspond à l'angle initiale le plus grand, l'autre est appelé tir tendu et correspond à l'angle le plus faible.
En effet, l'équation $y_{\mathrm{max}} = \dfrac{v_0^2\,\sin 2 \alpha}{g}$ conduit à deux angles $\alpha$ du fait de la forme de la fonction sinus (on sait aussi que : $\sin\,u = c \Longleftrightarrow u = \arcsin c + 2k\pi \text{ ou } u = \pi - \arcsin c + 2k\pi$).

Flèche

Elle est définie par la hauteur maximale atteinte par le projectile. Pour trouver celle-ci, on utilise le fait qu'en ce point, la vitesse verticale du projectile est nulle :

On cherche le temps correspondant : $v_z(t_\mathrm{f}) = 0 \Longleftrightarrow t_\mathrm{f} = \dfrac{v_0\,\sin \alpha}{g}$

On remplace ce temps $t_\mathrm{f}$ dans l'expression de $z(t)$ :

Parabole de sûreté

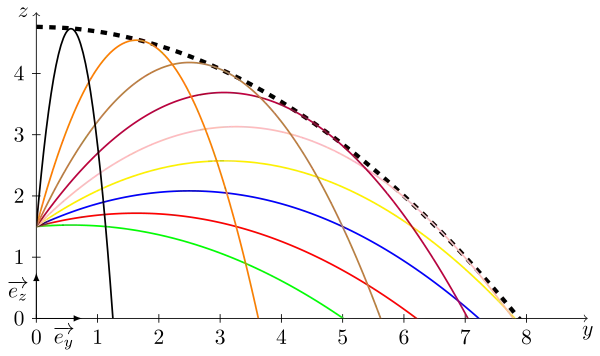
C'est une parabole qui délimite l'ensemble des points que l'on peut atteindre lorsque $v_0$ et $h$ sont fixés.

On peut montrer qu'elle passe par toute les flèches obtenues lorsque l'on fait varier l'angle de la vitesse initiale de 0 à 90°.

Elle est représentée en pointillés sur la figure ci-dessous :

Références

• "Physique Tout-en-un MPSI PCSI PTSI" - Marie-Noëlle Sanz / Anne-Emmanuelle Badel / François Clausset - Editions Dunod 2008 ;
• "Précis Mécanique PCSI" - C.Clerc / P.Clerc - Bréal ;