Collège/Lycée > Révisez votre cours

Questionnaire Première-Physique-chap 2 :
Caractéristiques du mouvement d'un solide

Rappels :

Complétez les phrases ci-dessous :

• Le mouvement d’un corps doît être décrit par rapport à un corps de ................... appelé ......................
  
  Le mouvement du corps ............... du choix de ce ......................
  
  Dans la plupart des cas, on se place dans un ....................... .................. comme le laboratoire par exemple. On peut alors étudier tous les mouvements classiques que l'on étudie en classe.
  
• En classe, tout corps étudié est assimilé à un solide que l'on définit comme tout corps qui ne subit pas de ......................... au cours du .................. étudié.
  
  
• Décrire le ...................... d'un corps, c’est connaître le ....................... de ................ de ses points.
  
  
• L’................. des positions prises par un point au cours du mouvement est appelé ..........................
  
  

Vitesse d'un point :

Vitesse moyenne :

• Définition :

  Donnez la formule permettant de calculer la vitesse moyenne d'un solide entre deux points (on note l la longueur du parcours, Δt le temps de parcours et V_moy la vitesse moyenne) :
  



• Application :

  Le record du monde du 100 m masculin détenue par Asafa Powell, est de 9,77 s.
  Calculez la vitesse moyenne en m.s^-1 puis en km.h^-1 du sprinter.
  

Vitesse instantanée :

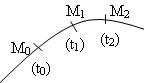
• Complétez :

  La vitesse ............................ V₁(t) d’un solide à la date t₁ est approximativement égale à la vitesse ..................., calculée entre deux instants ............... et ........................ la date t₁ :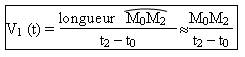
  
  
  

Vecteur vitesse :

Complétez :

• Pour représenter sur un schéma la ..................... du solide en un point de sa .........................., on utilise la notion de ................. ...................
  Comme son nom l'indique, il s'agit d'un .................. qui a donc .... caractéristiques :
  
  
  • Une ................... que l'on appelle aussi point ............................ : point pour lequel on a calculé la vitesse .............................
  • Une .................... : celle de la ......................; à la trajectoire au niveau du .......... .......................... considéré.
  • Un ........... : celui du ......................du solide, ce sens est représenté par la flèche du vecteur.
  • Une ............... qui correspond au calcul de la vitesse
    .......................... au point considéré.
  
  
• Plus la ................ ............................... du solide est grande,
  plus la .............. du vecteur vitesse sera grande,
  plus la .................. du vecteur sera grande.
  
  Pour lier ................... du vecteur et sa ................., on choisira une ..................., par exemple 1cm = 0.5 m/s.
  
• Sur le schéma ci-dessous dessinez le vecteur vitesse au point M₁ et nommez-le :
  
  
  

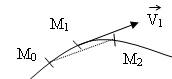
Un point particulier :

• Comment appelle-t-on le point d'un solide en mouvement qui a une trajectoire plus simple que celle des autres points ?
  


• Avec quel autre centre est-il confondu ?
  

Différents types de mouvement :

Noms des mouvements et évolution de la vitesse :

Complétez :

• Si la vitesse augmente lors d'un mouvement, on qualifie celui-ci d'....................
• Si la vitesse diminue lors d'un mouvement, on qualifie celui-ci de ..................... ou .................
• Si la vitesse reste constante lors d'un mouvement, on qualifie celui-ci d'......................

Mouvement de translation :

• Comment définit-on un mouvement de translation pour un solide (considérez un segment joignant deux points quelconques de ce solide) ?
  



• Complétez : dans un mouvement de translation :

  • Tous les points du solide ont une trajectoire ...........................
  • Tous les points ont à chaque instant le même ............... ....................(même direction, même sens et même valeur).
  
  
• Donnez trois types différents de translations,x:
  

Mouvement de rotation autour d'un axe fixe :

• Donnez quelques exemples de mouvements de rotation autour d'un axe fixe :
  



• Complétez les propriétés d'un tel mouvement :

  • Lorsqu'un solide est en rotation autour d'un axe fixe, les points de ce solide situés sur l'axe restent ..........................
  • Chaque point du solide décrit un ................. centré sur l'axe de ....................
  • L'angle θ décrit entre deux instants donnés est ................... pour tous les points du solide, c’est l’angle de rotation du solide.
    
    
  
  

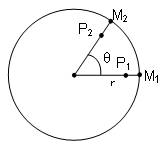
Vitesse angulaire :

• Complétez en vous aidant du schéma ci-dessus :

  
  Au cours d’'ne ...................., plus un point est .................... de l’axe, plus la longueur de l'arc décrit est ................. :
  arc(M1M2) > arc(P1P2) car M plus loin de l'axe que P.
  Ainsi les points du solide en rotation n'ont pas la même vitesse linéaire.
  
  En revanche, ils décrivent tous le même ..............., il est donc intéressant de caractériser ce mouvement avec la ..................... de variation de cet .............. appelée ............... .......................
  
• Donnez la formule permettant de calculer la vitesse angulaire d'un solide en rotation (on note θ l'angle de rotation, Δt la durée de rotation et ω_moy la vitesse angulaire (moyenne)) :
  

Relation entre vitesse linéaire et vitesse angulaire :

• En vous aidant de la formule de calcul du périmètre d'un cercle, trouvez une relation entre la longueur d'un arc de cercle et l'angle décrit par l'arc :
  


• Injectez l'expression de l trouvée précédemment dans la formule permettant de calculer la vitesse linéaire et déduisez-en la relation entre vitesse linéaire et vitesse angulaire :
  
  
  Remarque (rappel) :
  Pour passer d'un angle en degré à un angle en radian, il faut se rappeler que à 2π correspond 360°. On réalise la "conversion" en effectuant un produit en croix.