Licence 1 > Méthodes scientifiques > Cours 2 : pratiques de la démarche scientifique
MS2 : pratiques de la démarche scientifique
Introduction
Dans ce chapitre nous allons prendre un cas concret, le pendule simple, pour présenter quelques aspects importants de la démarche scientifique. Avant de modéliser puis de mettre en équation, nous allons nous intéresser à l’expérience et la notion de mesure : la physique est avant tout une science expérimentale !
Mesurer
Mesurer, c’est comparer
Grandeur physique, dimension, unité
Pour comparer, il faut s’intéresser à des choses de même nature. Comment sait-on que deux choses sont de même nature ? Tout d’abord, il faut définir la notion de grandeur physique : si on prend le cas du pendule simple que nous allons étudier par la suite, il possède quelques caractéristiques intrinsèques : sa période propre, sa fréquence d’oscillation, la longueur de son fil, ou bien encore la masse accrochée à l’extrémité du fil. Ces caractéristiques sont des grandeurs physiques.
Ainsi, pour mieux connaître notre objet pendule, on va chercher à connaître les valeurs de ces grandeurs : si on mesure la période du pendule, on va utiliser un chronomètre, le résultat de la mesure sera un temps qui pourra être exprimée avec différentes unités. Cet exemple nous permet d’introduire la notion de dimension et celle d’unité :
La grandeur physique période du pendule a la dimension d’un temps et peut s’exprimer en seconde (s), minute (mn) ou heure (h).
Donc finalement, lorsque l’on dit comparer des choses de même nature, cela signifie comparer des objets de même dimension.
Dimensions et unités de base du système international
La naissance du système international d’unité fait suite à différentes réflexions sur le système de mesure, notamment le système métrique, et ce depuis la révolution française.
A chaque une unité de base, correspond une définition : le mètre est défini à partir de la vitesse de la lumière, constante universelle ; la seconde à partir de transition énergétique dans l’atome de Césium, le kilogramme est la masse d’un prototype ... Ces définitions sont susceptibles d’évoluer, les scientifiques aimeraient reliés les sept unités de base à des constantes fondamentales.
Afin d’utiliser un système de référence commun, les physiciens ont établi une liste de sept dimensions qu’ils ont reliées à sept unités qui sont les unités de base du système international d’unité (SI). Ces dimensions sont indépendantes, toutes les autres grandeurs pourront s’exprimer dans une combinaison de ces dimensions.
| Grandeur/dimension | Unité SI |
|---|---|
| Longueur (L) | mètre (m) |
| Masse (M) | kilogramme (kg) |
| Temps (T) | seconde (s) |
| Intensité du courant (I) | ampère (A) |
| Température (\(\theta)\) | kelvin (K) |
| Quantité de matière (N) | mole (mol) |
| Intensité lumineuse (J) | candela (cd) |
Dimension d’une grandeur physique non basique
Le poids \(\overrightarrow{P}\) de la masse accrochée au bout du pendule simple est une force. Quelle est sa dimension ?
Pour trouver celle-ci, on utilise des relations qui nous permettent de lier la dimension de la grandeur recherchée avec les sept dimensions de base.Ici, la deuxième loi de Newton est \(\overrightarrow{F}=m\,\overrightarrow{a}\) donc \([F] \text{ (dimension de F)} = \mathrm{M.L.T^{-2}}\).
Ainsi, on pourra exprimer une force en \(\mathrm{kg.m.s^{-2}}\), en utilisant les unités de base. Mais on sait également que cette combinaison d’unité correspond au Newton (N), unité dérivée du système international qu’il est plus facile d’utiliser. Ainsi il existe de nombreuses unités dérivées des unités de bases : Hz, J, V, W, Pa, ...
On a réalisé ici une équation aux dimensions. Nous verrons son utilité par la suite.
Mesurer, c’est évaluer
Nous allons parler ici d’un aspect essentiel de notre science expérimentale : la mesure doit être soigneuse et accompagnée d’informations qui attestent de sa précision. Prenons ici l’exemple de la mesure de la période d’un pendule simple.
Notion d’erreur
L’erreur est la différence entre la valeur mesurée et la valeur vraie de la grandeur que l’on mesure. Il existe deux types d’erreurs :
L’erreur aléatoire que l’on traitera de façon statistique ou probabiliste : par exemple, la mesure répétée de la période d’un pendule avec un chronomètre manuel donne des valeurs légèrement différentes ;
L’erreur systématique est une erreur qui va se reproduire à chaque mesure (un biais) : par exemple, si la voie 1 d’un oscilloscope n’est pas mise à zéro initialement, la valeur d’une tension mesurée sur cette voie sera systématiquement entachée de la même erreur.
Quels types d’erreurs rencontrons nous pour la mesure de la période du pendule simple ?
erreur due au chronomètre : la précision du chronomètre n’est pas infinie, elle varie d’ailleurs avec le modèle de chronomètre utilisé. Lorsqu’on lit le résultat de la mesure, celui-ci est entaché d’une erreur aléatoire ;
erreur due au réflexe : là encore il s’agit d’une erreur aléatoire, le déclenchement et l’arrêt du chronomètre insère de l’erreur dans la mesure ;
erreur de positionnement (parallaxe) : si l’expérimentateur est mal positionné, il ne pourra pas déclencher et arrêter le chronomètre au bon moment. Il s’agit là d’une erreur systématique. On peut, autant que faire se peut, minimiser celle-ci en étant soigneux.
Notion d’incertitude
Évaluer l’incertitude équivaut à estimer l’erreur aléatoire commise lors d’une mesure. Elle donne accès à un intervalle autour de la valeur mesurée dans lequel est supposée appartenir la valeur vraie.
Deux types d’incertitudes
On distingue deux types d’incertitudes appelées "incertitudes-types" car exprimées à l’aide d’un écart-type :
- l’incertitude de type A est une incertitude évaluée statistiquement, sur un nombre donné de mesures : on répète un certain nombre de fois la mesure de la grandeur cherchée, on donne un résultat qui est la valeur moyenne des valeurs mesurées et une incertitude calculée statistiquement ;
- l’incertitude de type B est une incertitude évaluée sur une mesure.
Evaluation de l’incertitude de type B
L’erreur due au chronomètre est une incertitude de type B. On l’évalue avec une formule. Soit une indication est fournie par le constructeur, et on utilise celle-ci dans une formule de calcul :
\begin{equation}\boxed{u_B = \dfrac{\text{indication constructeur}}{\sqrt{3}}}\end{equation}
Soit on l’évalue directement avec une autre formule :
\begin{equation}\boxed{u_B = \dfrac{\text{une graduation ou une plage de valeurs acceptables}}{\sqrt{12}}}\end{equation}
Remarque
L’indication constructeur est aussi appelée tolérance. On peut encadrer la mesure de la manière suivante :
mesure - tolérance < mesure < mesure + tolérance
La plage de valeurs acceptables vaut donc \(2\times\text{tolérance}\). Soit :
\begin{equation}u_B = \dfrac{2\times\text{tolérance}}{\sqrt{12}} = \dfrac{2\times\text{tolérance}}{\sqrt{3\times 4}} = \dfrac{2\times\text{tolérance}}{2\sqrt{3}} = \dfrac{\text{tolérance}}{\sqrt{3}}\end{equation}
Les deux formules écrites précédemment sont en fait les mêmes.
Exemples
si on utilise le chronomètre au centième, l’incertitude est :
\begin{equation}u_B = \dfrac{0,01}{\sqrt{12}} = 3 \times 10^{-3}\,\mathrm{s}\end{equation}
si on utilise le chronomètre au millième, l’incertitude est :
\begin{equation}u_B = \dfrac{0,001}{\sqrt{12}} = 3 \times 10^{-4}\,\mathrm{s}\end{equation}
Nous mesurons ici une demi-période, donc l’incertitude sur la mesure de la période est deux fois plus importante, soit \(u_B(T) = 6 \times 10^{-4}\) (pour le chronomètre au millième).
- Si on mesure la longueur du fil du pendule, ce n’est pas seulement l’instrument qui cause de l’incertitude, mais notre manipulation : il est difficile de mesurer précisément cette longueur (repérage du centre d’inertie de la sphère métallique). Dans ce cas j’estime que la mesure se situe dans une plage à \(\pm 1\,\mathrm{mm}\) de la valeur lue. Cette plage vaut \(2\,\mathrm{mm}\), l’incertitude de type B vaut : \(u_B = \dfrac{0,002}{\sqrt{12}} = 6 \times 10^{-4}\,\mathrm{m}\).
Elargissement de l’incertitude
Peut-on faire confiance à l’incertitude-type de type B ? Est-on sûr que l’ensemble des valeurs mesurées sera dans l’intervalle défini par celle-ci ?
On attribue donc un niveau de confiance à cette incertitude. Sachant que l'incertitude $\sigma$ correspond à un intervalle de confiance de 68%, on créé une incertitude élargie. Pour un niveau de confiance de \(95\%\), on montre que l’incertitude élargie vaut deux fois l’incertitude-type de type B :
\begin{equation}\boxed{\Delta x = 2 \times \sigma_x}\end{equation}
Qu’obtient-on pour la mesure de la période du pendule simple avec un chronomètre au millième ? L’incertitude-type vaut \(u(T) = 6 \times 10^{-4}\) d’où une incertitude élargie de \(U(T) = 1 \times 10^{-3}\).
Evaluation de l’incertitude de type A
Cette incertitude est statistique, pour l’évaluer, on effectue un certain nombre de mesures (le plus possible) dont on déduit l’incertitude. Aussi, comme mesure, nous prendrons la valeur moyenne de toutes les mesures.
Mais nous ne ferons jamais dans nos cas un grand nombre de mesures. Ainsi, on utilise une méthode, appelée méthode de Student, qui coefficiente l’écart-type à la moyenne en fonction du nombre de mesures prises. Ces coefficients sont données, ils sont fonctions du niveau de confiance que l’on souhaite utiliser. Dans la table ci-dessous sont rassemblés les coefficients de Student pour un niveau de confiance à 95%.
| Nombres de mesures \(n\) | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Coefficient \(t\) | 12,7 | 4,30 | 3,18 | 2,78 | 2,57 | 2,45 | 2,37 | 2,31 | 2,26 |
Et le calcul de l’incertitude est donnée par :
\begin{equation}\boxed{u_A = t \times \dfrac{\sigma_{n-1}}{\sqrt{n}}} \qquad \text{où} \qquad \boxed{\sigma_{n-1} = \sqrt{\frac{\displaystyle\sum_{i=1}^n (x_i - \overline{x})^2}{n-1}}}\end{equation}
Faisons l’étude statistique avec le pendule simple sur 5 mesures :
| \(\dfrac{T}{2}\) | 0,700 | 0,695 | 0,697 | 0,695 | 0,695 |
On calcule la valeur moyenne des mesures : \(\overline{\dfrac{T}{2}} = 0,696\,\mathrm{s}\).
Puis \(\sigma_{n-1} = 2,2\,\times 10^{-3}\).
Et enfin \(u = 2,78 \times \dfrac{2,2 \times 10^{-3}}{\sqrt{5}} = 2,7 \times 10^{-3}\)
Attention, ici a été utilisée la demi-période propre ; l’incertitude sur la période est deux fois plus grande que l’incertitude sur la demi-période : \(u_T = 5 \times 10^{-3}\,\mathrm{s}\)
On rappelle ici que ce $\sigma$ est donné pour un niveau de confiance de 95% : il équivaut donc à une incertitude élargie de type B.
Remarque
Ici, l’incertitude de type A et celle de type B sont du même ordre de grandeur. Mais en règle générale, quelle étude vaut-il mieux mener ?
L'incertitude de type B se calcule en fonction de l'appareil de mesure ou d'une plage de valeurs acceptables évaluées par l'expérimentateur, alors que lors de l’étude statistique, on effectue un certain nombre de fois la mesure (et plus de fois on la fait, mieux c’est), elle permet de prendre en compte davantage de paramètres (comme le soin de l’expérimentateur.
L’incertitude statistique est donc plus judicieuse, seulement elle prend du temps ... si bien que l’on procède souvent à une évaluation de l’incertitude de type B.
Propagation des incertitudes
Lorsque une grandeur \(x\) dont on souhaite obtenir une mesure dépend d’au moins deux paramètres mesurables (\(p_1\), \(p_2\)); alors pour calculer l’incertitude sur la grandeur voulue, on doit tenir compte de l’incertitude de mesure sur chaque paramètre.
Souvent, on aura à faire à un produit, soit \(x = p_1^a \, p_2^b\). Alors le calcul d’incertitude sera le suivant :
\begin{equation}\boxed{\dfrac{u_x}{x} = \sqrt{\left(\dfrac{a\,u_{p_1}}{p_1}\right)^2+\left(\dfrac{b\,u_{p_2}}{p_2}\right)^2}}\end{equation}
Remarque
Avant de mener le calcul à son terme, on peut vérifier si un des termes n’est pas négligeable devant les autres ...
Exemple
On souhaite connaître la puissance électrique consommée par un conducteur ohmique \(P=R\,I^2\). On mesure sa résistance \(R = 15,7\,\Omega\) avec une incertitude-type \(u_R = 1\,\Omega\), puis on mesure l’intensité qui le traverse \(I = 0,274\,\mathrm{A}\) avec un incertitude \(u_I = 0,002\,\mathrm{A}\). On applique donc la formule proposée :
\begin{equation}\begin{aligned} \dfrac{u_P}{P} &= \sqrt{\left(\dfrac{1\,u_{R}}{R}\right)^2+\left(\dfrac{2\,u_{I}}{I}\right)^2} \\ & = \sqrt{\left(\dfrac{1}{15,7}\right)^2+\left(\dfrac{2\times 0,002}{0,274}\right)^2} \\ \Longleftrightarrow u_P &= \sqrt{\left(\dfrac{1}{15,7}\right)^2+\left(\dfrac{2\times 0,002}{0,274}\right)^2} \times 15,7 \times 0,274^2 \\ \Longleftrightarrow u_P &= 0,08 W \end{aligned}\end{equation}
Remarque
Le terme d’incertitude concernant l’intensité est bien inférieur à celui sur la résistance, nous aurions pu le négliger.
Ecriture du résultat d’un mesurage
On va juxtaposer le résultat de la mesure et l’incertitude élargie associée. On utilise la notation scientifique (puissance de dix), on écrira alors :
\begin{equation}\boxed{\text{valeur mesurée} = (x \pm \Delta x) \times 10^n \quad \text{unité}}\end{equation}
L’incertitude élargie sera donnée avec un seul chiffre significatif si le premier chiffre de l'incertitude est un 4 ou plus, on garde deux chiffres significatifs à l'incertitude si le premier chiffre de l'incertitude est un 1, un 2 ou un 3. Le nombre de chiffres significatifs de la valeur mesurée \(x\) sera cohérent avec l’incertitude (le ou les deux derniers chiffres significatifs de la valeur mesurée sont de mêmes "rangs" que le ou les deux chiffres significatifs de l’incertitude).
Exemple : période du pendule simple : \(T = 1,392 \pm 0,005\, \mathrm{s}\)
Modéliser
Modéliser, c’est analyser
Simplification du modèle
Le pendule simple est déjà la modélisation d’un phénomène physique réel, comme un enfant sur une balançoire.Mais pour que son étude théorique soit aisée, il faut simplifier au maximum le modèle. On prend donc la précaution :
d’utiliser une masse M lourde et suffisamment petite, pour que les frottements de l’air soit négligeables, pour que l’on puisse considérer être dans le cadre de la mécanique du point ;
d’utiliser un fil sans masse et inextensible, le frottement avec la potence doit être le plus faible possible ;
de lancer le pendule sans vitesse initiale et de le faire osciller avec de petits angles.
Comment justifier le fait qu’avec notre dispositif, les frottements de l’air sont négligeables ?
Nous savons que ce qui permet au pendule d’osciller c’est le poids de la masse suspendue à l’extrémité du fil. Nous pouvons alors calculer ce poids, calculer la force de frottements fluide, et comparer!
Le poids de la masse est donné par \(P = m\,g\). La masse de la bille métallique étant de \(29\,\mathrm{g}\), l’intensité de la pesanteur étant prise égale à \(9,81\,\mathrm{m.s^{-2}}\), on obtient :
\begin{equation}P = 0,029 \times 9,81 = 0,28\,\mathrm{N}\end{equation}
Intéressons-nous à la force de frottement fluide. Elle est a pour expression :
\begin{equation}F = \dfrac{1}{2}\,\mu\,S\,C_x\,v^2\end{equation}
Avec \(\mu\) la masse volumique du fluide, \(S\) la section de l’objet mobile dans le fluide, \(C_x\) le coefficient de trainée (de pénétration dans l’air) de l’objet mobile, \(v\) la vitesse de l’objet mobile. Comme nous souhaitons uniquement la comparer à \(P\), nous pouvons nous contenter d’obtenir un ordre de grandeur.
La masse volumique de l’air est d’environ \(1,2\,\mathrm{g.L^{-1}} = 1,2\,\mathrm{kg.m^3}\) (attention unité SI) ;
La section S vaut \(3 \times 10^{-4}\,\mathrm{m^2}\) ;
Le \(C_x\) d’une sphère dans l’air vaut \(0,4\) ;
On peut enfin estimer la vitesse (maximum) de notre bille : elle parcourt environ \(20\,\mathrm{cm}\) sur une demi-période, soit \(\dfrac{0,2}{0,7} = 8 \times 10^{-2}\,\mathrm{m.s^{-1}}\)
Ainsi : \(F = 1 \times 10^{_4} \times 0,4 \times (10^{-1})^2 \simeq 10^{-7}\,\mathrm{N}\)
\(F \simeq 10^{-7}\) contre \(P \simeq 10^{-1}\), aucun doute que dans ce cas les frottements sont négligeables.
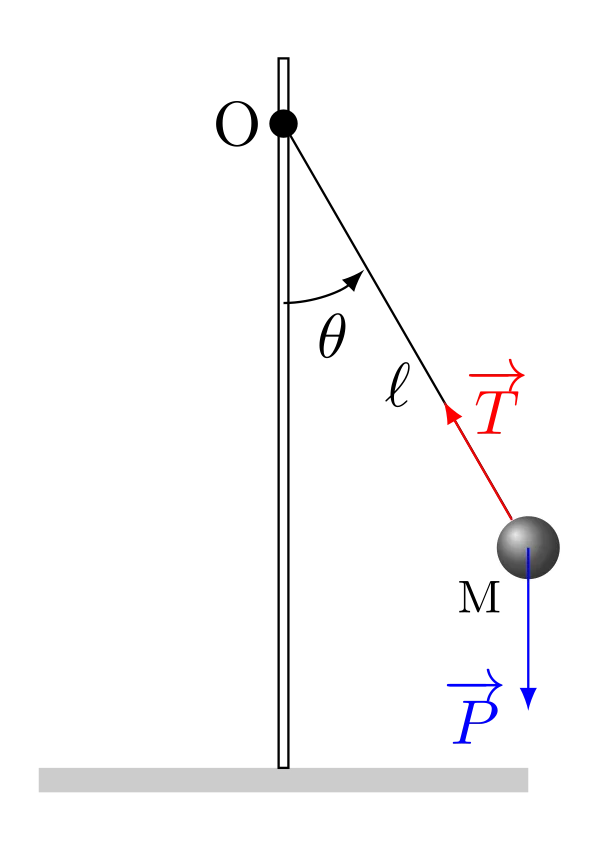
Schématisation du modèle
Pour raisonner, il est utile de bien représenter le modèle que l’on étudie. On procède à sa schématisation. On modélise aussi les actions mécaniques que subit la masse du pendule par des forces.
Modéliser, c’est mettre en équation
Débuter un problème de mécanique
Nous reverrons en détail ces quelques étapes dans le module de mécanique. Pour mettre en équation, il faut définir un référentiel, un système, faire le bilan des forces et utiliser une loi de la physique.
Donc ici :
Référentiel : du laboratoire, considéré comme galiléen ; base de projection (voir plus loin);
Système : la masse M du pendule simple;
Forces : elles ont été schématisées ci-dessus, il s’agit du poids de la masse M et de la tension du fil (frottements négligeables).
Loi de la physique : on utilise la deuxième loi de Newton, appelé principe fondamental de la dynamique : \(\sum \overrightarrow{F} = m\,\overrightarrow{a}\).
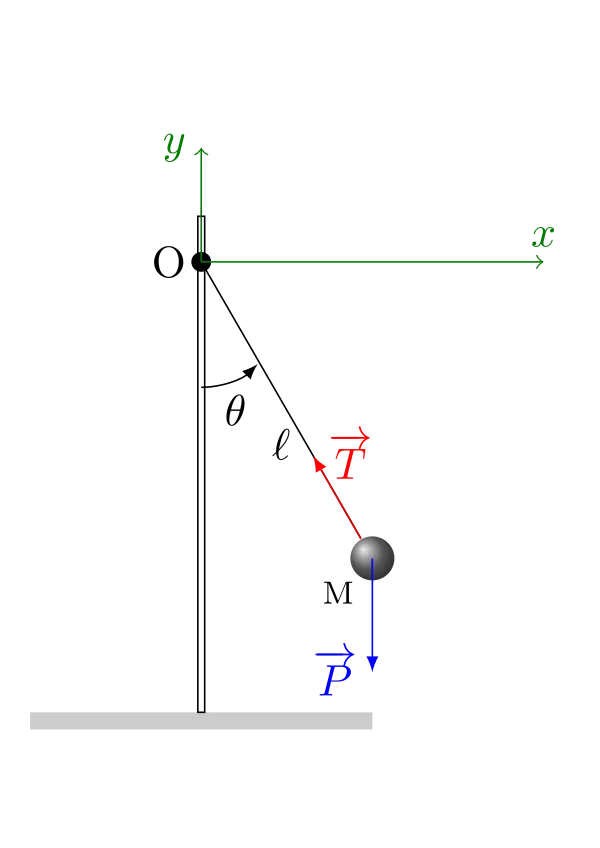
Grandeur pertinente et base de projection
Pour parvenir à décrire le mouvement de la masse M, il faut choisir la grandeur qu’il est pertinent de suivre. Ici, nous allons choisir la distance \(x\), l’abscisse, de la masse à la tige qui supporte le pendule.
Une base cartésienne sera utilisée pour cette étude (nous étudierons le pendule dans une autre base, plus classique, dans le module de mécanique). Dessinons-la :
Projection du PFD
On s’occupe alors de projeter le PFD sur la base choisie (quand on projette, il ne doit plus apparaître de vecteurs) :
\begin{equation}\begin{aligned} \sum \overrightarrow{F} = m\,\overrightarrow{a} &\Longleftrightarrow \overrightarrow{P} + \overrightarrow{T} = m\,\overrightarrow{a} \\ &\Longleftrightarrow \left\{\begin{array}{ccc} \text{Sur O$x$} :\quad 0 + - T\,\sin\,\theta &=& m\,\ddot{x}\\ \text{Sur O$y$} :\quad -P + T\,\cos\,\theta &=& m\,\ddot{y} \\ \end{array}\right. \end{aligned}\end{equation}
Approximations
Utilisons une simplification importante de notre modèle : dans l’hypothèse des oscillations de petits angles, on considère que le déplacement de la masse suivant l’axe O$y$ est négligeable : Si \(y \simeq 0\) alors \(\ddot{y} \simeq 0\).
Cela nous permet d’obtenir une expression de la force de tension dont on ne connaissait rien :
\begin{equation}T = \dfrac{P}{\cos\,\theta}\end{equation}
De plus, si \(\theta\) est petit, alors \(\cos\,\theta\) est très proche de 1. D’où finalement :
\begin{equation}T = P\end{equation}
Nous pouvons alors remplacer ce \(T\) dans l’expression du PFD projeté sur l’axe O$x$, ce qui donne :
\begin{equation}0 - P\,\sin\,\theta = m\,\ddot{x} \end{equation}
Obtention de l’équation différentielle
On doit maintenant chercher si la grandeur \(x\) ne s’est pas cachée dans les termes de l’équation : le sinus de l’angle \(\theta\) cache cette abscisse :
\begin{equation}\sin\,\theta = \dfrac{x}{\ell} \text{ donc } -\,m\,g\,\dfrac{x}{\ell} = m\,\ddot{x} \Longleftrightarrow \boxed{\ddot{x} + \dfrac{g}{\ell}\,x = 0}\end{equation}
Modéliser, c’est résoudre
Ne connaissant pas encore les solutions d’équations différentielles usuelles, cherchons graphiquement la solution de la fonction \(x(t)\).
Cherchons graphiquement la forme de la solution
La position initiale du pendule est l’endroit où \(x\) est le plus grand, celui-ci diminue, passe par zéro qui est son minimum puis ré-augmente en valeur absolue (\(x<0\)). Son maximum négatif est équivalent au maximum positif (pas de frottement) ...
A quelle fonction cela vous fait-il penser ?
Nous allons donc chercher une solution de l’équation différentielle sous la forme \(A\,\cos\,(a\,t)\) où \(A\) et \(a\) sont des constantes.
Comment déterminer les constantes ?
Détermination de \(a\)
Si l’expression de \(x\) écrite précédemment est la solution cherchée, \(x\) doit vérifier l’équation différentielle : pour montrer cela, on remplace \(x\) par \(A\,\cos\,(a\,t)\), et \(\ddot{x}\) par sa dérivée double. Calculons celle-ci :
\begin{equation}\begin{aligned} \dot{x} &= - a\,A\,\sin\,(a\,t) \\ \ddot{x} &= - a^2\,A\,\cos\,(a\,t)\end{aligned}\end{equation}
Puis remplaçons :
\begin{equation}- a^2\,A\,\cos\,(a\,t) + \dfrac{g}{\ell}\,A\,\cos\,(a\,t) = 0 \Longleftrightarrow \boxed{a = \sqrt{\dfrac{g}{\ell}}}\end{equation}
Ainsi, l’expression \(x = A\,\cos\,(a\,t)\) est solution de l’équation différentielle à condition que \(a = \sqrt{\dfrac{g}{\ell}}\).
Remarque
Par la suite, dés que vous verrez une équation différentielle, vous connaîtrez la forme de la solution Ainsi, vous déduirez \(a\) directement de l’équation différentielle.
Nature de \(a\)
Que représente a ? commençons par trouver sa dimension : le produit \(a\,t\) est l’argument d’une fonction trigonométrique, ce produit est donc sans dimension.Ceci signifie que \([a] = T^{-1}\).
Nous pouvons en déduire que \(a\) est une pulsation, la pulsation propre des oscillations notée généralement \(\omega_0\). Cette pulsation donne directement accès à la période \(T_0\) des oscillations, via la formule :
\begin{equation}\omega_0 = \sqrt{\dfrac{g}{\ell}} \Longleftrightarrow \boxed{T_0 = \dfrac{2\pi}{\omega} = 2\pi \sqrt{\dfrac{\ell}{g}}}\end{equation}
Remarque On parle de pulsation ou de période propres car il n’y a pas d’amortissement (frottements négligeables).
Détermination de \(A\)
Pour obtenir complètement la solution, nous devons trouver la valeur de la constante \(A\). Pour cela, on utilise les conditions initiales. Ici, nous avons une seule constante à trouver, il nous faut une seule condition. Nous avons lâché le pendule depuis son abscisse maximum \(X_m\), sans vitesse initiale : voilà les conditions initiales. Donc :
\begin{equation}\text{A } t=0 \text{, } A\,\cos\,(a \times 0) = X_m \Longleftrightarrow A = X_m\end{equation}
Remarque
Normalement pour équation du deuxième ordre, on a deux constantes à trouver donc il nous faut deux conditions initiales ... nous n’avons pas voulu compliquer les choses ici.
Finalement, l’évolution de l’abscisse du pendule s’écrit : \(\boxed{\mathrm{x(t) = X_m\,\cos\,\left(\sqrt{\dfrac{g}{\ell}}\,t\right)}}\)
Valider
Valider, c’est critiquer
L’expression de \(x(t)\) trouvée précédemment est-elle cohérente ? Intéressons nous surtout à l’expression de la période des oscillations : \(T_0 = 2\pi \sqrt{\dfrac{\ell}{g}}\) Cette expression est bien cohérente avec le fait que si la longueur \(\ell\) du pendule augmente, alors la période de celui-ci augmente. De la même manière, si l’intensité de la pesanteur diminue (imaginons l’expérience sur la lune), les oscillations seront plus lentes.
Utilisation d’une analyse dimensionnelle
Avant toute cette étude théorique, une équation aux dimensions nous aurait renseigner sur quelques aspects de l’expression de la période propre des oscillations et nous montrer que celle-ci ne dépendait pas de la masse. On liste tous les paramètres qui nous semblerait jouer un rôle sur la période propre des oscillations : la masse accrochée à l’extrémité, la longueur du pendule, l’intensité de la pesanteur, l’angle d’oscillations.
L’expression de la période pourrait être :
\begin{equation}T\,\propto\, m^{\alpha}\,\ell^{\beta}\,g^{\gamma}\,\theta^{\sigma}\end{equation}
avec \(\alpha,\beta,\gamma,\sigma\) des coefficients entiers ou rationnels. Passons aux dimensions :
\begin{equation}\begin{aligned} [T] &= M^{\alpha}\,L^{\beta}\,\left(\dfrac{L}{T^{2}}\right)^{\gamma} \\ \Longleftrightarrow T &= M^{\alpha}\,L^{\beta+\gamma}\,T^{-2\,\gamma} \end{aligned}\end{equation}
L’angle étant sans dimension, nous ne pouvons rien apprendre sur la dépendance de $T$ par rapport à l’angle d’oscillations.
Ainsi en identifiant les coefficients :
\begin{equation}\left\{\begin{array}{lll} \alpha = 0 \text{ la période propre des oscillations ne dépend pas de la masse}\\ \beta+\gamma = 0 \\ \gamma = -\frac{1}{2} = -\beta \end{array}\right.\end{equation}
Cette étude dimensionnelle nous permet d’écrire que l’expression de la période a pour forme :
\begin{equation}T = C^{\mathrm{ste}}\,\sqrt{\dfrac{\ell}{g}}\,f(\theta)\end{equation}
Ceci assure la cohérence avec l’expression trouvée à partir de l’étude théorique.
Valider, c’est confronter
À l’aide de nos mesures et de l’expression théorique de la période, nous pouvons confronter une valeur expérimentale de \(g\) avec la valeur tabulée : à Rennes, \(g = 9,81\,\mathrm{m.s^{-2}}\).
La période mesurée des oscillations est \(\overline{T} = 1,386\,\mathrm{s}\). Pour trouver la valeur de \(g\), nous avons besoin de la longueur du pendule. Nous mesurons celle-ci avec une règle graduée en mm : \(\ell = 48,0\,\mathrm{cm}\)
Extirpons \(g\) de l’expression de la période propre des oscillations :
\begin{equation}T_0 = 2\pi \sqrt{\dfrac{\ell}{g}} \Longleftrightarrow g = \dfrac{4\pi^2\,\ell}{T_0^2} = 9,86\,\mathrm{m.s^{-2}}\end{equation}
Il faut maintenant calculer l’incertitude sur la mesure de \(g\) par l’intermédiaire de deux mesures, celle de \(T\) et celle de \(\ell\). On utilise alors la propagation des incertitudes. Attention, celle-ci s’effectue avec des incertitudes-types, on élargie ensuite le résultat de la propagation.
Ici, l’incertitude-type sur la période a été évaluée à \(\sigma_{T_0} = 2 \times 10^{-3}\,\mathrm{s}\). Pour la mesure de \(\ell\), effectuée avec une règle graduée en millimètre, l’incertitude-type vaut : \(u_\ell = \dfrac{0,001}{\sqrt{12}} = 3 \times 10^{-4}\,\mathrm{m}\). Mais vu le protocole de mesure de cette longueur, on peut se permettre d’estimer une incertitude-type plus importante, disons un \(u_\ell\) de \(1 \times 10^{-3}\,\mathrm{m}\).
\begin{equation}\dfrac{u_g}{g} = \sqrt{\left(\dfrac{u_\ell}{\ell}\right)^2+\left(-2\dfrac{u_{T_0}}{T_0}\right)^2} \Longleftrightarrow U_g = 2 \times u_g = 7 \times 10^{-2}\,\mathrm{m.s^{-2}}\end{equation}
Conclusion
Notre mesure est la suivante :
\begin{equation}g = 9,86 \pm 0,07 \,\mathrm{m.s^{-2}} \Longleftrightarrow 9,79 < g < 9,93 \,\mathrm{m.s^{-2}}\end{equation}
La valeur tabulée appartient bien à cet intervalle, nous pouvons valider notre mesure de \(g\) avec ce matériel.
Remarque
Avec un \(u_\ell = \dfrac{0.001}{\sqrt{12}}= 3 \times 10^{-4}\), on obtient, après propagation, pratiquement la même incertitude-type sur \(g\).
Vérification d’une loi
Linéarisation
Une dernière chose importante que l’on peut aborder ici, c’est la vérification expérimentale d’une loi : La période des oscillations varie t-elle bien comme la racine carré de la longueur du pendule ?
Pour ne pas s’encombrer de la racine carré, on linéarise la loi : on cherche une fonction \(T^\alpha=f(\ell^{\beta})\) dont on pourra effectuer une régression linéaire.
\begin{equation}\text{Ici } T = 2\pi \sqrt{\dfrac{l}{g}} \Longleftrightarrow T^2 = \dfrac{4\pi^2}{g} \times \ell\end{equation}
Pour vérifier cette loi, il faut donc tracer la fonction \(T^2 = f(\ell)\). Le premier point de mesure est (\(\ell = 0,480 \pm 0.002\,\mathrm{m}, 1,386 \pm 0.004\,\mathrm{s})\). Nous pouvons effectuer deux ou trois mesures supplémentaires dans les mêmes conditions :(\(0,370\,\mathrm{m}, 1,222\,\mathrm{s}\)) ; (\(0,403\,\mathrm{m}, 1,280\,\mathrm{s}\)). On utilisera les mêmes incertitudes que précédemment.
Utilisation d’un tableur-grapheur
Utilisons un tableur-grapheur pour tracer la fonction désirée en faisant apparaître les ellipses d’incertitude : ces ellipses permettent d’avoir rapidement une idée sur ce que valent les incertitudes.
La modélisation nous permet de voir si la loi est validée (passage de la droite par les points de mesures aux incertitudes près) et d’obtenir une équation de la droite avec la valeur de sa pente et son incertitude. On peut en déduire une nouvelle fois la valeur de l’intensité de la pesanteur.
Traitement et résultats de notre expérience
Tableau de mesures
| i | \(\ell\) | \(u_\ell\) | T | \(u_T\) | \(T^2\) | \(u_T^2\) |
| 0 | 0,3700 | 0,001 | 1,222 | 0,002 | 1,493 | 0,009 |
| 1 | 0,4030 | 0,001 | 1,280 | 0,002 | 1,638 | 0,01 |
| 2 | 0,4800 | 0,001 | 1,386 | 0,002 | 1,921 | 0,01 |
Graphique et modélisation
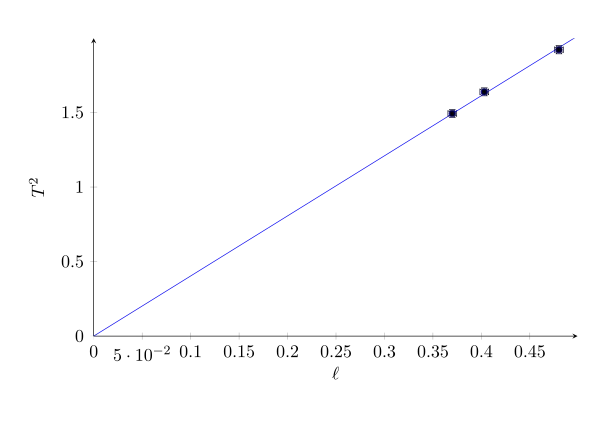
Résultat de la modélisation
Intervalle de confiance à 95%
Ecart expérience-modèle : 0,67 % sur \(T^2(\ell)\)
Chi2/(N-p)=1,04
a=(4,03 \(\pm\)0,08)
Obtention de $g$
On a : $a=\dfrac{4\,\pi^2}{g} \Longleftrightarrow g = \dfrac{4\,\pi^2}{a} = 9,796$.
On peut calculer l'incertitude sur cette mesure d'après la donnée de modélisation :
$\dfrac{U_a}{a} = \dfrac{U_g}{g} \Longleftrightarrow U_g = \dfrac{U_a}{a} \times g = 3 \times 10^{-2}$
cette mesure de $g$ grâce à la courbe $T^2=f(\ell)$ donne le résultat suivant : $ g = 9,80 \pm 0.03$.
Elle est compatible avec la valeur théorique ($9,81\,\mathrm{m.s^{-2}}$ à Rennes), ainsi qu'avec la mesure effectuée précédemment dans ce cours.
Vidéo sur la gestion des incertitudes avec le logiciel Regressi
La vidéo ci-dessous est chapitrée :
- Utilisation des incertitudes sous Regressi
- Utilisation des résultats donnés par Regressi
- Intérêt de la méthode du $\chi^2$
Exercice corrigé sur la linéarisation d'une loi : vérification de la loi de Stokes
Références
- L’astronomie dans l’apprentissage des mathématiques
- TangenteX : physique numérique
- Document de l’ENS de Montrouge sur les incertitudes
- Document de l’inspection pédagogique de physique chimie sur les incertitudes
- Un grand merci à Jimmy Roussel pour les idées et les titres des différents paragraphes de ce cours.