Licence 1 > Mécanique 1 > Cours 4 : Travail et énergies
M14 : Travail et énergies
Ce chapitre est disponible en vidéos. Vous trouverez la playlist dédiée ici :
Vous pouvez également visionner le chapitre séquence par séquence :
- Puissance et travail d'une force
- Energie cinétique et théorème de l'énergie cinétique (TEC)
- Forces conservatives et énergies potentielles
- Exemples de forces conservatives
- Energie mécanique, positions d'équilibre
Introduction
L’objectif de ce chapitre est de présenter les outils énergétiques utilisés en mécanique pour résoudre des problèmes. En effet, parfois le principe fondamental de la dynamique ne suffit pas ou n’est pas approprié pour parvenir au bout de la résolution.Avant de décrire les différents types d’énergies (énergies cinétique, potentielle et mécanique) et les utiliser dans des théorèmes énergétiques, nous présenterons les notions de puissance et de travail d’une force.
Travail et puissance d’une force
Puissance d’une force
Soit un point M qui se déplace sur sa trajectoire à une vitesse \(\overrightarrow{v}(M)\) par rapport au référentiel d’étude, Il subit une force \(\overrightarrow{F}\) telle qu’indiquée sur la figure ci-contre.
Alors la puissance de la force \(\overrightarrow{F}\) s’écrit :
\begin{equation}\boxed{\mathcal{P}(\overrightarrow{F}) = \overrightarrow{F} \cdot \overrightarrow{v}(M) = ||\overrightarrow{F}|| \times ||\overrightarrow{v}(M)|| \times \cos\,\theta}\end{equation}Cette force peut être qualifiée de trois sortes :
- elle est motrice, si sa puissance est positive ce qui correspond à un angle \(\theta < \frac{\pi}{2}\);
- elle est résistante, si sa puissance est négative ce qui correspond à un angle \(\theta > \frac{\pi}{2}\);
- enfin, elle peut être de puissance nulle, alors \(\theta = \frac{\pi}{2}\).
La vitesse du point M dépendant du référentiel d’étude, ce sera aussi le cas de la puissance de la force \(\overrightarrow{F}\).
Travail élémentaire d’une force
Servons-nous du déplacement élémentaire déjà défini au chapitre 1 : il s’agit du déplacement du point M sur sa trajectoire pendant un intervalle de temps infinitésimal \(\mathrm{d}t\).On calcule le travail élémentaire de la force \(\overrightarrow{F}\) de la manière suivante :
\begin{equation}\boxed{\delta W = \overrightarrow{F} \cdot \mathrm{d}\overrightarrow{OM}}\end{equation}Le vecteur \(\mathrm{d}\overrightarrow{OM}\) sera exprimé en fonction du système de coordonnées choisi.
Remarque
La notion \(\delta\) signifie que c’est le calcul d’un variation au cours d’un déplacement, en effet, la plupart du temps, le travail d’un force entre deux points dépend du chemin suivi entre ces deux points.Nous aurions noté un \(\mathrm{d}\) si il s’agissait d’une différence de grandeurs entre les deux points.
Exemple du vecteur déplacement élémentaire en coordonnées cartésiennes
Soit \(\overrightarrow{OM} = x\,\overrightarrow{u}_x + y\,\overrightarrow{u}_y + z\,\overrightarrow{u}_z\) que l’on différencie :
\begin{equation}\mathrm{d}\overrightarrow{OM} = \mathrm{d}x\,\overrightarrow{u}_x + \mathrm{d}y\,\overrightarrow{u}_y + \mathrm{d}z\,\overrightarrow{u}_z\end{equation}Travail d’une force
Généralement le travail d’une force dépend du chemin suivi, c’est pourquoi ce travail élémentaire est nécessaire. Pour obtenir le travail sur un déplacement AB, on intégrera ce travail élémentaire :
\begin{equation}W_{A\rightarrow B} = \int_{AB} \delta W = \int_{AB} \overrightarrow{F}\cdot \mathrm{d}\overrightarrow{OM}\end{equation}Cas des forces constantes
Lorsque la force est constante (vecteur constant en sens, direction et norme quel que soit le déplacement du point M), celle-ci peut sortir de l’intégration ci-dessus, on obtient :
\begin{equation}W_{A\rightarrow B} = \overrightarrow{F}\cdot \overrightarrow{AB} = ||\overrightarrow{F}||\times ||\overrightarrow{AB}|| \times \cos\,(\widehat{\overrightarrow{F}\,,\,\overrightarrow{AB}})\end{equation}On pourra parler de travail, moteur, résistant ou nul d’une force selon le signe de celui-ci.
Lien entre travail et puissance
A partir du lien entre le vecteur déplacement élémentaire et la vitesse, on peut lier puissance et travail :
\begin{equation}\mathcal{P} = \overrightarrow{F}\cdot \overrightarrow{v} = \overrightarrow{F}\cdot \dfrac{\mathrm{d}\overrightarrow{OM}}{\mathrm{d}t} = \dfrac{\overrightarrow{F}\cdot \mathrm{d}\overrightarrow{OM}}{\mathrm{d}t} = \dfrac{\delta W}{\mathrm{d}t} \quad \text{donc} \quad \boxed{\mathcal{P}=\dfrac{\delta W}{\mathrm{d}t}}\end{equation}Nous verrons par la suite (Paragraphe sur les forces conservatives et les énergies potentielles) des exemples de calcul de travaux de force.
Energie cinétique
Définition
L’énergie cinétique est l’énergie, en Joule, que possède un corps du fait de sa vitesse :
\begin{equation}E_\mathrm{C} = \frac{1}{2}\,m\,v^2\end{equation}Encore une fois, la vitesse de M dépendant du référentiel d’étude, son énergie cinétique en dépendra également.
Théorème de l’énergie cinétique
On se place ici en référentiel galiléen, ceci nous permet d’utiliser la seconde loi de Newton :
\begin{equation}\begin{aligned} \sum \overrightarrow{F}_\mathrm{ext} = m\,\overrightarrow{a} = m\,\dfrac{\mathrm{d}\overrightarrow{v}}{\mathrm{d}t} \\ \Longleftrightarrow \sum \overrightarrow{F}_\mathrm{ext} \cdot \mathrm{d}\overrightarrow{OM} = m\,\dfrac{\mathrm{d}\overrightarrow{v}}{\mathrm{d}t} \cdot \mathrm{d}\overrightarrow{OM} \\ \Longleftrightarrow \sum \delta W(\overrightarrow{F}_\mathrm{ext}) = m\,\dfrac{\mathrm{d}\overrightarrow{v}}{\mathrm{d}t} \cdot \overrightarrow{v}\,\mathrm{d}t \\ \Longleftrightarrow \sum \delta W(\overrightarrow{F}_\mathrm{ext}) = \mathrm{d}\left(\dfrac{1}{2}\,m\,v^2\right) = \mathrm{d}E_\mathrm{C} \end{aligned}\end{equation}On obtient alors la forme différentielle du théorème de l’énergie cinétique :
\begin{equation}\boxed{\delta W(\overrightarrow{F}_\mathrm{ext}) = \mathrm{d}E_\mathrm{C}}\end{equation}Ou bien en intégrant celle-ci entre deux positions (deux instants) A et B :
\begin{equation}\boxed{\sum W_{A\rightarrow B} (\overrightarrow{F}_\mathrm{ext}) = \Delta E_\mathrm{C} = \dfrac{1}{2}\,m\,v_B^2 - \dfrac{1}{2}\,m\,v_A^2 }\end{equation}Enfin, on peut exprimer ce théorème en considérant la puissance des forces :
\begin{equation}\sum \mathcal{P}(\overrightarrow{F}_\mathrm{ext}) = \dfrac{\mathrm{d}E_\mathrm{C}}{\mathrm{d}t}\end{equation}Exemple
Une descente en luge s’effectue sur une pente de longueur \(L=100\,\mathrm{m}\) entre A et B. La pente est caractérisée par un angle \(\alpha\). La vitesse initiale est nulle, que vaut la vitesse en B? On négligera tous les frottements.
On étudie le système luge dans le référentiel galiléen lié à la pente. La luge n’est soumis qu’à son poids. On applique le théorème de l’énergie cinétique (TEC):
\begin{equation}\begin{aligned} &W_{A\rightarrow B}(\overrightarrow{P}) = \dfrac{1}{2}\,m\,v_B^2 - \dfrac{1}{2}\,m\,v_A^2 \\ \Longleftrightarrow &\overrightarrow{P}\cdot \overrightarrow{AB} = \dfrac{1}{2}\,m\,v_B^2 \\ \Longleftrightarrow & m\,g\,L\,\sin\,\alpha = \dfrac{1}{2}\,m\,v_B^2 \\ \Longleftrightarrow & v_B = \sqrt{2\,g\,L\,\sin\,\alpha} = 31{,}3 \mathrm{m.s^{-1}} \end{aligned}\end{equation}Quand faut-il traiter un problème énergétiquement ?
La démonstration du TEC a pour origine le principe fondamental de la dynamique. On peut donc se demander quel est l’intérêt de celui-ci.La différence provient d’un traitement vectoriel ou non : avec le PFD, on doit le projeter sur la base choisie pour obtenir les équations, pas avec le TEC. Par contre quand le problème est à deux degré de liberté, on perd une information avec le TEC (puisque l’on obtiendra qu’une seule équation.
ConclusionL’utilisation du TEC est judicieuse lorsque le problème à résoudre est à un degré de liberté (on repère le système à l'aide d'une seule coordonnée). Il peut aussi s’avérer utile dans certain cas, pour un problème plus complexe.
Forces conservatives et énergies potentielles
Définition
Une force est conservative lorsque son travail entre deux points A et B ne dépend pas du chemin suivi mais uniquement de la position de ces deux points.
Elle dérive alors d’une énergie potentielle, grandeur qui caractérise énergétiquement le point M dans chaque position. On écrit :
\begin{equation}W_{A\rightarrow B} = E_\mathrm{P}(A) - E_\mathrm{P}(B) = - \Delta E_\mathrm{P}\end{equation}Ou de manière différentielle :
\begin{equation}\delta W = - \mathrm{d}E_\mathrm{P}\end{equation}Le signe est moins est présent par définition. Expliquons sa présence :
Interprétation
Les forces conservatives se nomment ainsi car elles laissent constante la somme de l’énergie cinétique et de l’énergie potentielle. En effet, appliquons le TEC dans le cas d’une force conservative :
\begin{equation}W(\overrightarrow{F}_\mathrm{cons}) = \Delta E_\mathrm{C} = -\Delta E_\mathrm{P} \Longrightarrow \Delta(E_\mathrm{C}+E_\mathrm{P}) = 0\end{equation}Une autre définition d’une force conservative
On rencontrera, pas seulement en mécanique, la définition d’une force conservative de la manière suivante :
\begin{equation}\boxed{\overrightarrow{F} = - \overrightarrow{\mathrm{grad}}\,E_\mathrm{P}} \end{equation}où le gradient est un opérateur mathématique qui dépend du système de coordonnées.
Si on travaille en coordonnées cartésiennes, \(f\) étant une fonction scalaire :\(\overrightarrow{\mathrm{grad}}f = \dfrac{\partial{f}}{\partial{x}}\overrightarrow{u}_x + \dfrac{\partial{f}}{\partial{y}}\overrightarrow{u}_y + \dfrac{\partial{f}}{\partial{z}}\overrightarrow{u}_z\).
Ecrivons de deux manière différente la différentielle de l’énergie potentielle :
- A partir de sa relation avec le travail élémentaire : \begin{equation}\mathrm{d}E_\mathrm{P} = -\delta W = - \overrightarrow{F}\cdot \mathrm{d}\overrightarrow{OM} = - \left|\begin{array}{l} F_x \\ F_y \\ F_z \end{array}\right. \cdot \left|\begin{array}{l} \mathrm{d}x \\ \mathrm{d}y \\ \mathrm{d}z \end{array}\right. = - F_x\,\mathrm{d}x - F_y\,\mathrm{d}y - F_z\,\mathrm{d}z \end{equation}
- A partir de la définition d’une différentielle : \begin{equation}\mathrm{d}E_\mathrm{P} = \dfrac{\partial{E_\mathrm{P}}}{\partial{x}}\mathrm{d}x + \dfrac{\partial{E_\mathrm{P}}}{\partial{y}}\mathrm{d}y + \dfrac{\partial{E_\mathrm{P}}}{\partial{z}}\mathrm{d}z \end{equation}
En identifiant les relations [vingtdeux] et [vingttrois] on a :
\begin{equation}\left|\begin{array}{l} F_x = - \dfrac{\partial E_\mathrm{P}}{\mathrm{d}x} \\ F_y = - \dfrac{\partial E_\mathrm{P}}{\mathrm{d}y} \\ F_z = - \dfrac{\partial E_\mathrm{P}}{\mathrm{d}z} \end{array}\right. \Longleftrightarrow \overrightarrow{F} = - \overrightarrow{\mathrm{grad}}\,E_\mathrm{P}\end{equation}Exemples de forces conservatives
Le poids
L’exemple le plus classique est le poids qui dérive de l’énergie potentielle de pesanteur. Calculons le travail élémentaire du poids :
\begin{equation}\delta W = -\mathrm{d}E_{\mathrm{PP}} = \overrightarrow{P}\cdot \mathrm{d}\overrightarrow{OM} = -m\,g\,\mathrm{d}z \quad \text{(travail en coordonnées cartésiennes)}\end{equation}En intégrant :
\begin{equation}E_{\mathrm{PP}} = m\,g\,z + \mathrm{cste}\end{equation}L’énergie potentielle est donc définie à une constante près, on devra fixer une origine. Ce sera le cas pour tout potentiel.
La force de rappel d’un ressort
Soit un ressort de constante de raideur \(k\) positionné le long d’un axe Ox horizontal. le support de celui-ci est à gauche, l’axe Ox dirigé vers la droite. L’allongement est \(x = \ell - \ell_0\). On a :
\begin{equation}\delta W = -\mathrm{d}E_{\mathrm{Pél}} = \overrightarrow{F}\cdot \mathrm{d}\overrightarrow{OM} = -k\,x\,\mathrm{d}x\end{equation}En intégrant :
\begin{equation}E_{Pél} = \dfrac{1}{2}\,k\,x^2 + \mathrm{cste}\end{equation}Exemple de force non conservative
Les forces de frottements ne sont pas conservatives. En effet, par exemple pour une force de frottement fluide :
\begin{equation}\delta W = \overrightarrow{f}\cdot \mathrm{d}\overrightarrow{OM} = -\alpha\,v_x\,\mathrm{d}x = -\alpha\,v_x^2\,\mathrm{d}t \quad \text{(exemple à une dimension)}\end{equation}On ne peut pas écrire cette relation sous forme de différentielle donc on ne peut pas définir une énergie potentielle.
En résumé
Une force est conservative si son travail sur un déplacement AB, ne dépend que de la position des points A et B, pas du chemin suivi entre A et B.
Toute force conservative n’est pas forcément constante (ex : force de rappel d’un ressort).Les forces de frottements sont non conservatives.
Energie mécanique
Définition
L’énergie mécanique d’un système est définie comme la somme de son énergie cinétique et de son énergie potentielle (qui peut avoir plusieurs sources):
\begin{equation}\boxed{ E_\mathrm{m} = E_\mathrm{C} + E_\mathrm{P} }\end{equation}Théorème de l’énergie mécanique
Non conservation de l’énergie mécanique
S’il y a variation de l’énergie mécanique, celle-ci est due aux forces non conservatives. On peut donc écrire :
\begin{equation}\boxed{ \dfrac{\mathrm{d}E_\mathrm{m}}{\mathrm{d}t} = \mathcal{P}_{\mathrm{non\,cons}} }\end{equation}On pourra appeler cette expression théorème de l’énergie mécanique.
Démonstration
Appliquons le théorème de l’énergie cinétique sous forme différentielle à un système soumis à des forces conservatives et non conservatives :
\begin{equation}\begin{aligned} \mathrm{d}E_\mathrm{C} &= \delta W_\mathrm{totale} \\ \Longleftrightarrow \mathrm{d}E_\mathrm{C} &= \delta W_\mathrm{cons} + \delta W_\mathrm{non\,cons} \\ \Longleftrightarrow \mathrm{d}E_\mathrm{C} & = - \mathrm{d}E_\mathrm{P} + \delta W_\mathrm{non\,cons} \\ \Longleftrightarrow \mathrm{d}(E_\mathrm{C}+E_\mathrm{P}) &= \delta W_\mathrm{non\,cons} \\ \Longleftrightarrow \mathrm{d}E_\mathrm{m} &= \delta W_\mathrm{non\,cons} \\ \Longleftrightarrow \dfrac{\mathrm{d}E_\mathrm{m}}{\mathrm{d}t} &= \dfrac{\delta W_\mathrm{non\,cons}}{\mathrm{d}t} = \mathcal{P}_\mathrm{non\,cons} \end{aligned}\end{equation}Conservation de l’énergie mécanique
Un système soumis à des forces conservatives ou qui ne travaillent pas possède une énergie mécanique constante.
\begin{equation}\dfrac{\mathrm{d}E_\mathrm{m}}{\mathrm{d}t} = 0 \end{equation}Cette équation [temcons] permet de retrouver facilement l’équation différentielle du mouvement d’un système classique. Par exemple pour le système solide-ressort :
\begin{equation}E_\mathrm{m} = \dfrac{1}{2}\,m\,v^2 + \dfrac{1}{2}\,k\,x^2 = \mathrm{cste} \Longrightarrow \dfrac{\mathrm{d}E_\mathrm{m}}{\mathrm{d}t} = m\,\dot x\,\ddot x + k\,x\,\dot x = 0 \Longrightarrow \ddot x + \dfrac{k}{m}\,x = 0\end{equation}Système conservatif, énergie mécanique et mouvements
Soit un système matériel conservatif, c’est à dire dont l’énergie mécanique est constante car il n’est soumis qu’à des forces conservatives.A partir de la définition de l’énergie mécanique, on peut écrire :
\begin{equation}E_\mathrm{C} = E_\mathrm{m} - E_\mathrm{P} \ge 0 \Longleftrightarrow E_\mathrm{m} \ge E_\mathrm{P}\end{equation}Comme l’énergie cinétique est une grandeur positive, l’énergie mécanique est forcément supérieure à l’énergie potentielle.
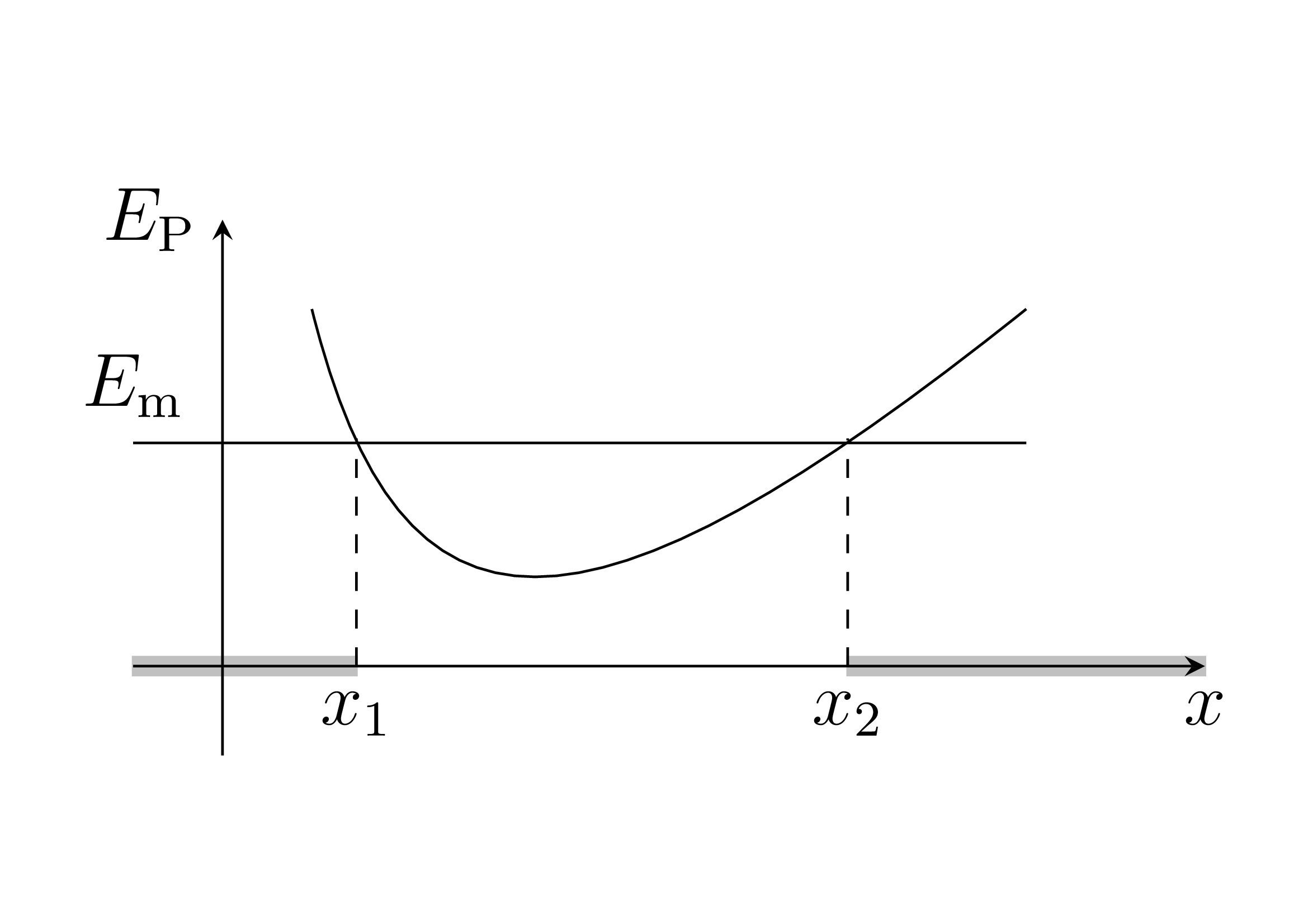
Ainsi à partir de l’allure de l’énergie potentielle (en fonction par exemple de la position), on peut connaître le type de mouvement : deux exemples classiques, la barrière de potentiel et le puits de potentiel :
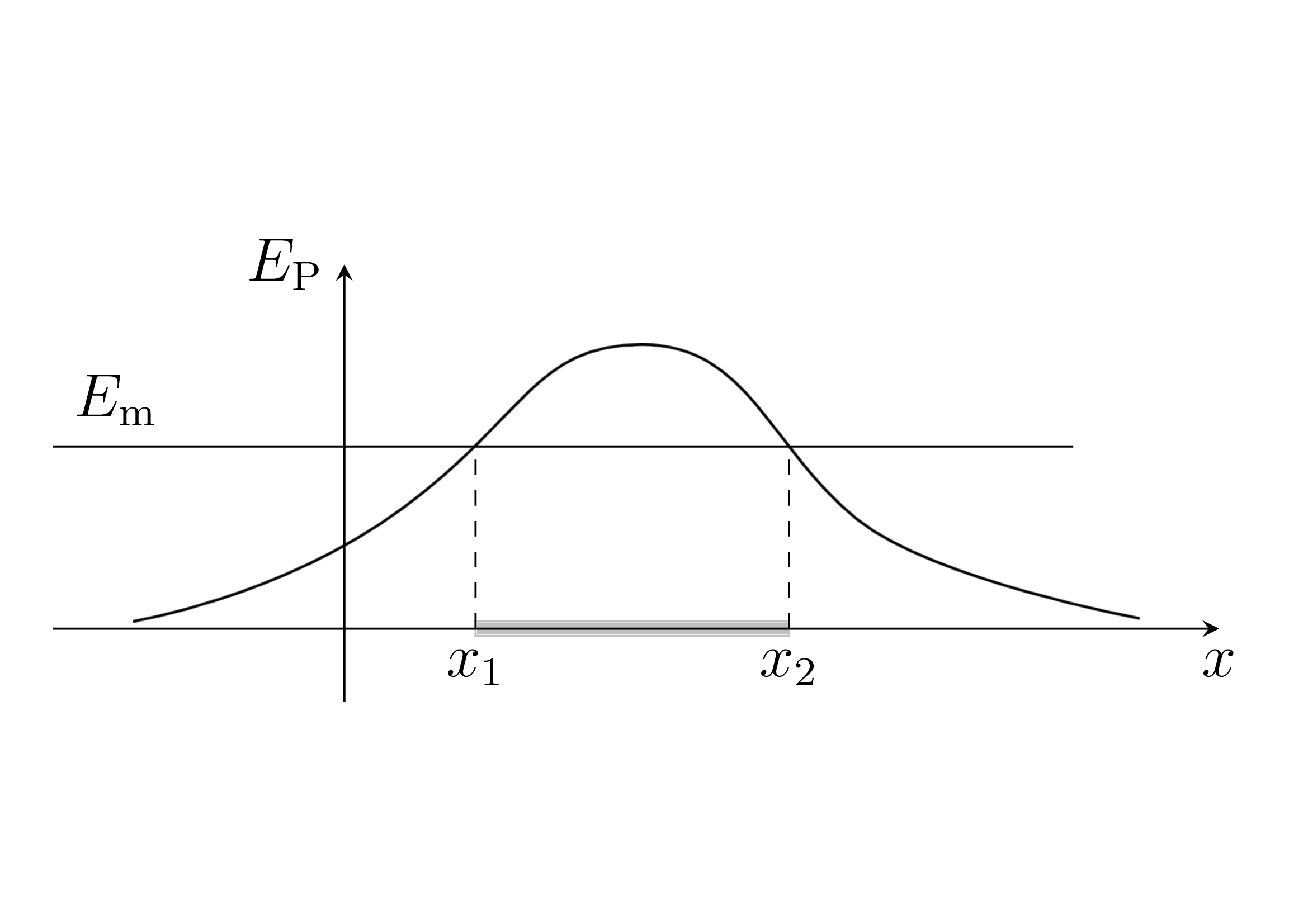
- Dans le premier cas, si le système est dans une position \(x \le x_1\), il ne peut jamais atteindre la position \(x_2\). De même s’il se situe dans une position \(x \ge x_2\), il ne peut pas atteindre la position \(x_1\).L’intervalle \(]x_1,x_2[\) constitue une barrière de potentiel, impossible pour le système de la franchir.D’autre part le système peut partir à l’infini, le mouvement n’est pas borné.
- Dans le deuxième schéma, c’est l’"inverse", le système est piégé dans l’intervalle \([x_1,x_2]\). Le mouvement est dans ce cas borné et périodique entre les positions \(x_1\) et \(x_2\).
Equilibres, énergie potentielle et stabilité
Notion d’équilibre
Un point matériel M de masse \(m\) est en équilibre lorsque toutes les forces qui s’exercent sur lui se compensent :
\begin{equation}\sum \overrightarrow{F}_{\mathrm{ext}} = \overrightarrow{0}\end{equation}En effet, la vitesse de M est nulle, son accélération est nulle donc d’après le PFD, la somme des forces est nulle.
Energie potentielle et positions d’équilibre
Soi un point matériel M soumis uniquement à des forces conservatives. On note \(\overrightarrow{F}\) la somme de ces forces et \(E_\mathrm{P}\) l’énergie potentielle globale dont dérivent ces forces conservatives. On suppose que cette énergie \(E_\mathrm{P}\) ne dépend que d’une seule variable (\(x\) par exemple).
On recherche les positions d’équilibres du point M, on a en ces positions :
\begin{equation}\overrightarrow{F} = - \overrightarrow{\mathrm{grad}}\,E_\mathrm{P} = \overrightarrow{0}\end{equation}Comme l’énergie potentielle ne dépend que de la coordonnées \(x\):
\begin{equation}\dfrac{\mathrm{d}E_\mathrm{P}}{\mathrm{d}x} = 0\end{equation}Les positions d’équilibre d’un système correspondent à un extrémum (minimum ou maximum) de l’ énergie potentielle.
Stabilité des équilibres
On peut montrer :
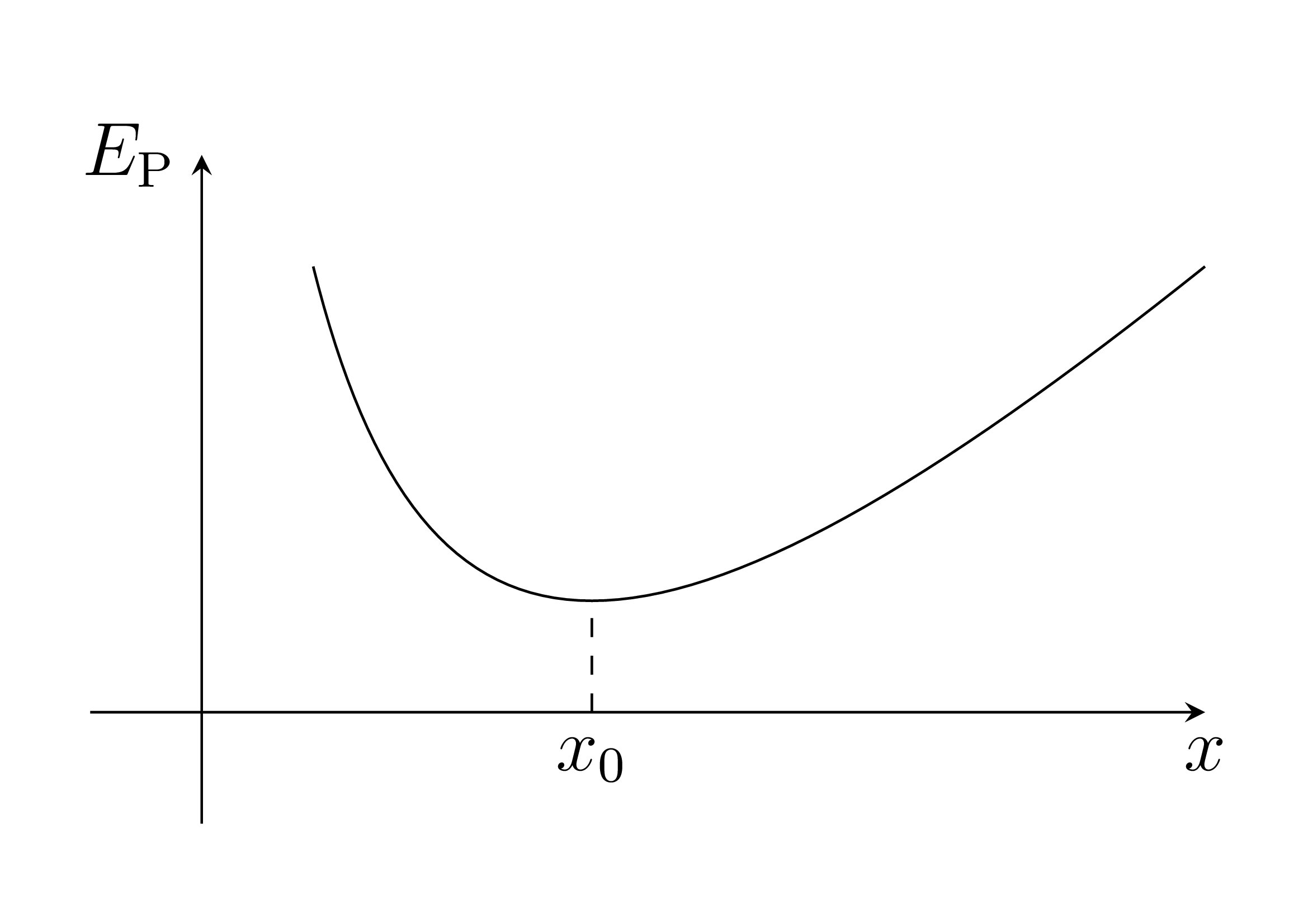
- qu’une position d’équilibre stable correspond à un minimum d’énergie potentielle. Alors : \(\dfrac{\mathrm{d}^2E_\mathrm{P}}{\mathrm{d}x} > 0\);
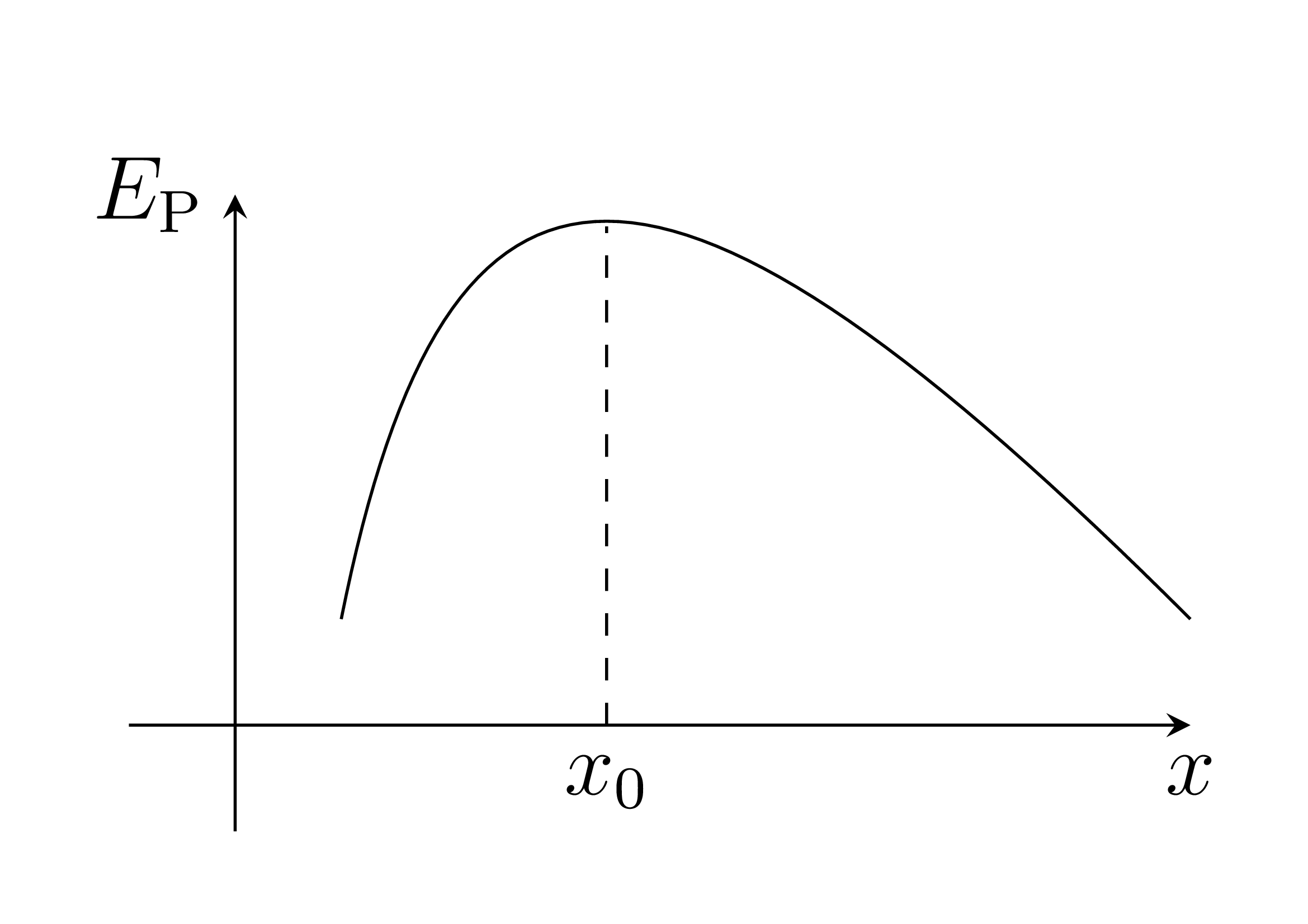
- qu’une position d’équilibre instable correspond à un maximum d’énergie potentielle. Alors : \(\dfrac{\mathrm{d}^2E_\mathrm{P}}{\mathrm{d}x} < 0\);
- "Physique Tout-en-un MPSI PCSI PTSI" - Marie-Noëlle Sanz / Anne-Emmanuelle Badel / François Clausset - Editions Dunod 2008 ;
- "Précis Mécanique PCSI" - C.Clerc / P.Clerc - Bréal ;
- Cours de physique par Damien Decout


