Licence 1 > Optique > Cours 4 : quelques instruments d'optique
O4 : instruments d'optique
Introduction
L’idée de ce cours est de présenter quelques instruments d’optiques classiques : on commencer par parler de l’œil puis de la loupe avant d’expliquer le principe d’instruments plus complexe comme la lunette astronomique. Enfin, nous aborderons quelques notions d’optique en relation avec l’appareil photographique (qu’il soit numérique ou argentique).
L'oeil
L’œil est l’organe de la vision qui peut être facilement modélisé au laboratoire par un ensemble diaphragme-lentille convergente-écran. Ainsi nos connaissances sur les lentilles minces nous permettent de comprendre le fonctionnement de l’œil, lorsqu’il est normal ou non.
L’organe et son modèle réduit
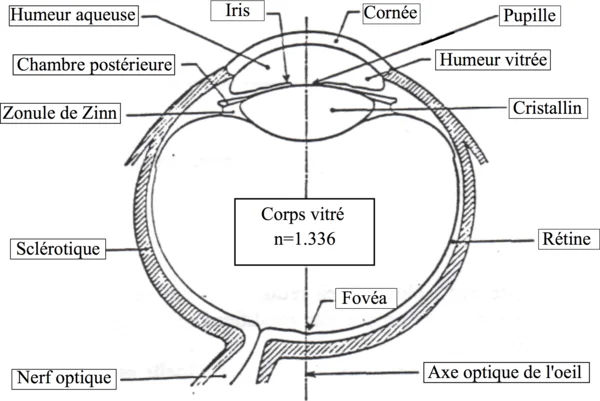
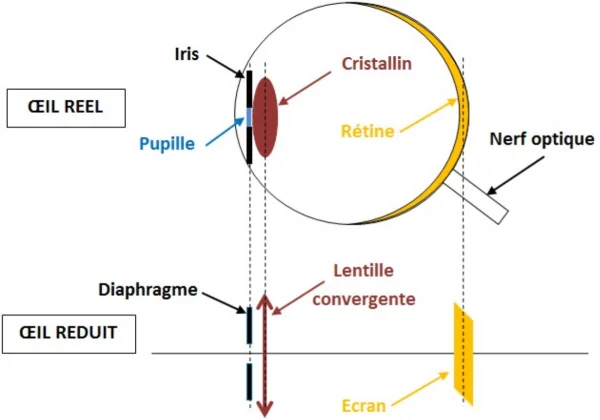
- L’œil est composé d’un ensemble de milieux transparents, mais on considère que le cristallin a le rôle le plus important en ce qui concerne la réfraction des rayons lumineux. Dans la modélisation optique, on assimilera donc la lentille au cristallin
- Pour moduler la quantité de lumière qui pénètre dans l’œil, l’ensemble pupille/iris joue le rôle de diaphragme.
- La rétine est l’écran de l’œil, elle est tapissée de deux types de cellules :
- Les cônes sont les cellules qui permettent la vision en couleur, de trois types différents, ils sont sensibles soit au rouge, soit au bleu soit au vert ;
- Les bâtonnets permettent la vision dans des conditions de faible luminosité.
- Via le nerf optique, les informations reçues par les cellules de la rétine arrivent au cerveau et sont interprétées en terme d’image.
Caractéristiques
Pouvoir de résolution
L’œil ne peut distinguer deux détails d’un objet que si leur image se forme sur deux cellules différentes de la rétine.Dans des conditions normales d’éclairement et de contraste, le pouvoir de résolution de l’œil est d’environ 1’ d’arc soit \(3\times 10^{-4}\,\mathrm{rad}\) (cela correspond à distinguer deux détails séparés de 1mm à une distance de \(3\,\mathrm{m}\)).
Vision à l’infini, vision de près
L’œil normal est appelé œil emmétrope. Nous étudions son cas ici.
- Pour obtenir une image nette, le cristallin fait converger les rayons lumineux reçus sur la rétine.
- Le point situé à la distance maximale qui permet la vision d’une image nette pour l’œil au repos est appelé Punctum Remotum (PR).Pour l’œil normal, celui-ci est à l’infini.
- Pour voir des objets plus près, l’œil doit accommoder, c’est à dire courber son cristallin pour que celui-ci devienne plus convergent.Il existe un point pour lequel l’œil est au maximum de sa convergence, qui correspond au point le plus proche dont on peut avoir une image nette : celui-ci est appelé Punctum Proximum (PP).Pour un œil normal, le P.P est à 25 cm de celui-ci.
Défauts de l’œil
- Si l’œil est trop convergent, il est myope : son PR n’est plus situé à l’infini mais à quelques mètres. L’oeil myope voit flou de loin, par contre ça vision de près est meilleure car le PP est plus proche. Pour corriger la myopie, on associe à l’œil une lentille divergente.
- Si l’œil est trop divergent, il est hypermétrope : cet œil est capable de voir à l’infini mais en accommodant. Le PP est plus éloigné de l’œil (il n’est pas assez convergent), la vision de près est moins aisée. Pour corriger ce défaut, on associe à l’œil une lentille convergente.
- La presbytie est un défaut qui vient avec l’âge de l’organe, le cristallin n’est plus assez souple pour se déformer à la demande. La vision de près qui demande au cristallin de devenir plus convergent est altérée.
- L’astigmatisme provient de la forme de l’œil qui n’est pas tout à fait sphérique, ce qui diminue la qualité de la vision que ce soit de près ou de loin.
La loupe
Le point le plus proche permettant une vision nette étant fixé (PP), pour mieux voir un objet, il faut utiliser un instrument : c’est ce que permet la loupe.
Pour obtenir l’effet Loupe, il faut que l’objet soit situé entre le centre optique d’une lentille convergente et son foyer objet : on obtient alors une image virtuelle, droite et agrandie.
De plus, afin que l’œil puisse observer cette image sans accommodation, celle-ci doit être à l’infini. La meilleure position de l’objet est celle où il sera sur le foyer principal objet.
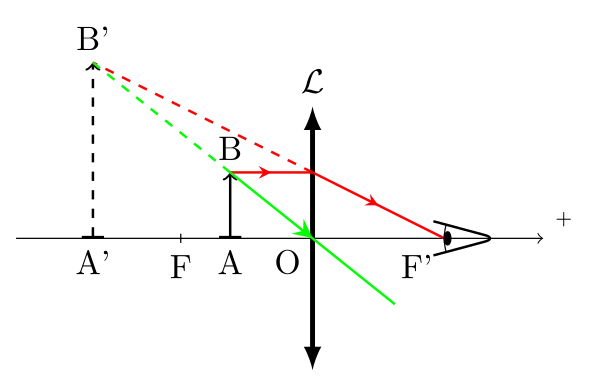
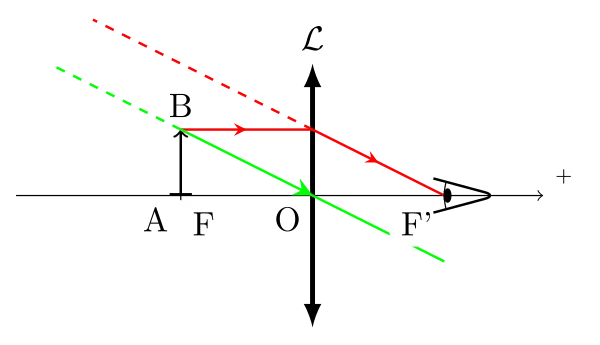
L’image obtenue avec une loupe peut-elle être plus ou moins grande? La distance objet-lentille joue-t-elle sur la taille de l’image observée?
La réponse est non :
- Si on approche l’objet de la lentille, l’image devient moins grande, mais elle est vue plus près ;
- Si on éloigne l’objet de la lentille (en gardant \(|\overline{OA}| < |\overline{OF}|\), l’image devient plus grande, mais elle est vue plus loin !
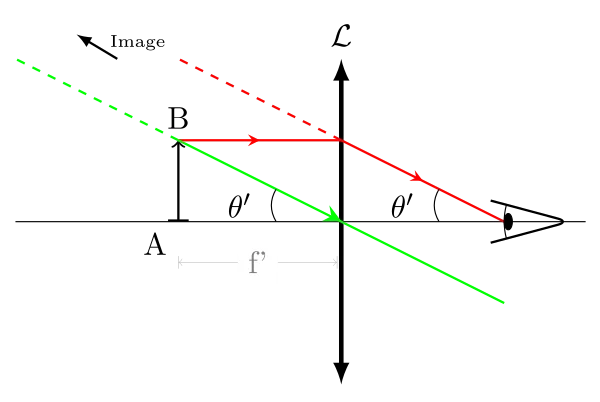
L’angle \(\theta'\) défini sur cette figure est le même quel que soit le cas, il ne dépend que de la lentille.
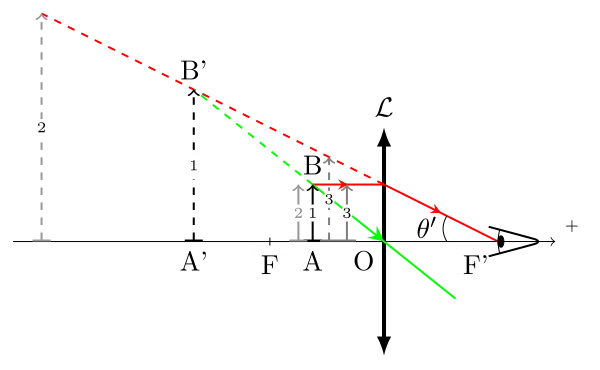
On définit alors le grossissement d’une loupe par le rapport entre :
- L’angle \(\theta'\) sous lequel est vu l’image ;
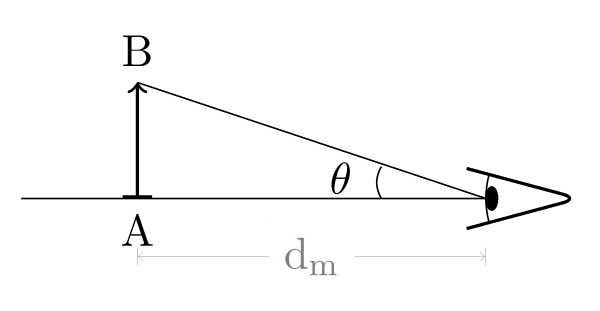
- L’angle \(\theta\) sous lequel est vu l’objet depuis l’œil à la distance de vision minimale de l’œil emmétrope soit \(\text{d}_m = 25\,\mathrm{cm}\).
On a donc :
\begin{equation}\boxed{G = \dfrac{\theta'}{\theta}}\end{equation}
Or si on note h la hauteur de l’objet, f’ la focale de la lentille convergente, on peut écrire dans le cas des petits angles :
\begin{equation}G = \dfrac{\theta'}{\theta} = \dfrac{\dfrac{h}{f'}}{\dfrac{h}{d_m}}= \dfrac{d_m}{f'}\end{equation}
Pour avoir un fort grossissement, il faut prendre une lentille de courte focale (de grande vergence).
L’appareil photo réflex
Description
On appelle appareil photo réflex, un appareil qui utilise un seul objectif pour la visée et pour la prise de vue.
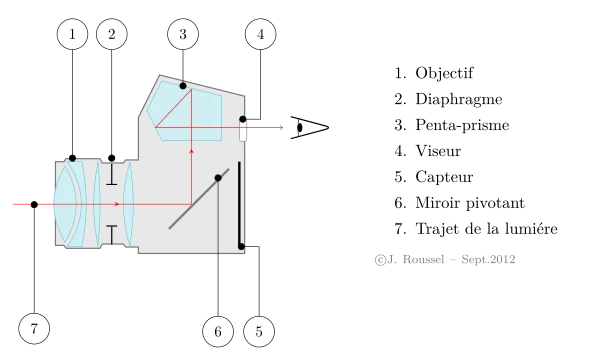
Pour se faire, l’appareil utilise un miroir plan incliné à \(45^{\circ}\) sur l’axe optique de l’objectif et un pentaprisme :
- Pour la visée, le miroir plan renvoie la lumière vers le pentaprisme qui la transmet à l’œil par l’intermédiaire du viseur ;
- Lorsque le photographe appuie sur le déclencheur, ce miroir plan pivote de façon à laisser passer la lumière vers le capteur.
Champ d’un appareil photo
Le champ d’un appareil photo est la portion d’espace qu’il peut photographier. Celui-ci dépend de la focale de l’objectif, mais aussi de la taille du capteur.
Influence de la focale de l’objectif
Voici des photos prises du même endroit avec un appareil muni d’un unique capteur mais avec des objectifs de focales différentes. A droite le schéma illustratif de la situation :


Donc plus la focale est grande, plus le champ est étroit, plus on capture un détail de l’image.
On dit que la première photo est prise avec un grand angle (focale courte, encombrement de l’appareil minimum), la deuxième est prise avec un téléobjectif (focale longue, encombrement important).
Influence de la taille du capteur
Voyons maintenant ce qu’il se passe si on garde une focale de 25 mm (première photo) mais que l’on diminue la taille du capteur. Sur des illustrations cela donne :
Ainsi, grand angle ne signifie pas forcément courte focale, car cela dépend de la taille du capteur.
Focale réelle et équivalente
Pour que tout le monde puisse identifier si un appareil sera un grand angle d’un téléobjectif, on a inventé la focale équivalente. C’est une focale calculée pour une seule taille de capteur (en l’occurrence un capteur \(24 \times 36\)).Si cette focale équivalente est grande, on a un téléobjectif, si elle est petite, on a un grand angle. C’est généralement cette focale équivalente qui est annoncée sur les appareils compacts à objectifs fixes.
Pour les objectifs des reflex qui sont généralement interchangeables, on indique sur ceux-ci leur focale réelle. On connaîtra donc le champ couvert par l’appareil que si on associe cette valeur réelle à la taille du capteur.Les fabricants d’appareils donnent alors le facteur de conversion permettant de passer de la focale réelle de objectif à la focale équivalente de l’ensemble objectif-capteur.
Voici alors l’utilisation des appareils selon leur focale équivalente :
- Jusqu’à 40 mm : grand angle ;
- 40-60 mm : standard ;
- 60-120 mm : focale à portrait ;
- 60-300 mm : téléobjectif.
La mise au point
Voici trois photos prises dans les mêmes conditions (même appareil, même focale, même endroit de prise de vue) mais avec trois mises au point différentes :



C’est elle qui détermine ce qui sera nette sur la photo finale et ce qui ne le sera pas. On la règle donc de façon à choisir le sujet à photographier. Elle peut se régler automatiquement (souvent en appuyant à mi-course sur le déclencheur), ou bien manuellement via une bague qui tourne autour de l’objectif.Sur cette bague, la mise au point est gradué en mètres : ”je veux faire la mise au point à 5 m de l’appareil”. Un objectif indique généralement les distances minimales et maximales de mise au point.
Prenons l’exemple d’une scène avec un homme situé devant un arbre :
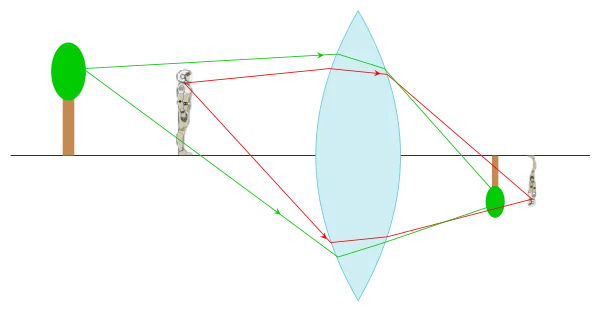
Je dois choisir qui je veux photographier. Si je choisis l’homme, je dois placer mon capteur au niveau de l’image de l’homme, les points objets de l’arbre donneront des taches images, ce qui donnera un arrière plan composé d’un arbre flou :
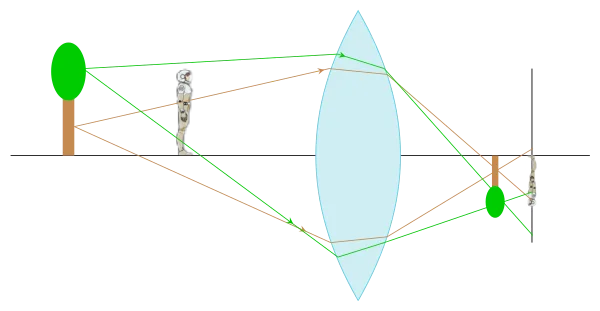
Donc la bague de mise au point doit agir sur la position du capteur par rapport à l’objectif pour sélectionner l’image à ”imprimer” ( dans le cas de l’homme, je fais la mise au point sur un objet proche, je dois éloigner mon capteur de l’objectif).Sur les appareils basiques, il y a vraiment déplacement, sur de plus perfectionnés, des lentilles de l’objectif se déplacent pour obtenir la mise au point voulue.
La profondeur de champ


Sur la première photo, nous voyons que le batracien est net, mais l’avant plan et l’arrière plan sont flous, la profondeur de champ est faibles.Sur la deuxième, les sabots comme la tête de l’animal sont nets alors qu’ils ne sont pas situés sur le même plan : la profondeur de champ est grande.
La profondeur de champ correspond à la zone de netteté en avant et en arrière du plan de mise au point : plus celle-ci est grande, plus la profondeur de champ est grande.
Profondeur de champ et ouverture
Celle-ci dépend de l’ouverture (diamètre d’entrée de l’objectif) que l’on règle à l’aide d’un diaphragme : plus l’ouverture est petite plus la profondeur de champ sera grande. Mais attention, la taille de l’ouverture influe sur la quantité de lumière qui imprégnera le capteur.
Cette ouverture est indiquée en fonction de la focale de l’objectif : une ouverture de \(\frac{f}{22}\) est plus petite qu’une ouverture de \(\frac{f}{4}\).
Voici deux schémas qui montrent pourquoi la réduction de l’ouverture agrandit la profondeur de champ :
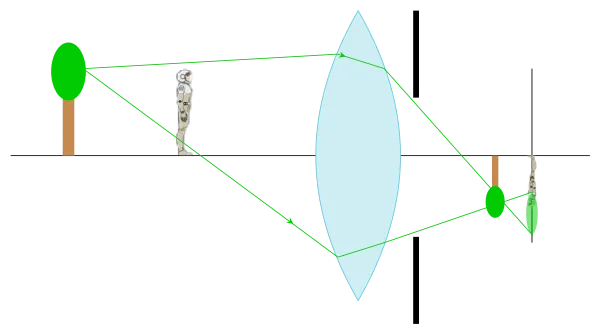
Avec un diaphragme ouvert, les feuilles des arbres créent une tache lumineuse assez large sur le capteur.
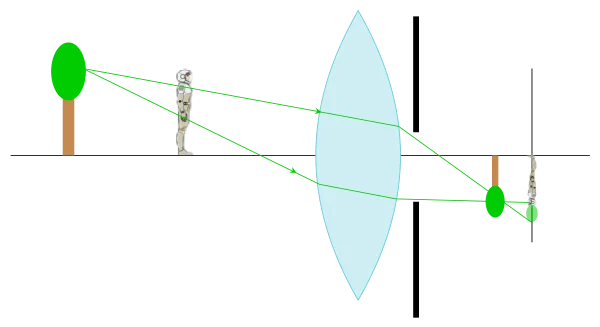
En réduisant l’ouverture, cette tache est plus petite. Si elle est inférieure à la taille d’un pixel du capteur (par exemple), les feuilles seront vues nettes.L’objet qui donnera une tache aussi grosse que les feuilles d’arbre du premier schéma sera plus loin en avant ou en arrière de l’homme, la zone de netteté sera plus importante.
Profondeur de champ et distance de mise au point
La profondeur de champ dépend aussi de la distance de mise au point : plus celle-ci est grande, plus la profondeur de champ est grande comme le montre le schéma suivant :
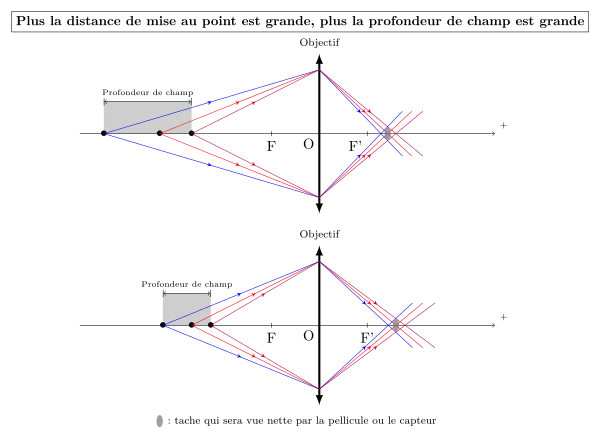
Profondeur de champ et focale
Enfin, la profondeur de champ dépend de la focale :
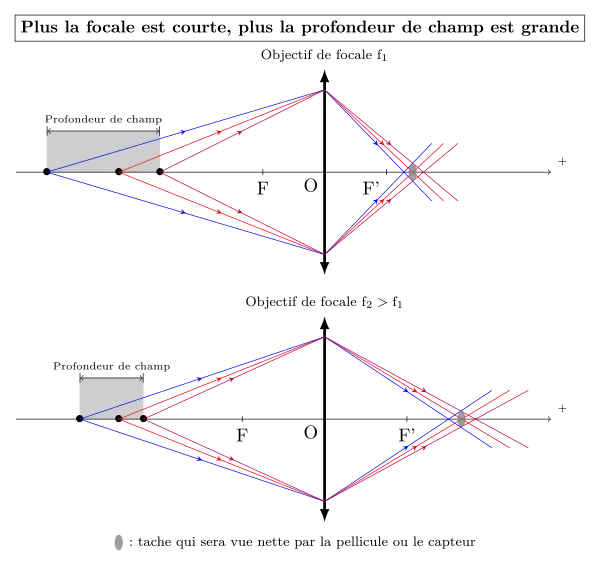
Attention aux réglages
Typiquement, on utilise une profondeur de champ faible, donc une grande ouverture pour effectuer des portraits, et une profondeur de champ importante lorsqu’il s’agit de photographier un paysage.Mais en même temps que l’on règle celle-ci, il faut penser à régler le temps d’exposition du capteur (le temps pendant lequel le miroir plan du reflex pivotera), car la photo risquerait d’être sur-exposée (pour un portrait) ou sous-exposée (pour un paysage).
Simulation des comportements d'un appareil
Vous pouvez vous rendre à l'adresse suivante pour tester les réglages principaux d'un appareil photo sur une prise de vue : https://camerasim.com/camerasim-free-web-app/
Présentation d'autres instruments optiques en vidéos
Lunette de Galilée
La lunette de Galilée est un instrument d'optique doté d'un objectif convergent et d'un oculaire divergent. L'intérêt de ce dernier est de permettre l'obtention d'une image droite, dans le même sens que l'objet. On peut alors réaliser grâce à cette lunette des observations terrestres.
La deuxième caractéristique de celle-ci est qu'elle est un système afocale, l'image d'un objet à l'infini se forme à l'infini, ainsi l'oeil de l'observateur n'aura pas besoin d'accommoder, il se fatiguera moins à l'observation. Pour réaliser une système afocal, on fait en sorte que l'image intermédiaire (image de l'objet par l'objectif) se forme sur le plan focale objet de l'oculaire.
Au niveau de la construction optique, on utilise toujours les rayons qui passent par le centre optique des lentilles qui ne sont pas déviés, afin de trouver la position de l'image intermédiaire et la direction dans laquelle observer l'image finale.
Enfin l'image intermédiaire permet également d'exprimer, par l'intermédiaire de l'angle sous lequel on voit l'image finale et l'angle sous lequel on voit l'objet, le grossissement de la lunette uniquement en fonction des focales des deux lentilles.
Lunette astronomique
Cette lunette est plutôt destinée à des observations astronomiques dans le sens où elle donnée d'un objet une image renversée par rapport à celui-ci.
Elle est composée d'un objectif et d'un oculaire convergent, c'est également un système afocal, le foyer image de l'objectif est confondu avec le foyer objet de l'oculaire de façon à ce que l'image de l'objet à l'infini soit à l'infini.
On utilise les rayons qui passent par le centre optique des lentilles pour effectuer la construction : obtention de l'image intermédiaire et de la direction de l'image finale.
L'image intermédiaire permet, comme pour la lunette de Galilée, de relier angle sous lequel on voit l'objet et angle sous lequel on voit l'image pour permettre l'expression du grossissement en fonction des focales de l'objectif et de l'oculaire.
Microscope
Le microscope, composé d'un objectif et d'un oculaire convergents, n'est pas un système afocal. On observe un objet très proche du foyer objet de l'objectif et on en fait une image (intermédiaire) via l'objectif, que l'on place sur le foyer objet de l'oculaire.
Ainsi une nouvelle fois, l'image finale sera à l'infini, pour éviter à l'oeil de l'observateur d'accommoder.
La particularité du microscope tient dans le fait que les deux lentilles, objectif et oculaire, sont solidaires d'un même tube. La mise au point du microscope (le fait de faire coïncider l'image intermédiaire avec le foyer objet de l'oculaire) est réalisée grâce au déplacement du tube par rapport à l'objet.
Le grossissement du microscope dépend de l'angle sous lequel on voit l'image de l'objet à travers l'instrument et de l'angle sous lequel on voit l'objet à la distance minimum de vision distincte de l'oeil emmétrope.
On montre que ce grossissement peut s'exprimer uniquement en fonction des focales de l'objectif et de l'oculaire, ainsi que de l'intervalle optique, distance entre le foyer image de l'objectif et le foyer objet de l'oculaire, et de la distance minimum de vision distincte.


