Licence 1 > Electrocinétique > Cours 2 : condensateur et bobine
EC2 : condensateur et bobine
Une grosse partie de ce chapitre est disponible en vidéos, la première de la playlist est ici :
Voici le lien vers les 4 films qui la composent :
- Introduction
- Charge du condensateur
- Décharge du condensateur
- Etablissement et rupture du courant dans un circuit RL
Introduction
Nous avions donné dans le chapitre EC1 une définition réductrice de ce qu’est un dipôle linéaire (sa caractéristique est une droite).
En réalité, tout dipôle pour lequel \(u\) et \(i\) sont reliés par une équation différentielle linéaire à coefficients constants est un dipôle linéaire.
Le cas le plus simple correspond au conducteur ohmique où \(u = R\,i\). Nous allons voir ici le cas du condensateur et de la bobine qui sont donc aussi des dipôles linéaires.
Circuits linéaires du premier ordre soumis à un échelon de tension
Différents types de régimes
En électricité, on emploie souvent le terme de régime de fonctionnement : nous allons en rencontrer de différentes sortes et il ne faut pas les confondre.
Le régime continu et le régime variable sont à opposer :
En régime continu, toutes les grandeurs électriques sont constantes au cours du temps ;
En régime variable, ces grandeurs dépendent du temps.
Le régime transitoire et le régime permanent vont de pair :
Un régime est permanent lorsque pendant un certain temps, les caractéristiques des grandeurs électriques ne sont pas modifiées.
Le régime continu est un cas particulier de régime permanent.
Un régime variable peut être permanent : nous verrons le régime sinusoïdal qui est variable (l’intensité et la tension sont des fonctions trigonométriques périodiques), mais comme les caractéristiques de \(i(t)\) et \(u(t)\) restent les mêmes, ce régime est aussi permanent.Un régime transitoire est le régime durant lequel on passe d’un régime permanent à un autre.
Échelon de tension
Nous allons soumettre différents circuits à un échelon de tension : on fait passer la tension aux bornes du circuit à étudier d’une valeur \(E_1\) à une valeur \(E_2\) en un temps très court considéré comme nul.
Pour cela, deux possibilités :
On ferme ou on ouvre un interrupteur qui relie un générateur de tension continue a u circuit à étudier.
On utilise un générateur basse fréquence (GBF) qui peut délivrer une tension créneau de fréquence variable.
Dans ce cas, il faut régler la fréquence du GBF en fonction de ce que l’on souhaite observé (généralement on la règle par rapport à la durée du régime transitoire à observer).

Circuit RC
Dans la vidéo ci-dessous, après une présentation du condensateur, on cherche l'équation différentielle régissant la charge d'un condensateur à travers un conducteur ohmique puis on la résout. On trace alors l'allure de la solution, et on détermine la constante de temps $\tau$.
Équation différentielle
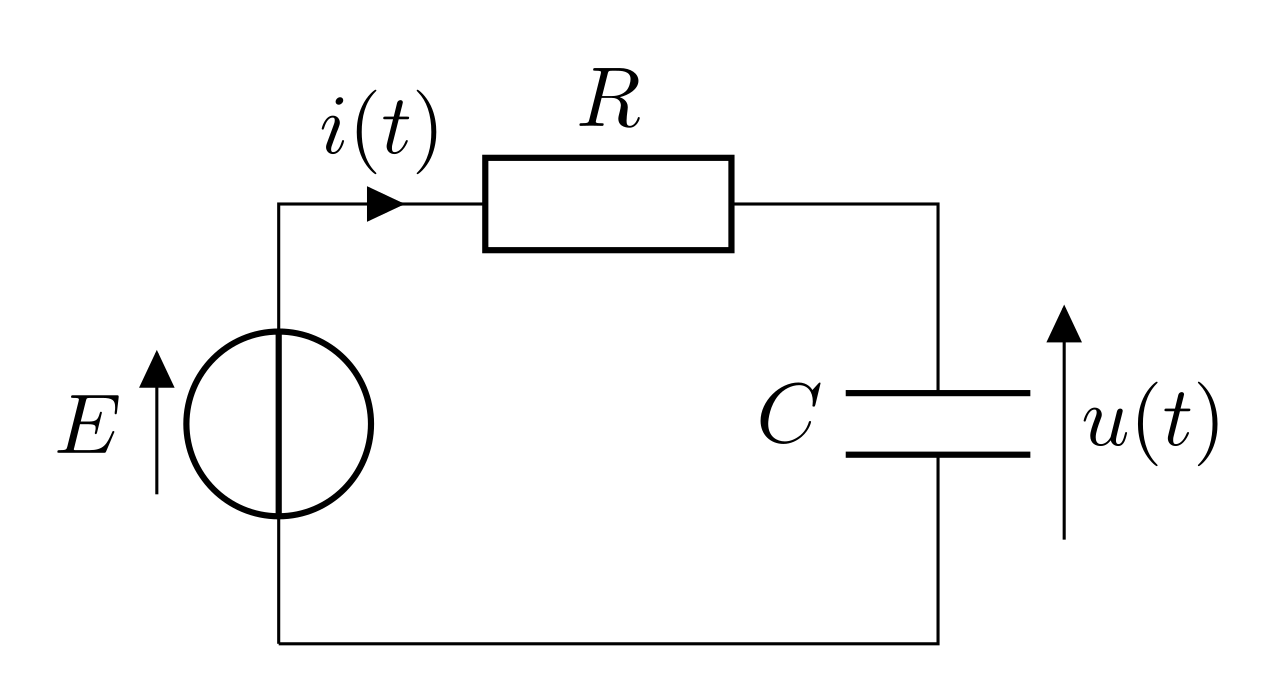
On étudie le circuit RC soumis à une tension \(E=\mathrm{cste}\), on s’intéresse à l’allure de la tension aux bornes du condensateur et à l’intensité parcourant le circuit.
Initialement, le condensateur est déchargé.On applique la loi des mailles :
\begin{equation}E = Ri + u\end{equation}
Or \( i=C\dfrac{\mathrm{d}u}{\mathrm{d}t}\), d’où
\begin{equation}E = RC\dfrac{\mathrm{d}u}{\mathrm{d}t} + u\end{equation}
Équation que l’on peut écrire :
\begin{equation}\boxed{\tau\dfrac{\mathrm{d}u}{\mathrm{d}t}+u = E} \end{equation}
avec \(\tau = RC\).
Cette équation différentielle est du premier ordre, le circuit RC est appelé circuit du premier ordre.
Cas de notre étude
La solution de cette équation différentielle sera différente selon le cas étudié.
Pour obtenir la solution la plus générale, on additionne :
une solution de l’équation homogène associée (sans second membre) qui correspond à la réponse du circuit RC sans excitation : c’est ce que l’on appelle le régime libre ;
une solution particulière qui correspond au régime permanent.
On s’intéressera ici au circuit soumis à un échelon de tension : le générateur délivre \(E\) pour la charge du condensateur, \(0\) pour sa décharge dans la résistance.
Charge du condensateur
On doit trouver une solution à l’équation : \(\tau \dfrac{\mathrm{d}u}{\mathrm{d}t} + u =E\).
Solution de l’équation homogène
On cherche une solution à l’équation homogène de la forme \(u_1 = A e^{\alpha\,t}\) avec A une constante et \(\alpha\) un réel.
Injectons \(u_1\) dans l’équation homogène :
\begin{equation}\tau \times \alpha A e^{\alpha\,t} + A e^{\alpha\,t} = 0\end{equation}
Ce qui donne \(\alpha = -\dfrac{1}{\tau}\)
Solution particulière
On cherche une solution particulière \(u_2\) constante.
On a \(\dfrac{\mathrm{d}u_2}{\mathrm{d}t} = 0\) donc \(u_2 = E\).
Solution globale
elle s’écrit : \(u(t) = A e^{-\frac{t}{\tau}} + E\).
Utilisation de la condition initiale
L’équation différentielle que nous étudions est du premier ordre, une seule condition initiale suffit à trouver la seule constante à déterminer :
A \(t=0\), \(u(t)=0\) donc \(A+E = 0\) et \(A = -E\).
Finalement, la tension aux bornes du condensateur qui se charge s’écrit :
\begin{equation}\boxed{u(t) = E \left(1 - e^{-\frac{t}{\tau}}\right)}\end{equation}
Et son allure est représentée ci-contre. On peut vérifier que la fonction \(u(t)\) est bien continue.
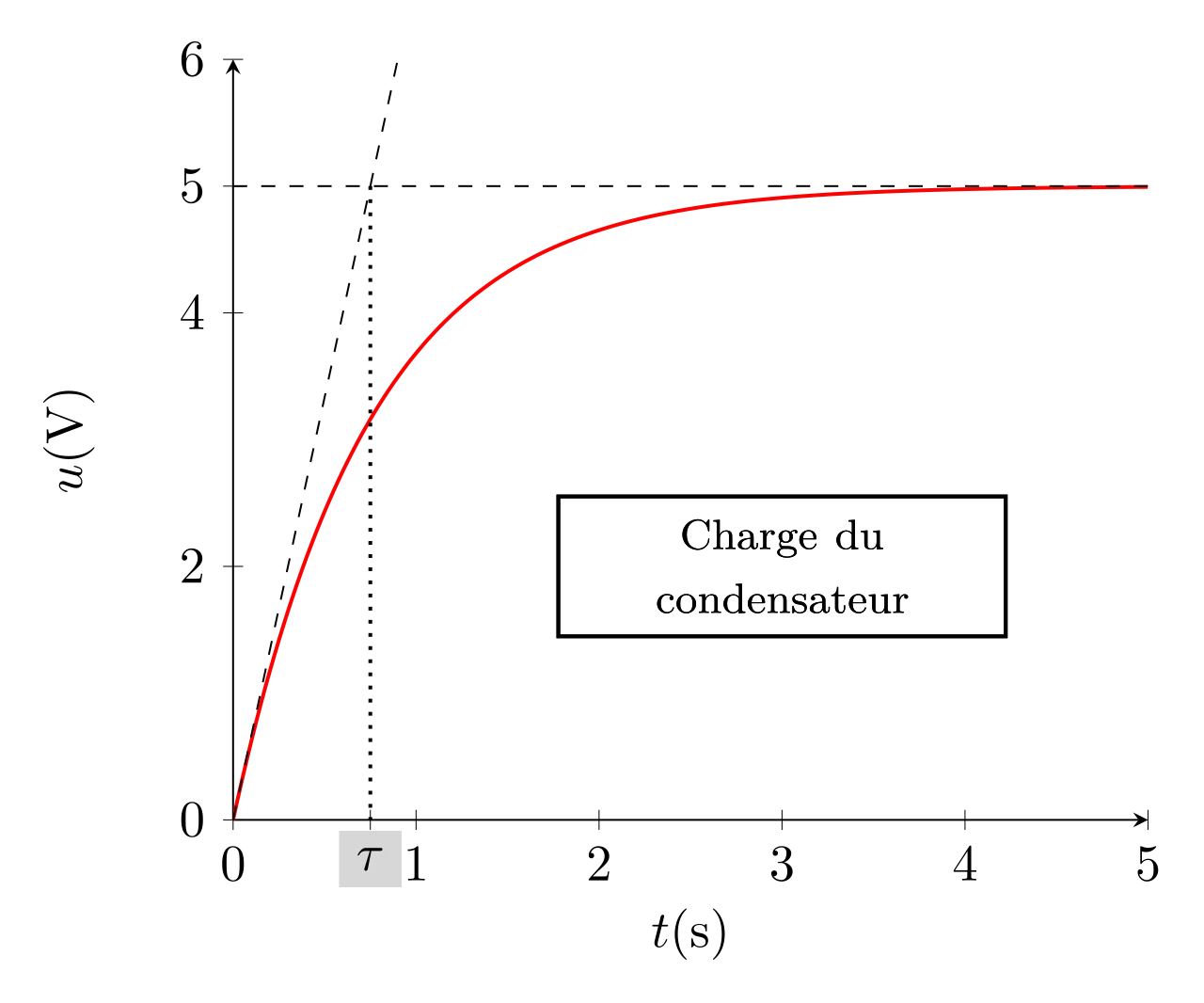
Comme le montre la figure ci-dessus, la constante de temps \(\tau = RC\) peut être facilement obtenue graphiquement. Ce temps permet de caractériser la vitesse de charge du condensateur, plus il est faible plus le condensateur se charge vite.
On dit aussi souvent qu’au bout d’un temps t égal à \(5\tau\), le condensateur est totalement chargé. On est passé du régime transitoire au régime permanent.
Intensité dans le circuit
On peut facilement obtenir l’équation de l’intensité du courant et son allure.
En effet, \(i =C\dfrac{\mathrm{d}u}{\mathrm{d}t}\) d’où :
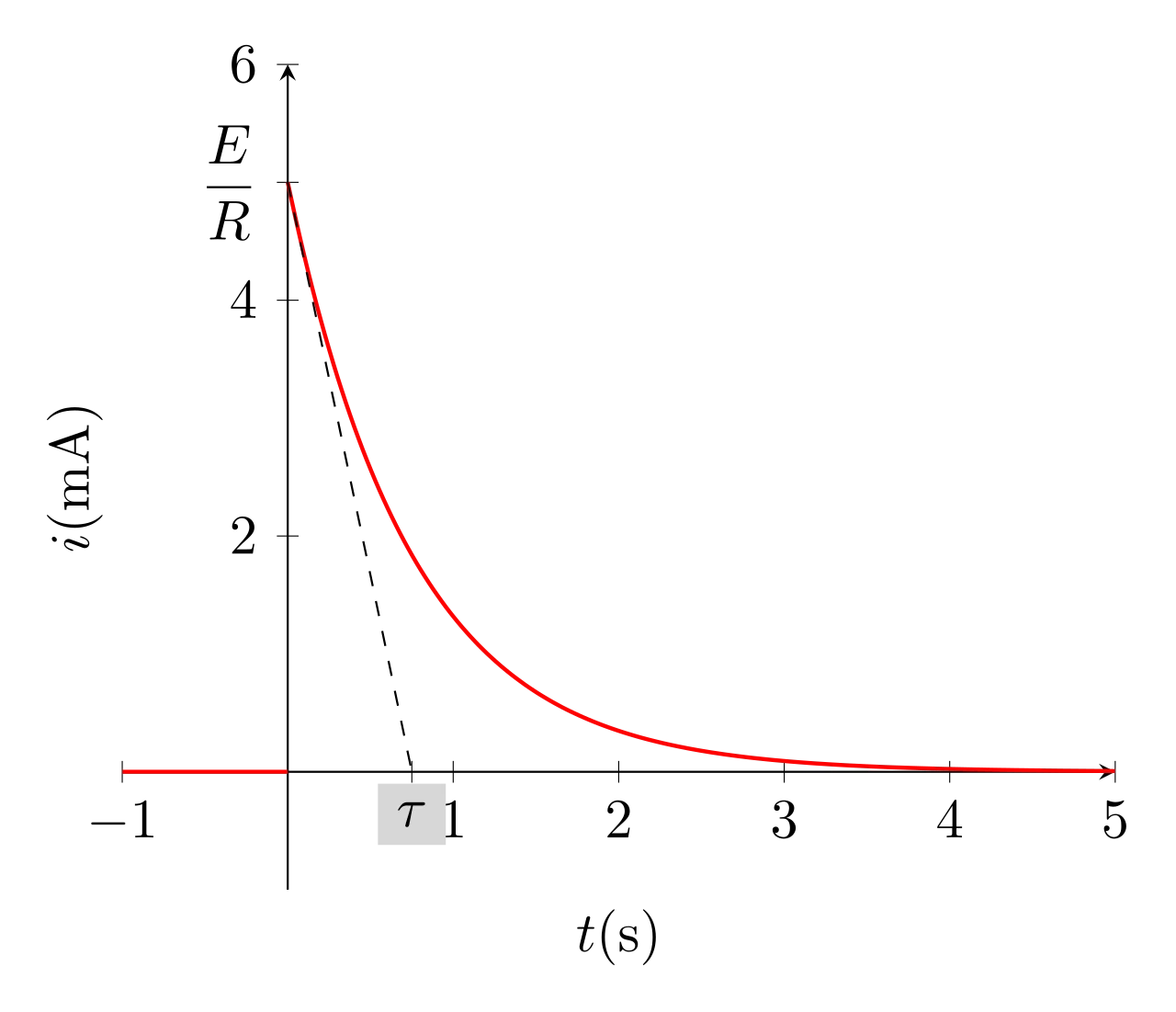
\begin{equation}\boxed{i(t) = \dfrac{E}{R} e^{-\frac{t}{\tau}}}\end{equation}
La fonction \(i(t)\) est discontinue.
Décharge du condensateur
On doit trouver une solution à l’équation : \(\tau \dfrac{du}{dt} + u = 0\).
Solution
On cherche une solution de la forme \(u = A e^{\alpha\,t}\) avec A une constante et \(\alpha\) un réel.
Injectons \(u\) dans l’équation :
\begin{equation}\tau \times \alpha A e^{\alpha\,t} + A e^{\alpha\,t} = 0\end{equation}
Ce qui donne \(\alpha = -\dfrac{1}{\tau}\).
La solution s’écrit donc : \(u(t) = A e^{-\frac{t}{\tau}}\).
Utilisation de la condition initiale
A \(t=0\), \(u(t)=E\) donc \(A =E \).
Finalement, la tension aux bornes du condensateur qui se décharge s’écrit :
\begin{equation}\boxed{u(t) = E e^{-\frac{t}{\tau}}}\end{equation}
Et son allure est représentée ci-contre. On peut vérifier que la fonction \(u(t)\) est bien continue.
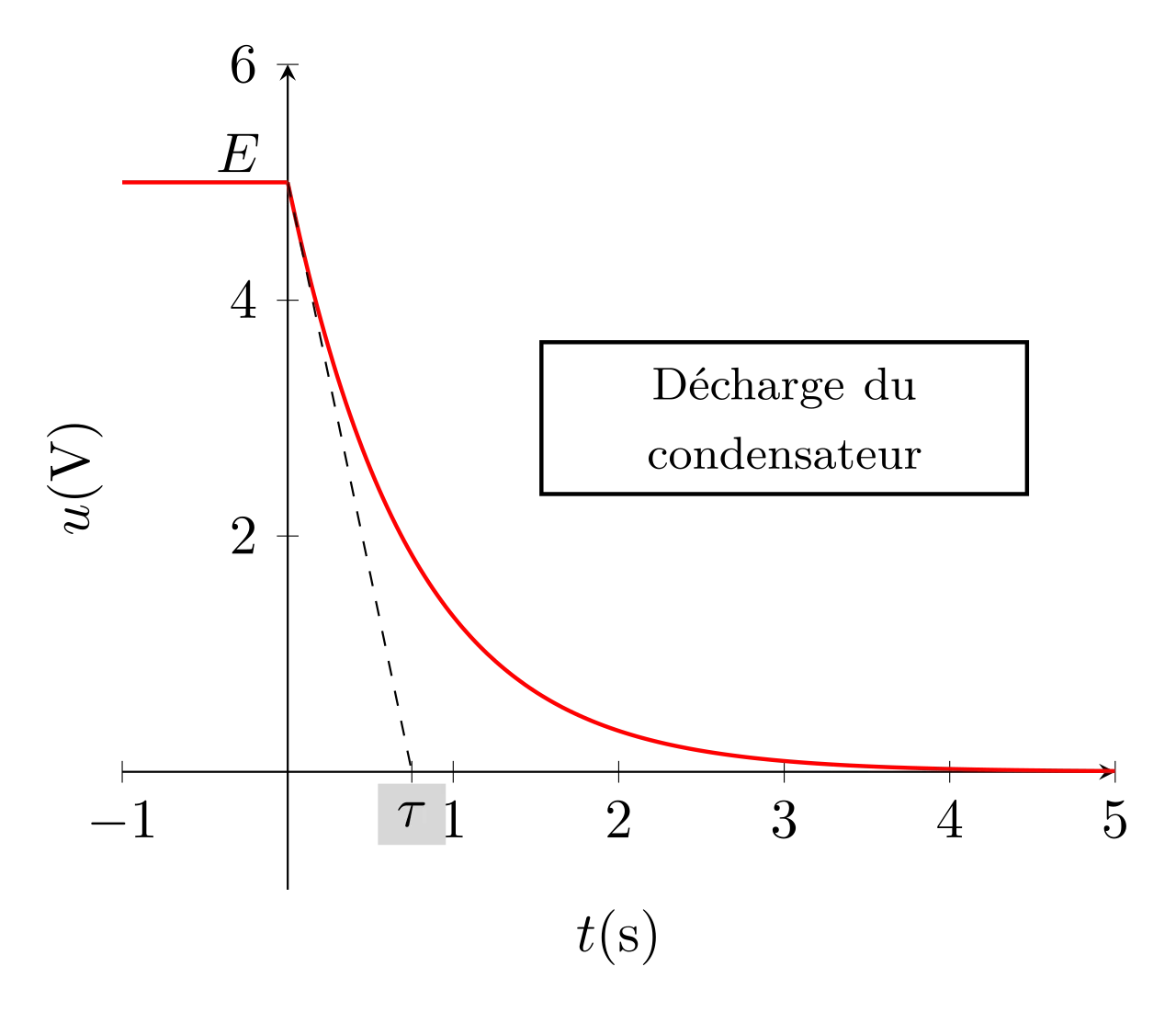
Intensité dans le circuit
On peut facilement obtenir l’équation de l’intensité du courant et son allure.
En effet, \(i =C\dfrac{\mathrm{d}u}{\mathrm{d}t}\) d’où :
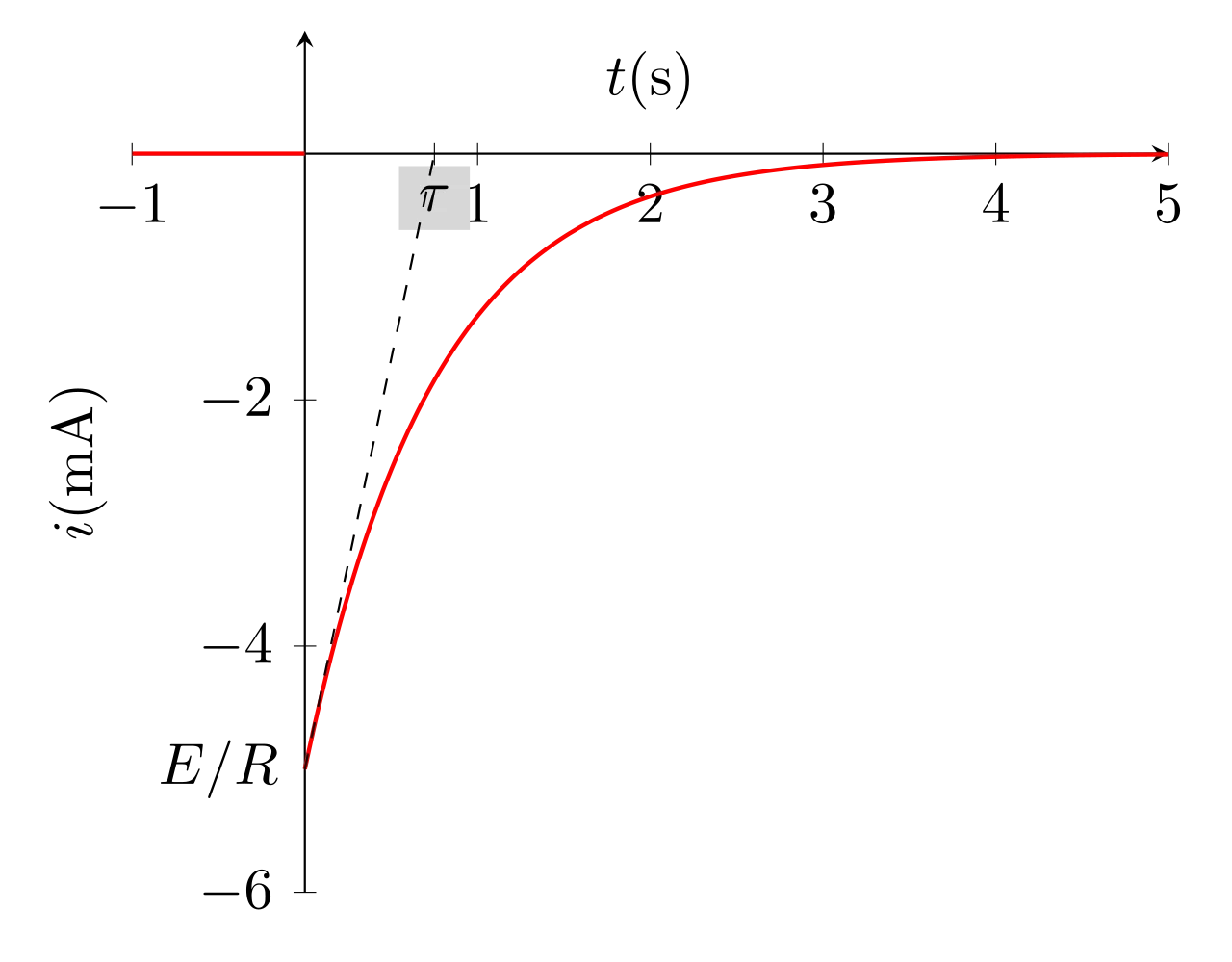
\begin{equation}\boxed{i(t) = - \dfrac{E}{R} e^{-\frac{t}{\tau}}}\end{equation}
La fonction \(i(t)\) est discontinue.
Aspects énergétiques
Cas de la charge
Reprenons la loi des mailles utilisées pour établir l’équation différentielle concernant la tension aux bornes du condensateur dans un circuit RC :
\begin{equation}\begin{aligned} & Ri + u = e(t) \\ \Longleftrightarrow & R\dfrac{\mathrm{d}q}{\mathrm{d}t} + \dfrac{q}{C} = E \hspace{0.5cm} \text{; multiplions cette équation par $i\,\mathrm{d}t$ :}\\ \Longleftrightarrow & Ri^2\,\mathrm{d}t + \dfrac{q}{C}\dfrac{\mathrm{d}q}{\mathrm{d}t}\mathrm{d}t = E\,i\,\mathrm{d}t \\ \Longleftrightarrow & Ri^2\,\mathrm{d}t + d\left(\dfrac{q^2}{2C}\right) = E\,i\,\mathrm{d}t \end{aligned}\end{equation}
On reconnaît alors les énergies suivantes :
La première correspond à l’énergie dissipée par effet Joule dans le conducteur ohmique pendant le temps \(dt\) ;
La deuxième correspond à l’énergie stockée dans le condensateur pendant le temps \(dt\) ;
La troisième correspond à l’énergie fournie par la source de tension pendant le temps \(dt\).
On peut intégrer ces énergies infinitésimales sur le temps de charge du condensateur :
Énergie fournie par le générateur :
\begin{equation}E_g = \int_0^{5\tau} Eidt = E \int_0^Q \mathrm{d}q = EQ = CE^2\end{equation}
car \(i=\dfrac{dq}{dt}\) ; pendant la charge du condensateur ; \(Q=Cu\) et lorsque le condensateur est chargé \(u=E\).
Énergie stockée dans le condensateur :
\begin{equation}E_C = \int_0^Q d\left(\dfrac{q^2}{2C}\right) = \dfrac{Q^2}{2C} = \dfrac{CE^2}{2}\end{equation}
Énergie dissipée par effet Joule : comme la moitié de l’énergie fournie par le générateur est stockée dans le condensateur, cela signifie que l’autre moitié est dissipée par effet Joule dans le conducteur ohmique :
\begin{equation}E_J = \dfrac{CE^2}{2}\end{equation}
Cas de la décharge
A l’issue de la charge, le condensateur qui avait accumulée l’énergie \(\dfrac{CE^2}{2}\) la restitue intégralement au conducteur ohmique qui la dissipe par effet Joule.
Circuit RL
Équation différentielle
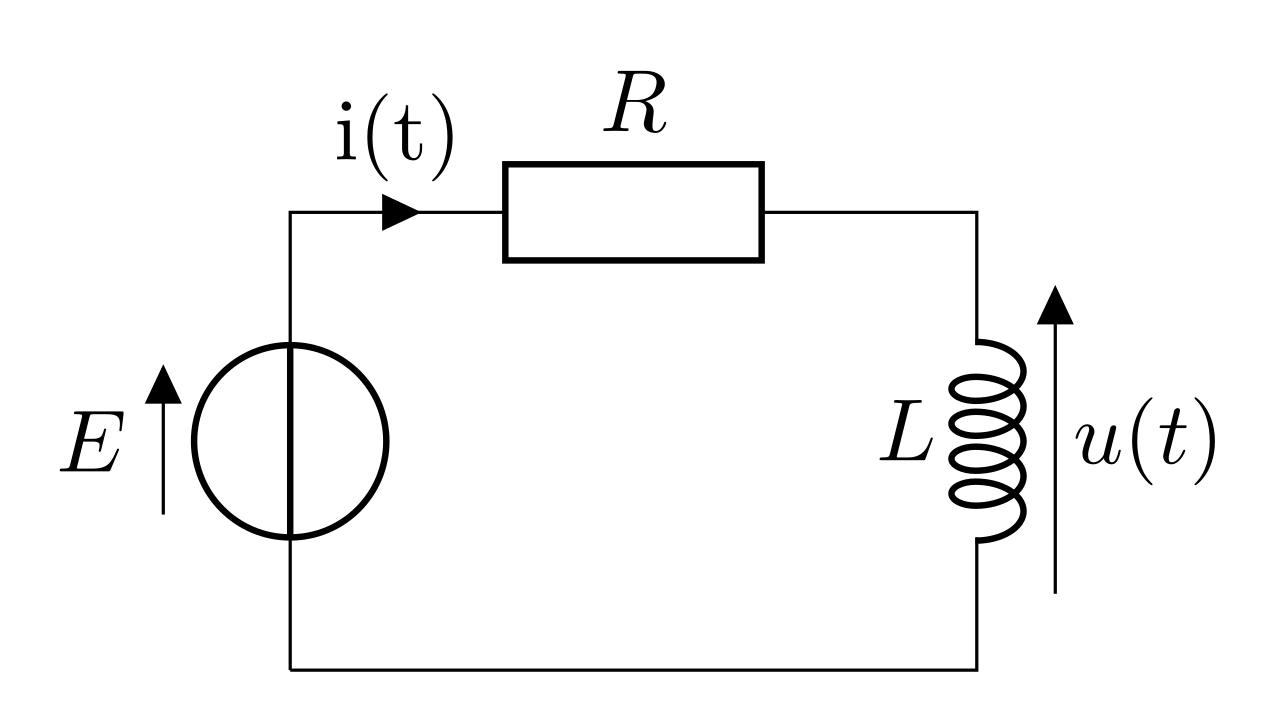
On étudie le circuit RL soumis à une tension \(e(t)\), on s’intéresse à l’allure de l’intensité dans le circuit et à la tension aux bornes de la bobine. On considère de plus que la bobine est idéale (\(r = 0\)). On applique la loi des mailles :
\begin{equation}e(t) = Ri + L\dfrac{\mathrm{d}i}{\mathrm{d}t}\end{equation}
D’où
\begin{equation}\boxed{\tau\dfrac{\mathrm{d}i}{\mathrm{d}t} + i = \dfrac{e(t)}{R}} \end{equation}
avec \(\tau = \dfrac{L}{R}\).
Cette équation différentielle est du premier ordre, le circuit RL est appelé circuit du premier ordre.
Cas de notre étude
La solution de cette équation différentielle sera différente selon le cas étudié.
Pour obtenir la solution la plus générale, on additionne :
une solution de l’équation homogène associée (sans second membre) qui correspond à la réponse du circuit RL sans excitation : c’est ce que l’on appelle le régime libre ;
une solution particulière qui correspond au régime permanent.
On s’intéressera ici au circuit soumis à un échelon de tension, donc la tension e(t) est égale à une constante : E pour l’établissement du courant dans la bobine, 0 pour sa rupture.
Établissement du courant
L’équation différentielle concernant le circuit RL (équation ) a la même forme que celle pour le circuit RC (équation ), la solution de cette équation a la même forme.
On peut donc écrire :
\begin{equation}i(t) = A e^{-\frac{t}{\tau}} + \dfrac{E}{R}\end{equation}
Utilisation de la condition initiale
On sait que \(i(t=0)=0\) soit \(A = -\dfrac{E}{R}\).
La solution s’écrit finalement :
\begin{equation}\boxed{i(t) = \dfrac{E}{R} \left(1 - e^{-\frac{t}{\tau}}\right)}\end{equation}
Et son allure est représentée ci-contre. On peut vérifier que la fonction \(i(t)\) est bien continue.
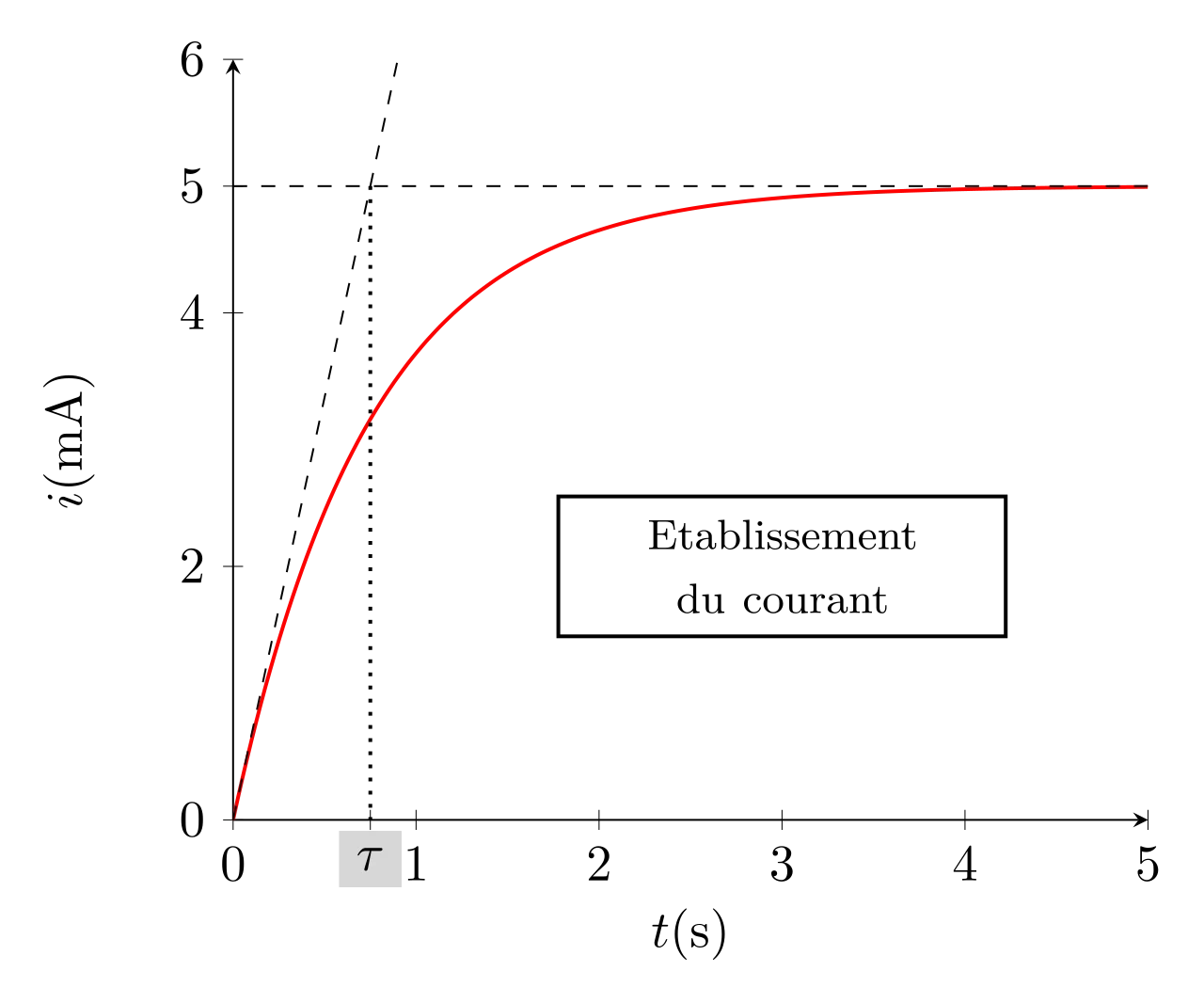
Comme le montre la figure ci-dessus, la constante de temps \(\tau = \dfrac{L}{R}\) peut être facilement obtenue graphiquement. Ce temps permet de caractériser la vitesse d’établissement du courant, plus il est faible plus le courant s’établit vite.
On dit aussi souvent qu’au bout d’un temps t égal à \(5\tau\), on est passé du régime transitoire au régime permanent.
Tension aux bornes de la bobine
On peut facilement obtenir l’équation de la tension aux bornes de la bobine et son allure.
En effet, \(u =L\dfrac{\mathrm{d}i}{\mathrm{d}t}\) d’où :
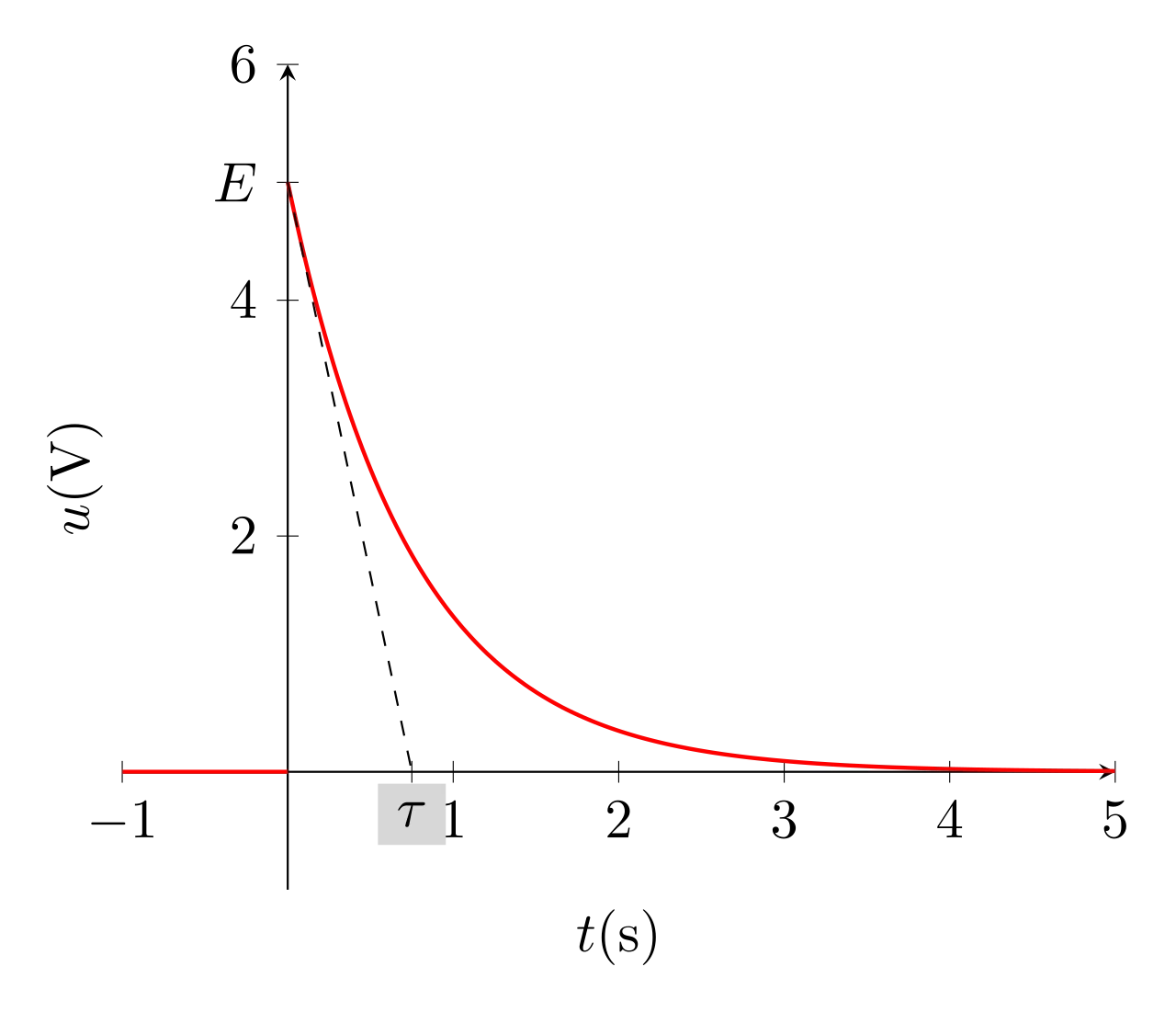
\begin{equation}\boxed{u(t) = E e^{-\frac{t}{\tau}}}\end{equation}
La fonction \(u(t)\) est discontinue.
Rupture du courant
On doit trouver une solution à l’équation : \(\tau \dfrac{\mathrm{d}i}{\mathrm{d}t} + i = 0\).
Cette équation a la même forme que celle qui concerne la tension aux bornes du condensateur lors de sa décharge, la solution possède donc aussi la même forme :
La solution s’écrit donc : \(i(t) = A e^{-\frac{t}{\tau}}\).
Utilisation de la condition initiale
A \(t=0\), \(i(t)=\dfrac{E}{R}\) donc \(A =\dfrac{E}{R}\).
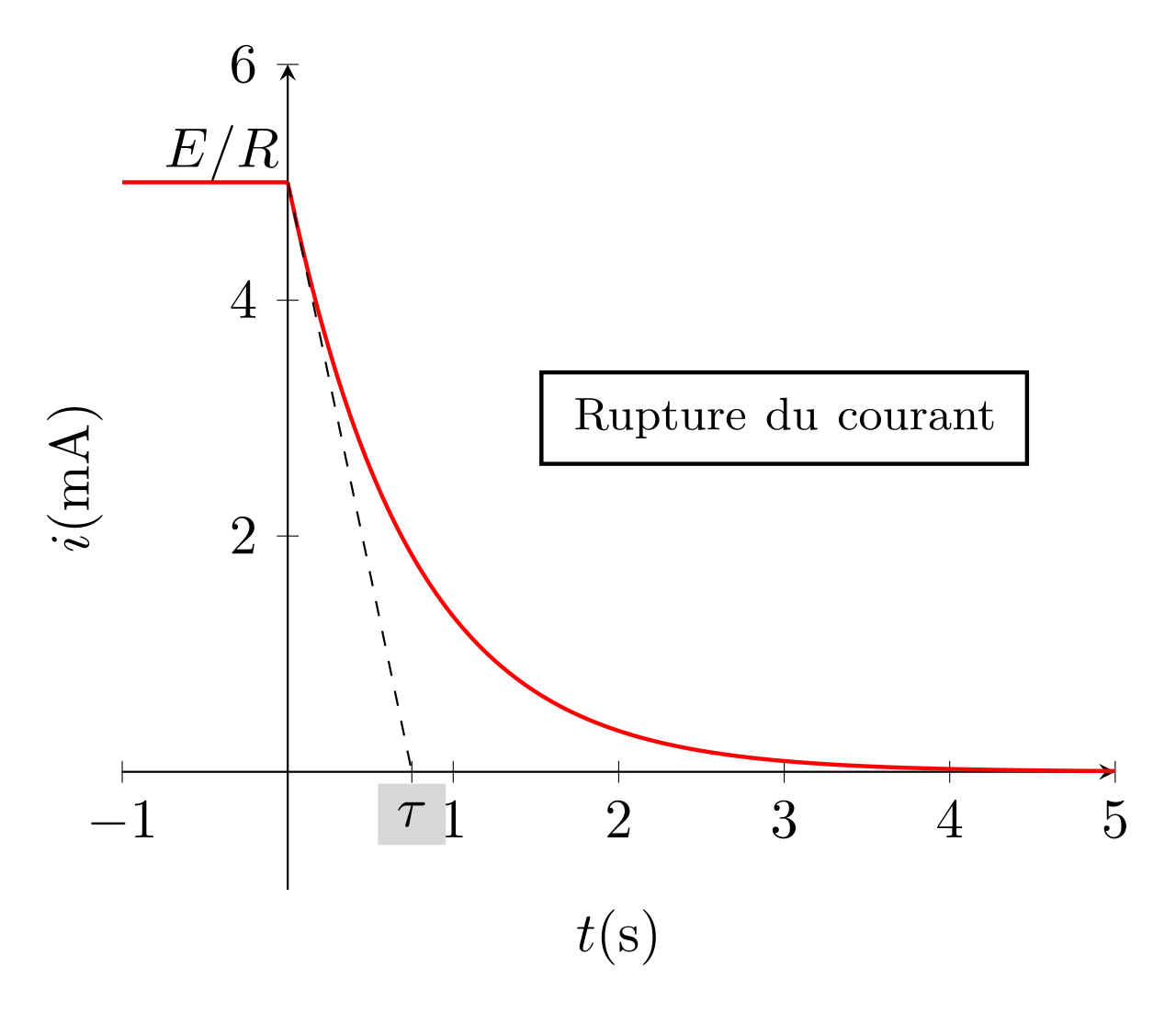
Finalement, l’intensité dans le circuit lors de la rupture du courant s’écrit :
\begin{equation}\boxed{i(t) = \dfrac{E}{R} e^{-\frac{t}{\tau}}}\end{equation}
Et son allure est représentée ci-contre. On peut vérifier que la fonction \(i(t)\) est continue.
Tension aux bornes de la bobine
On peut facilement obtenir l’équation de la tension aux bornes de la bobine et son allure.
En effet, \(u =L\dfrac{\mathrm{d}i}{\mathrm{d}t}\) d’où :
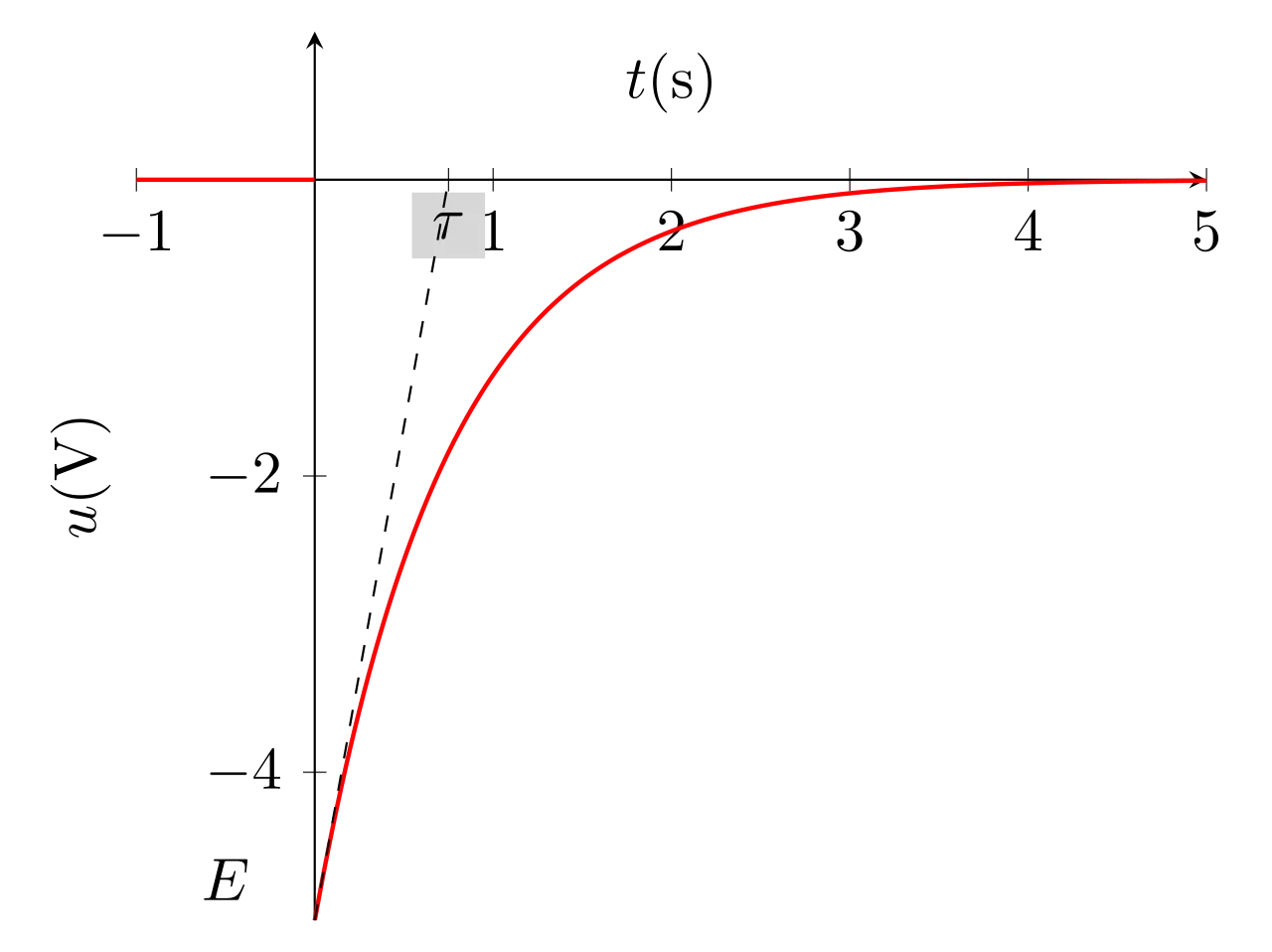
\begin{equation}\boxed{u(t) = - E e^{-\frac{t}{\tau}}}\end{equation}
La fonction \(u(t)\) est discontinue.
Aspects énergétiques
Dans le même principe que ce qui a été fait à propos du circuit RC, on montre que l’énergie que fournit le générateur pendant l’établissement complet du courant se partage par moitié dans la bobine où elle est stockée de façon magnétique, l’autre moitié étant dissipée par effet Joule dans le conducteur ohmique.
A la rupture du courant, la bobine restitue l’énergie précédemment accumulée au conducteur ohmique qui la dissiper une nouvelle fois par effet Joule.
Compléments
Il peut être utile, en parallèle de tout ces aspects théoriques, d'avoir un moyen de simuler le comportement des différents circuits électriques étudiés (l'idéal serait bien sûr de pouvoir expérimenter réellement).
Il existe des simulateurs en ligne Le simulateur en ligne multisim permet cela.
Il est relativement facile de prendre en main ce genre de programme, il faut juste veiller à ce que les composants soient bien connectés, ainsi que les sondes ou appareils de mesures.
Une fois le circuit réalisé, il est possible d'étudier sa réponse en régime transitoire ("transient" en anglais, le sujet de ce cours) ou en régime sinusoïdal ("AC SWEEP" en anglais, sujet du chapitre 4).
Vous pouvez retrouver un TP-cours sur le dipôle RC qui utilise ce simulateur à l'adresse suivante : https://physique.ensc-rennes.fr/tp-cours-dipole-rc.php.
Et aussi un TP-cours sur le dipôle RL suivant le même principe : https://physique.ensc-rennes.fr/tp-cours-dipole-rl.php.


