Licence 1 > Mécanique 1 > Cours 3 : oscillateurs

M13 : oscillateurs

Ce chapitre est disponible en vidéos. La première vidéo de la playlist dédiée est disponible ici :

Vous pouvez également visionner le chapitre séquence par séquence :

1. Plan et force de rappel d'un ressort
2. Equation différentielle, solution, ressort vertical
3. Pendule simple : position, vitesse et accélération en coordonnées polaires
4. Application du PFD sur le pendule simple, solution mathématique et graphique
5. Système solide-ressort avec frottements fluides : différents régimes.

Introduction

Nous étudierons dans ce chapitre en premier lieu l’oscillateur harmonique solide-ressort horizontale, nous introduirons donc la force de rappel du ressort et nous découvrirons l’équation différentielle de l’oscillateur harmonique et sa solution.L’oscillateur solide-ressort vertical sera ensuite abordé : tout d’abord, ce sera l’occasion de retrouver l’équation différentielle de l’oscillateur harmonique, puis nous introduirons des frottements fluides pour voir le comportement du système. Enfin, nous aborderons un oscillateur à deux dimensions, le pendule simple. Cela permettra l’introduction de la base de projection polaire.

Système solide-ressort horizontal sans frottement

Problème 4

Soit un point M de masse \(m\) accroché à l’extrémité d’un ressort horizontal sans masse. Le point M se déplace sans frottement sur le plan horizontal. A \(t=0\), on écarte ce point de sa position d’équilibre d’une grandeur \(x_m\) puis on le lâche sans vitesse initiale. Quel est son mouvement, quels sont ses caractéristiques ?

Système

Le point M de masse \(m\).

Référentiel et base de projection

Référentiel lié au plan horizontal sur lequel se déplace le point M, référentiel terrestre considéré comme galiléen. On prendra une base cartésienne à une dimension : un axe Ox horizontal permettra de repérer le point M.

Bilan des forces

Le point M est soumis :

• à son poids \(\overrightarrow{P}\), force verticale vers le bas;
• à la réaction du support, réaction verticale vers le haut car il n’y a pas de frottement avec le plan horizontal.
• à la force de rappel du ressort, force horizontale. Pour connaitre son expression, observons deux situations :

Cette force est proportionnelle à l'allongement du ressort et à une constante qui caractérise la raideur du ressort, $k$ appelée constante de raideur. L'allongement du ressort à un instant $t$ est défini par :

\begin{equation} \mathrm{allongement} = \ell - \ell_0 \Longrightarrow F_\mathrm{rappel} = k\times \mathrm{allongement} \end{equation}

Si $\ell$ est la longueur du ressort à l'instant $t$ et $\ell_0$ sa longueur à vide c'est à dire au repos.

Observons deux situations pour connaître l'expression vectorielle de la force de rappel du ressort :

2ème Loi de Newton : obtention de l’équation différentielle

Appliquions la deuxième loi de Newton puis projetons-la sur la base de projection choisie :

\begin{equation}\begin{aligned} \sum \overrightarrow{F_{\mathrm{ext}}} = m\,\overrightarrow{a} &\Longrightarrow \overrightarrow{P} + \overrightarrow{R} + \overrightarrow{F} = m\,\overrightarrow{a} \\ \text{projection suivant Ox} &\Longrightarrow -k\,x = m\,\ddot x \\ & \Longleftrightarrow \boxed{\ddot x + \dfrac{k}{m}\,x = 0}\end{aligned}\end{equation}

Solution de l’équation différentielle : oscillations harmoniques et caractéristiques

Notion de pulsation

L’équation différentielle précédente s’écrit généralement de la manière suivante :

\begin{equation}\boxed{ \ddot x + \omega_0^2\,x = 0 }\end{equation}

avec \(\omega_0\) nommée pulsation propre.

Expression de la solution

Mathématiquement, cette équation a pour solution une fonction sinusoïdale :

\begin{equation}x(t) = A\,\cos\,(\omega_0\,t + \phi)\end{equation}

où \(A\) et \(\phi\) sont des constantes déterminées à partir des conditions initiale. \(A\) est appelé amplitude et s’exprime en mètre (m) et \(\phi\) phase à l’origine exprimée en radian (rad).

Utilisation des conditions initiales

• A \(t=0\), \(x(t=0) = x_m \Longrightarrow A\,\cos\,\phi = x_m\)
• On a : \(v(t) = -\omega_0\,A\,\sin\,(\omega_0\,t + \phi)\) Alors à \(t=0\), \(v(t=0) = -\omega_0\,A\,\sin\,(\phi) = 0\).\(A\) et \(\omega_0\) ne peuvent être nuls donc \(\sin\,\phi = 0 \Longrightarrow \boxed{\phi = O\; \left[\pi\right]}\). Et finalement \(\boxed{A = x_m}\).

La solution s’écrit donc :

\begin{equation}\boxed{x(t) = x_m\,\cos\,\omega_0\,t}\end{equation}

Allure de la solution

Système solide-ressort vertical sans frottement

Problème 5

Soit un point M de masse \(m\) accroché à l’extrémité d’un ressort vertical sans masse. A \(t=0\), on écarte ce point de sa position d’équilibre d’une grandeur \(x_m\) puis on le lâche sans vitesse initiale. Quel est son mouvement, quels sont ses caractéristiques?

Résolution

Le système est toujours le point M de masse \(m\), le référentiel toujours terrestre et galiléen et le bilan des forces est identique. On choisira aussi une base cartésienne à une dimension, un axe Ox, vertical descendant.

PFD appliqué à la masse et projeté sur l’axe O$x$:

\begin{equation}\begin{aligned} m\,\ddot x&=m\,g - k\,(\ell-\ell_0) \\ \Longleftrightarrow m\,\ddot x &=m\,g - k\,(x+\ell_{éq}-\ell_0) \\ \Longleftrightarrow m\,\ddot x &=m\,g - k\,x -k\,(\ell_{éq}-\ell_0) \end{aligned}\end{equation}

Or à l’équilibre :

\begin{equation}m\,g - k\,(\ell_{éq}-\ell_0) = 0\end{equation}

Donc devient :

\begin{equation}m\,\ddot x =- k\,x \Longleftrightarrow \boxed{\ddot x +\dfrac{k}{m}x = 0}\end{equation}

On retrouve donc la même équation que celle obtenue pour le ressort horizontal, la solution sera identique ... On peut reprendre à ce niveau tout le paragraphe [solution].

Pendule simple

Problème 6

Un enfant, assimilé à un point matériel M de masse \(m\), est assis sur une balançoire. Les cordes de la balançoire sont inextensibles, de longueur \(\ell\) et n’ont pas de masse. Un adulte écarte d’un petit angle l’enfant de sa position d’équilibre puis la lâche sans vitesse initiale. On néglige tous les frottements.Quel est le mouvement de l’enfant? les caractéristiques de celui-ci?

Système

L’enfant de masse \(m\).

Référentiel et base

Référentiel

On choisira un référentiel lié à un observateur posé, par exemple, sur le support de la balançoire. C’est un référentiel terrestre supposé galiléen le temps du mouvement de l’enfant.

Base : présentation de la base polaire

Lorsque l’on a à faire à un mouvement de rotation autour d’un axe fixe, par exemple lorsque le solide en mouvement peut être repéré facilement par un angle ; l’utilisation de la base polaire (2D) est judicieuse.

Liens entre la base polaire et la base cartésienne à deux dimensions

Comme le montre les pointillés sur la figure ci-dessus, il est facile de passer de la base polaire à la base cartésienne et inversement :

De la même manière, les vecteurs unitaires (\(\overrightarrow{u}_r\); \(\overrightarrow{u}_{\theta}\)) peuvent s’exprimer en fonction des vecteurs unitaires de la base cartésienne (\(\overrightarrow{u}_x\); \(\overrightarrow{u}_y\)) :

\begin{equation}\boxed{ \overrightarrow{u}_r = \cos\,\theta\,\overrightarrow{u}_x + \sin\,\theta\,\overrightarrow{u}_y \qquad \qquad \overrightarrow{u}_{\theta} = -\sin\,\theta\,\overrightarrow{u}_x + \cos\,\theta\,\overrightarrow{u}_y } \end{equation}

Position, vitesse, accélération en base polaire

La difficulté par rapport au travail avec une base cartésienne est que les vecteur de la base polaire sont mobiles, ils sont donc une dérivée par rapport au temps qui est non nulle.

• Vecteur position :
  \begin{equation}\boxed{\overrightarrow{OM} = \ell\,\overrightarrow{u}_r}\end{equation}
• Vecteur vitesse :
  \begin{equation}\overrightarrow{v} = \dfrac{\mathrm{d}\overrightarrow{OM}}{\mathrm{d}t} = \dfrac{\mathrm{d}(\ell\,\overrightarrow{u}_r)}{\mathrm{d}t} = \dfrac{\mathrm{d}\ell}{\mathrm{d}t}\,\overrightarrow{u}_r+\ell\,\dfrac{\mathrm{d}\overrightarrow{u}_r}{\mathrm{d}t}\end{equation}

  Regardons ce que vaut \(\dfrac{\mathrm{d}\overrightarrow{u}_r}{\mathrm{d}t}\) :

  \begin{equation}\dfrac{\mathrm{d}\overrightarrow{u}_r}{\mathrm{d}t} = \dfrac{\mathrm{d}\overrightarrow{u}_r}{\mathrm{d}\theta} \times \dfrac{\mathrm{d}\theta}{\mathrm{d}t} = \dfrac{\mathrm{d}\overrightarrow{u}_r}{\mathrm{d}\theta} \times \dot \theta\end{equation}

  Or d’après la relation (17) :

  \begin{equation}\dfrac{\mathrm{d}\overrightarrow{u}_r}{\mathrm{d}\theta} = -\sin\,\theta\,\overrightarrow{u}_x + \cos\,\theta\,\overrightarrow{u}_y = \overrightarrow{u}_{\theta}\end{equation}

  Donc :

  \begin{equation}\dfrac{\mathrm{d}\overrightarrow{u}_r}{\mathrm{d}t} = \dot \theta \, \overrightarrow{u}_{\theta}\end{equation}

  Et :

  \begin{equation}\boxed{\overrightarrow{v} = \dot \ell\,\overrightarrow{u}_r + \ell\,\dot \theta\,\overrightarrow{u}_{\theta}}\end{equation}

  Remarque
  La grandeur \(\dfrac{\mathrm{d}\theta}{\mathrm{d}t} = \dot \theta\) pourra être notée \(\omega\) et être appelée vitesse angulaire.

• Vecteur accélération :
  \begin{equation}\overrightarrow{a} = \dfrac{\mathrm{d}v}{\mathrm{d}t} = \dfrac{\mathrm{d}^2 \overrightarrow{OM}}{\mathrm{d}t^2}\end{equation}

  On procède de la même manière que pour le vecteur vitesse pour obtenir :

  \begin{equation}\boxed{\overrightarrow{a} = (\ddot \ell - \ell\,\dot \theta^2)\overrightarrow{u}_r + (2\,\dot \ell\,\dot \theta + \ell\,\ddot \theta) \overrightarrow{u}_{\theta}}\end{equation}

Bilan des forces

Deuxième loi de Newton

On applique le PFD au point M, on le projette sur la base polaire (\(\overrightarrow{u}_r\), \(\overrightarrow{u}_{\theta}\)):

\begin{equation}\sum \overrightarrow{F_{\mathrm{ext}}} =\overrightarrow{P} + \overrightarrow{T} = m\,\overrightarrow{a} \Longrightarrow \left\{\begin{array}{l} \text{Sur}\,\overrightarrow{u}_r :\quad m\,g\,\cos\,\theta - T = m(\ddot \ell - \ell \dot \theta^2) \\ \text{Sur}\,\overrightarrow{u}_{\theta} :\quad -m\,g\,\sin\,\theta = m(2\,\dot\ell \dot \theta + \ell\,\ddot \theta) \end{array}\right.\end{equation}

Equation différentielle du mouvement

Mais le fil est inextensible : \(\dot \ell = 0\), d’où:

\begin{equation}\left\{\begin{array}{l} \text{Sur}\,\overrightarrow{u}_r :\quad m\,g\,\cos\,\theta - T = - m\,\ell \dot \theta^2 \\ \text{Sur}\,\overrightarrow{u}_{\theta} :\quad -m\,g\,\sin\,\theta = m\,\ell\,\ddot \theta \end{array}\right.\end{equation}

La première équation est celle qui décrit le mouvement de l’enfant, la deuxième donne la tension du fil en fonction de l’angle \(\theta\).

Enfin, on se place dans l’approximation des petites angles, \(\theta\) est petit et \(\sin\,\theta \simeq \theta\). Alors :

\begin{equation}\boxed{ \ddot \theta + \dfrac{g}{\ell}\,\theta = 0}\end{equation}

Solution

L’équation obtenue précédemment ressemble étrangement à celle du pendule élastique. La solution s’écrit :

\begin{equation}\boxed{\theta = \theta_m\,\cos\,(\omega_0\,t + \phi) \qquad \text{avec } \omega_0 = \dfrac{2\,\pi}{T_0} = \sqrt{\dfrac{g}{\ell}}}\end{equation}

avec \(\theta_m\) et \(\phi\) des constantes déterminées grâce aux conditions initiales.

L’enfant oscille donc indéfiniment (pas de frottement) à la période :

\begin{equation}\boxed{ T_0 = 2\pi \sqrt{\dfrac{\ell}{g}}}\end{equation}

Le pendule simple est un oscillateur harmonique.

Système solide-ressort avec frottements fluides

Problème 7

On reprend l’exemple des oscillateurs précédents : système masse-ressort horizontal ou vertical, ou balançoire. Mais cette fois-ci, des frottements fluides viennent freiner le point M dans son mouvement.Comment ce mouvement est-il modifié? quelles sont ces nouvelles caractéristiques?

Equation différentielle

La masse accrochée au ressort est maintenant soumise en plus des forces déjà évoquées à une force de frottement fluide d’expression \(\overrightarrow{f}=-\alpha\,\overrightarrow{v}\) (le \(k\) est déjà pris, nous sommes dans le cas de petites vitesses donc de frottements linéaires). L’équation différentielle (issue du PFD appliqué à la masse et projeté sur un axe colinéaire au ressort) qui régit l’oscillation de la masse s’obtient de la façon suivante :

\begin{equation}\begin{aligned} \text{PFD :} \quad &\overrightarrow{P} + \overrightarrow{R} + \overrightarrow{f} + \overrightarrow{T} = m\,\overrightarrow{a} \\ \text{Projection}\; \Longrightarrow \;& m\,\ddot x = -k\,x -\alpha\,\dot x \\ \Longleftrightarrow \;&\boxed{\ddot x + \dfrac{\alpha}{m}\,\dot x + \dfrac{k}{m}\,x = 0} \end{aligned}\end{equation}

Cete équation différentielle peut se noter de trois façons différents, qui font intervenir différentes grandeurs caractéristiques du système :

• On continuera à utiliser la pulsation des oscillations \(\omega_0 = \dfrac{k}{m}\) et on introduit un autre facteur, \(\lambda = \dfrac{\alpha}{2m}\). L’équation s’écrit alors :
  \begin{equation}\ddot x + 2\,\lambda\,\dot x + \omega_0^2\,x = 0\end{equation}
• Mais on pourra aussi introduire un temps \(\tau\) (qui sera caractéristique de l’évolution du système) définit par \( \boxed{\tau = \dfrac{m}{\alpha} = \dfrac{1}{2\,\lambda}} \) dans l’équation différentielle :
  \begin{equation}\ddot x + \dfrac{\dot x}{\tau} + \omega_0^2\,x = 0\end{equation}
• Enfin, il est possible d’introduire le facteur de qualité définit par \(\boxed{Q = \omega_0\,\tau}\) :
  \begin{equation}\ddot x + \dfrac{\omega_0}{Q}\,\dot x + \omega_0^2\,x = 0\end{equation}

Solution de l’équation différentielle : différents régimes

Equation caractéristique

Une équation différentielle du type de l’équation se résout à partir de son équation caractéristique :

\begin{equation}\ddot x + 2\,\lambda\,\dot x + \omega_0^2\,x = 0 \Longrightarrow \boxed{r^2 + 2\,\lambda\,r + \omega_0^2 = 0}\end{equation}

Solution

A partir des racines \(r_1\) et \(r_2\) de l’équation caractéristique, on construit la solution de la manière suivante :

\begin{equation}x(t) = A\,\times e^{(r_1\,t)} + B\,\times e^{(r_2\,t)}\end{equation}

La nature de \(r_1\) et \(r_2\) et de \(A\) et \(B\) dépend du signe du déterminant de l’équation caractéristique : selon ce signe, on obtient différents régimes.

Régime pseudo-périodique

Solution

Dans ce cas le discriminant est négatif :

\begin{equation}\Delta = 4\,\lambda^2 - 4\,\omega_0^2 < 0 \Longleftrightarrow \boxed{\lambda < \omega_0 \Longleftrightarrow Q > \dfrac{1}{2}}\end{equation}

Et les deux racines de l’équation caractéristique \(r_1\) et \(r_2\) sont complexes, conjuguées entre elles :

\begin{equation}r_{\pm} = -\lambda \pm j\,\sqrt{\omega_0^2-\lambda^2} = -\lambda \pm j\,\omega\end{equation}

Remarque
En physique, mais surtout en électricité, le nombre complexe est noté \(j\) (\(j^2 = -1\))

Le paramètre \(\omega\) est appelé pseudo-pulsation des oscillations.

En effet, la solution \(x(t)\) dans le cas du régime pseudo-périodique s’écrit :

\begin{equation}\boxed{ x(t) = X\, e^{(-\lambda\,t)}\,\cos\,(\omega\,t+\phi)}\end{equation}

Avec \(X\) et \(\phi\) des constantes déterminées à l’aide des conditions initiales (de position et de vitesse).

Remarque
On trouvera aussi une solution de forme suivante :

\begin{equation}x(t) = e^{(-\lambda\,t)}\,(A\,\cos\,(\omega\,t) + B\,\sin\,(\omega\,t))\end{equation}

Allure de cette solution

Les oscillations ont alors l’allure suivante :

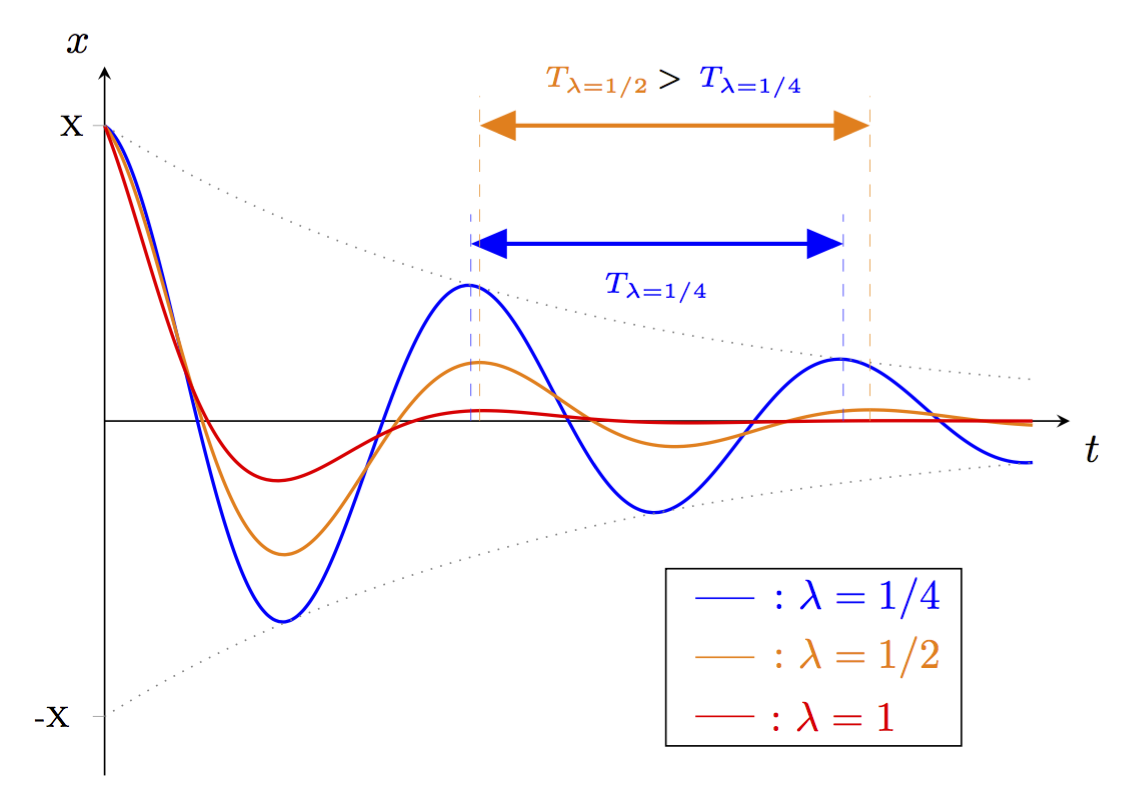
Ces oscillations sont caractérisées par la pseudo-pulsation \(\omega = \sqrt{\omega_0^2-\lambda^2}\), donc une pseudo-période égale à \(T = \dfrac{2\pi}{\sqrt{\omega_0^2-\lambda^2}}\). Cette pseudo-période est souvent proche (amortissement faible) de la période propre de l’oscillateur, mais elle est légèrement plus grande.

Décrément logarithmique

Une autre grandeur que la pseudo-période permet de caractériser ces oscillations, il s’agit du décrément logarithmique qui permet de quantifier l’amortissement des oscillations, leur décroissance. Il est définit par :

\begin{equation}\delta = \ln\,\dfrac{A(t)}{A(t+T)}\end{equation}

où A représente l’amplitude des oscillations. Généralement pour le calculer, on prend deux maximas successifs de la courbe \(x(t)\).On peut également montrer (à partir de l’expression de \(x(t)\)) que \(\delta = \lambda\,T\).

Régime apériodique

Solution

Ici, le discriminant est positif :

\begin{equation}\Delta = 4\,\lambda^2 - 4\,\omega_0^2 > 0 \Longleftrightarrow \boxed{\lambda > \omega_0 \Longleftrightarrow Q < \dfrac{1}{2}}\end{equation}

Les deux racines de l’équation caractéristique sont réelles et opposées :

\begin{equation}r_{\pm} = - \lambda \pm \sqrt{\lambda^2-\omega_0^2}\end{equation}

Dans ce cas, la solution s’écrit :

\begin{equation}x(t) = A\,\times e^(r_{-}\,t) + B\,\times e^(r_{+}\,t)\end{equation}

C’est à dire la somme de deux exponentielles décroissantes car les solutions \(r_{\pm}\) sont négatives (\(\sqrt{\lambda^2-\omega_0^2} < \lambda\)).

Il n’y a pas d’oscillations d’où un régime nommé apériodique.

Allure

Régime critique

Ce régime s’obtient lorsque le discriminant de l’équation caractéristique associé à l’équation différentielle vaut 0. On alors \(\lambda = \omega_0\) et \(Q = \dfrac{1}{2}\). Ce régime est celui qui permet à l’oscillateur de revenir le plus rapidement à l’équilibre. Son allure est la même que celle d’un régime apériodique.

Références

• "Physique Tout-en-un MPSI PCSI PTSI" - Marie-Noëlle Sanz / Anne-Emmanuelle Badel / François Clausset - Editions Dunod 2008 ;