Collège/Lycée > Révisez votre cours
Seconde-Physique-chap 1 :
L'échelle des longueurs
Pour rechercher un mot dans la page, utilisez la fonction de votre navigateur
(Ctrl + F)
- Connaissez-vous les multiples et sous-multiples du mètre avec les symboles et les noms adéquats ?
Remplissez les tableaux ci-dessous :
- Pour les multiples :
Nom Valeur Symbole Kilomètre 103 m Km Megamètre 106 m Mm Gigamètre 109 m Gm Teramètre 1012 m Tm - Pour les sous-multiples :
Nom Valeur Symbole millimètre 10-3 m mm micromètre 10-6 m μm nanomètre 10-9 m nm picomètre 10-12 m pm femtomètre 10-15 m fm
- Pour les multiples :
- Etes-vous capable d'écrire des nombres en notation scientifique :
123 ; 4586,7*102 ; 0,086 ?
- Un nombre écrit en notation scientifique est de la forme a*10n avec 1 < a < 9 et n un entier relatif (positif ou négatif).
- 123 = 1.23*102.
- 4586.7*102 = 4.5867*103*102 = 4.5867*105.
- 0,086 = 8.6*10-2.
- Qu'est-ce qu'un ordre de grandeur ? Etes-vous capable de donner l'ordre de grandeur de la taille d'un atome, d'une fourmi ...
- Un ordre de grandeur est exprimée à l'aide d'une puissance de dix. Il permet de retenir facilement la taille d'un objet par exemple.
- L'ordre de grandeur de la taille de l'atome est 10-10 m.
- L'ordre de grandeur de la taille d'une fourmi est 10-2 m (une fourmi mesure environ entre 5 et 10 mm, on arrondi à la puissance de dix supérieure).
- Etes-vous capable de classer des nombres dans l'ordre croissant (du plus petit au plus grand) :
A = 1.7m ; B = 5mm ; C = 380 000Km ; D = 4807m ; E = 12µm ; F = 860Km
Il est judicieux de s'aider à l'aide d'un axe gradué en puissance de 10.
- Il faut tout d'abord convertir ces nombres dans la même unité, et dans la mesure du possible les écrire en notation scientifique :
A = 1.7m = 1.7*100m
B = 5mm = 5*10-3m
C = 380 000Km = 3.80000*105*103m = = 3.80000*108m
D = 4807m = 4.807*103m
E = 12µm = 1.2*101µm = 1.2*101*10-6m = 1.2*10-5m
F = 860Km = 8.60*102Km = 8.60*102*103m = 8.60*105m - Ensuite le plus facile pour les classer est de les placer sur un axe gradué en puissance de dix :
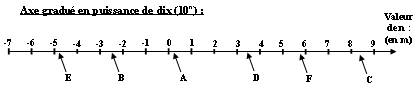
- Il faut tout d'abord convertir ces nombres dans la même unité, et dans la mesure du possible les écrire en notation scientifique :
Questions en relation avec les travaux pratiques (plus difficiles):
- Qu'est-ce que l'incertitude absolue d'une mesure ?
Exemple : on mesure avec un double décimètre l'épaisseur d'un stylo : e = 1.2 cmL'incertitude absolue (Δe) d'une mesure est donnée par l'instrument de mesure, elle est égale à la moitié du dernier rang affiché par l'instrument :
La plus petite unité affichée par la règle est 0.1cm donc l'incertitude absolue sur une mesure à la règle est Δe = 0.1/2 = 0.05cm. - L'incertitude absolue permet alors de donner un encadrement de la mesure effectuée.
Encadrez la mesure e =1.2cm effectuée à la règle graduée.
- Pour encadrer la mesure on procède ainsi : e-Δe < e < e-Δe
- Donc ici : 1.2 - 0.05 = 1.15 < e = 1.2 < 1.25 = 1.2 + 0.05
- Qu'est-ce que l'incertitude relative d'une mesure ? Par quoi s'exprime t-elle ? Calculez l'incertitude correspondant à notre mesure de 1.2cm à la règle graduée.
- L'incertitude relative se calcule par la formule Δe/e.
En effet, cette incertitude est relative à la mesure que l'on effectue. - L'incertitude s'exprime par un pourcentage (on multipliera alors le résultat de la formule ci-dessus par 100.
- Donc ici : Δe/e * 100 = 0.05/1.2 * 100 = 4 % d'incertitude relative.
- L'incertitude relative se calcule par la formule Δe/e.
- Quel est le lien entre la précision d'une mesure et l'incertitude relative sur celle-ci ?
Plus l'incertitude relative est faible, plus la mesure effectuée est précise.


