Agrégation/Capes > Capes : montages de chimie > capes-chimie-montage-9-equilibre

CAPES-Montage chimie n°9 :
Expériences illustrant la notion d'équilibre en solution aqueuse

Pour rechercher un mot dans la page, utilisez la fonction de votre navigateur
(Ctrl + F)

Introduction :

Il existe 4 types principaux d'équilibres chimiques : acido-basique, oxydoréducteur, de précipitation, de complexation.
On peut les mettre en relation en effectuant des analogies entre chaque constituant de ses différents équilibres : donneur-accepteur-particule échangée.

Mise en évidence de quelques équilibres :

Equilibre acido-basique :

On étudie la réaction suivante :

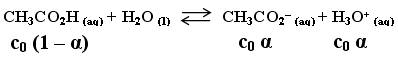
On part d'une solution à c₀ = 1.0*10^-2 mol/L.
Prenons le pH de la solution et avec celui-ci, trouvons la valeur du coefficient de dissociation :
pH = 3.5 or α = 10^-pH/c₀ = 10^-3.5/1.0*10^-2 = 3.4*10^-2

Ainsi on peut avoir :
[CH₃CO₂^-_(aq)] = c₀ * α = 3.4*10^-4 mol/L
[CH₃CO₂H_(aq)] = c₀ * (1 - α) = 9.7*10^-3 mol/L

Cl : La concentration de l'acide éthanoïque n'est pas négligeable, donc l'acide éthanoïque n'est pas totalement dissocié.

Equilibre de précipitation :

On étudie la réaction suivante :

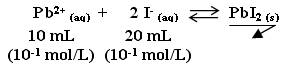
le précipité de PbI₂ est jaune

On choisit les volumes et les concentrations ainsi car il faut veiller à avoir la même quantité d'ions plomb que d'ions iodure.

On filtre le précipité obtenu, puis on vérifie que le filtrat contient les deux types d'ions :

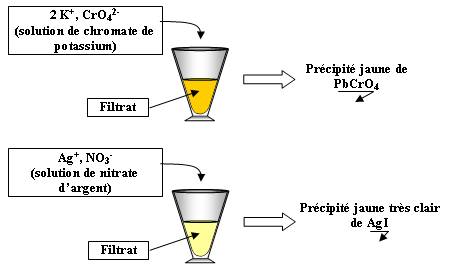
Cl : Il y avait coexistence dans le récipient de départ du précipité PbI, des ions plomb et des ions iodures, cette réaction conduit bien à un équilibre.

Equilibre de complexation :

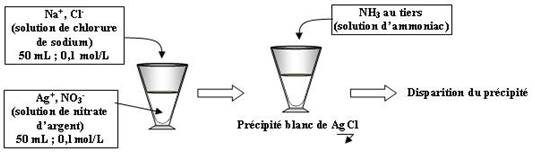
Voici les équations des réactions :

Après la précipitation du chlorure d'argent, l'ajout d'ammoniac forme le complexe Ag(NH₃)₂⁺ qui fait disparaître AgCl.
Si ensuite on ajoute des ions iodure I^-_(aq) (avec une solution d'iodure de potassium par exemple), il y a précipitation de AgI_(s) ce qui prouve la présence des ions argent Ag⁺_(aq).

Cl : S' il y a présence du complexe et des ions argent, l'ammoniac NH_3(aq) est forcément présent : nous sommes en présence d'un équilibre de complexation.

Equilibre d'oxydoréduction :

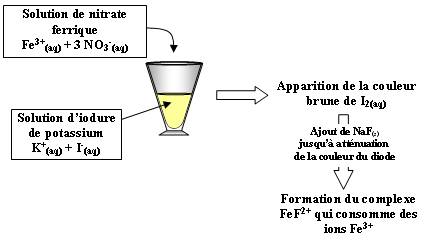
Voici l'équation de la réaction :

2 Fe³⁺_(aq) + 2 I^-_(aq) 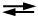2 Fe²⁺_(aq) + I_2(aq)

Cl :

• On a Fe³⁺_(aq) et I₂ en présence donc équilibre.
• Le complexe qui se forme entre les ions fluorure et les ions ferrique (FeF²⁺) déplace l'équilibre vers la gauche car il y a consommation d'ions ferrique.
• Ce complexe abaisse le potentiel d'oxydoréduction du couple Fe³⁺_(aq)/Fe²⁺_(aq) :
  

Détermination des constantes d'équilibre :

Constante d'acidité K_A :

Revenons sur l'expérience I1), la constante d'acidité s'écrit :

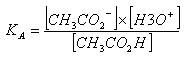
Avec le calcul du coefficient de dissociation, nous avons tout ce qu'il faut pour calculer cette constante : on trouve un pK_A = - log K_A = 4.92 (alors que pK_{A théo} = 4.75)

Détermination d'un produit de solubilité par conductimétrie :

Merci à chimix.com

• Préparons une solution saturée de chlorure d'argent Ag⁺_(aq) + Cl^-_(aq) en mettant en solution de l'eau un peu de chlorure d'argent solide (poudre blanche).
  
  Ce solide étant peu soluble dans l'eau, il en faut une petite quantité pour arriver à saturer la solution.
• A l'aide d'un conductimètre on relève la conductivité de la solution, on trouve σ = 1.84*10^-4 S.m^-1.
  Pour davantage de précision, on tiendra compte de la conductivité de l'eau pure : σ₀ = 5.48*10^-6 S.m^-1.
• On sait que la conductivité de la solution saturée de chlorure d'argent provient de la dissolution du précipité AgCl_(s) :
  
  
  et donc Ks = [Ag⁺] * [Cl^-] = s * s = s²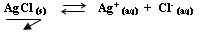
• Aussi on a : σ - σ₀ = λ(Ag⁺) * [Ag⁺] + λ(Cl^-) * [Cl^-] = s * (λ(Ag⁺) + λ(Cl^-))
• Donc : s = (σ - σ₀) / (λ(Ag⁺) + λ(Cl^-))
  
  Sachant que λ(Ag⁺) = 6.19*10^-3 S.m².mol^-1 et λ(Cl^-) = 7.63*10^-3 S.m².mol^-1
  
  s = (1.84*10^-4 - 5.48*10^-6) / (6.19*10^-3 + 7.63*10^-3)
  = 1.29*10^-2 mol.m³
  = 1.29*10^-5 mol/L

(attention à la conversion, il faut repasser en mol/L)

• Enfin Ks = s² = (1.29*10^-5)² = 1.66*10^-10
  d'où pKs = - log Ks = 9.78 (pKs_théo = 9.75)

Constante de dissociation d'un complexe :

Merci au cours d'oxydoréduction de T.Briere

Pour déterminer celle-ci nous allons faire de l'électrochimie (potentiométrie) et passer par la relation de Nernst.

Schéma du montage :

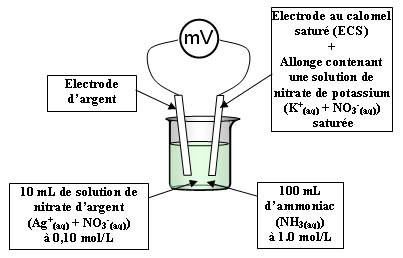
Electrode au calomel saturée :

Elle est constituée de mercure Hg, de calomel Hg₂Cl₂ et d'une solution de chlorure de potassium (K⁺_(aq) + Cl^-_(aq)) généralement saturée.

Cette électrode est une électrode de référence dont le potentiel est connu (à 25°C, E_ECS = 0.25 V par rapport à l'électrode normale à hydrogène (E = 0 V)).

L'allonge remplie de nitrate de potassium saturée permet d'éviter le contact entre les ions chlorure Cl^-_(aq) de l'électrode au calomel saturée et les ions argent Ag⁺_(aq) de la solution dans le bécher.

Sans cette allonge, il y aurait précipitation de AgCl qui fausserait notre détermination de pK_D.

Résultat de l'expérience :

Le millivoltmètre nous donne ΔE = - 0.019 V et on connaît le potentiel normal du couple Ag⁺ / Ag : E⁰(Ag⁺/ag) = 0.80 V.

Calcul de [Ag⁺] en fin de réaction :

On a ΔE = E_Ag - E_ECS d'où E_Ag = ΔE + E_ECS = - 0.019 + 0.25 = 0.23 V

Or E_Ag = E⁰(Ag⁺/Ag) + 0.06 log [Ag⁺]
(relation de Nernst concernant le couple Ag⁺/Ag)

donc :

[Ag⁺] = 10^{(E_Ag - E0(Ag+/Ag))/0.06} = 3.2*10^-10

Cette concentration est très faible, on considère que tout l'argent présent est sous la forme du complexe en Ag(NH₃)₂⁺.
On considère la réaction comme totale.

Equation et tableau d'évolution :

Détermination de pK_D :

Nous pouvons calculer les deux concentrations qui nous manquent :

[NH₃] = n / V_total = 1.0*10^-1 / 110*10^-3 = 9.1*10^-1
[Ag(NH₃)₂⁺] = n / V_total = 1.0*10^-3 / 110*10^-3 = 9.1*10^-3

Puis K_D constante de dissociation du complexe :

K_D = ([Ag⁺] * [NH₃]²) / [Ag(NH₃)₂⁺]
K_D = (3.2*10^-10 * (9.1*10^-1)²) / 9.1*10^-3
K_D = 2.9*10^-8

d'où pK_D = - log K_D = 7.5 (pK_{D théo} = 7.2)

Influence de différents facteurs sur les équilibres :

La température :

Expérience :

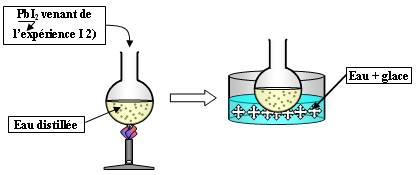
• Le chauffage dissous le précipité de PbI₂.
• Le refroidissement dans la glace le fait re-précipiter.

Compétition entre équilibre :

Expérience :

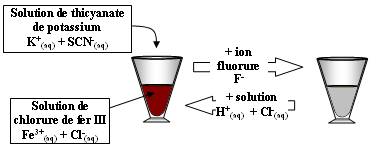
Equation de la réaction de complexation initiale :

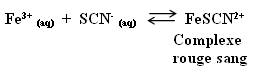
• Lorsque l'on ajoute l'ion fluorure F^-_(aq), il y a destruction du complexe et le contenu du verre à pied devient incolore.
  La réaction est la suivante :

Fe(SCN)²⁺ + F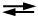^- FeF²⁺ + SCN^-

• Lorsque l'on ajoute une solution d'acide chlorhydrique, il y a re-formation du complexe rouge sang car on libère Fe³⁺ :

F^- + H₃O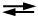⁺ HF + H₂O

Conclusion :

Nous venons d'explorer expérimentalement quelques facettes des équilibres en phase aqueuse ainsi que quelques facteurs pouvant les influencer.
Cette notion d'équilibre chimique est universelle, issue de la thermodynamique, et elle est très utilisée dans l'industrie comme au laboratoire, et pas uniquement en phase aqueuse :
Par exemple en métallurgie avec la réduction des oxydes de fer par le carbone.
On l'utilise aussi dans la vie courante : aspirine tamponnée, protection électrochimique, adoucisseur d'eau.