Agrégation/Capes > Capes : montages de physique > capes-physique-montage-5-interferences
CAPES-Montage physique n°6 :
Expériences portant sur l'acoustique, applications
Pour rechercher un mot dans la page, utilisez la fonction de votre navigateur
(Ctrl + F)
Introduction :
* Un son est généré par une onde de pression (succession de surpression-depression des tranches d'air) qui se propage dans les milieux élastiques :
Ce sont des ondes longitudinales, la propagation se fait dans le sens de la déformation.
* Au VIème siècle avant JC, Pythagore découvre la relation entre la hauteur d'un son et la longueur de la corde qui l'émet.
En 1686, Newton explique la formation et la propagation d'un son.
En 1877 : le premier son est enregistré par Edison.
Le son, nécessité d'un milieu matériel, cavité résonnante :
Le diapason :
Expérience 1 :
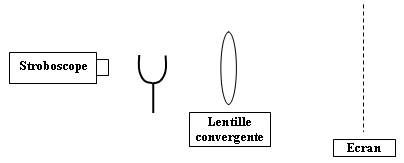
Allumer le stroboscope à sa fréquence minimale, puis augmenter progressivement celle-ci pour trouver la fréquence d'oscillation du diapason (ses branches paraîtront immobiles à l'écran).
En se décalant un peu de cette fréquence, on voit les deux verges du diapason oscillées.
Attention : Le stroboscope donne une indication en nombre de coups par minute, alors que la fréquence est définie par le nombre de coups par seconde.
Pour entendre le son délivré par le diapason, on le relie généralement à une cavité résonnante, c'est la queue du diapason qui viendra faire vibrer l'air dans la cavité.
Cavité résonnante :
Cette cavité sert d'adaptateur d'impédance, elle va permettre de générer des ondes stationnaires.
Il faut impérativement que la longueur de la cavité soit adaptée au diapason qu'elle va recevoir :
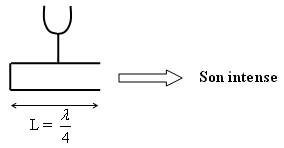
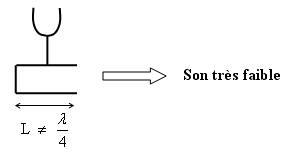
En effet, dans les tuyaux ouverts à une extrémité et fermés à l'autre, la courbe de différence de pression a cette forme :
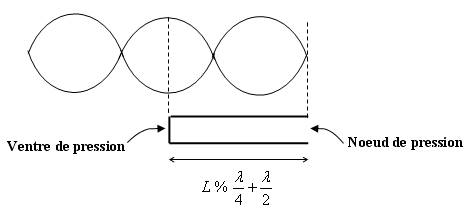
Entre deux maxima ou entre deux minima, on a λ/2.
Phénomène de propagation :
a. Propagation entre deux cavités résonnantes :
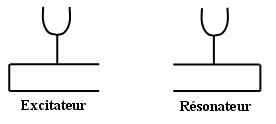
Le diapason et la cavité sont identiques pour l'excitateur et le résonateur
L'excitation de l'excitateur, par percussion à l'aide d'un marteau, produit un son qui fait résonner le résonateur à sa fréquence propre. En effet, si après percution on stoppe l'oscillation des deux verges de l'excitateur, on entend toujours le son.
Même si on éloigne l'excitateur et le résonateur en les mettant aux extrémités de la salle, l'observation restera identique.
b. Propagation par un autre matériau :
Excitons le diapason à l'aide d'un marteau, et mettons sa queue en contact avec une table en bois. Le son se fait alors entendre bien plus distinctement que si la queue du diapason est libre.
En fait, les vibrations du diapason sont transmises à la table puis, sa surface communique une onde de pression à une grande surface d'air : le son est donc plus intense.
Mesure de la vitesse du son : le tube de Kundt :
Présentation du dispositif :
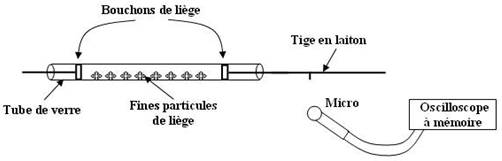
Mesure de la vitesse du son dans l'air :
On frotte la tige de laiton avec un papier absorbant imbibé d'alcool.
La succession des phases de frottements et de glissements sur la tige entraîne la formation d'une vibration au sein du matériau.
Cette vibration est transmise par le bouchon de liège à l'air contenu dans le tube de verre (cavité résonnante).
Si la longueur de ce tube est bien adaptée (on ajuste celle-ci avec le bouchon de liège à gauche), il se forme des ondes stationnaires caractérisées par la formation de petits tas de lièges : ces tas représentent les minima de pression :
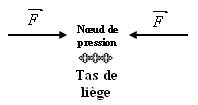
Observation dans le tube de kundt :
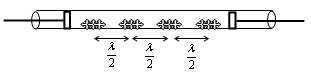
Pour la mesure, on procède alors comme suit :
- On mesure la distance entre les tas de liège : 5 tas = 23.5 cm.
- Or, la distance entre chaque tas représente λ/2. Donc ici sur 5 tas, on a 4 interdistances donc 4*λ/2 = 2 λ = 23.5 d'où λ = 11.7 cm
- A l'aide de l'oscilloscope à mémoire et du micro, on mesure la fréquence de la vibration enregistrée : f = 2940 Hz (ce qui correspond à la fréquence propre de vibration de la tige).
- On finalise alors le calcul en sachant que v (vitesse du son dan l'air) est définie
par : v = λ*f
On trouve v = 344 m/s, on pourrait comparer cette valeur avec la valeur théorique sachant que cette dernière dépend de la température de l'air.
Mesure de la vitesse du son dans le laiton :
La vibration créée par frottements-glissement sur le laiton s'est propagée dans celui-ci.
On connaît la longueur de la tige et d'après sa configuration (deux extrémités libres), on en déduit qu'une longueur de tige correspond à λ/2.
- Or on sait que la tige résonne à la fréquence f = 2940 Hz.
- On calcule la longueur d'onde de la vibration dans le laiton : λ/2 = Ltige = 60 cm d'où λ = 1.20 m.
- On en déduit la vitesse du son dans le laiton comme précédemment :
v = λ*f
On trouve v = 3.53*103 m/s. La valeur théorique étant de 3480 m/s, notre mesure est acceptable.
Remarque :
Le son se propopage bien plus rapidement dans les métaux que dans l'air. C'est ainsi que les indiens collaient leur oreille au rail des chemins de fer afin de détecter l'arrivée d'un train, plutôt que d'essayer d'entendre le bruit dans l'air de celui-ci.
Les ultrasons : propriétés :
Ils correspondent à tous les sons hautes fréquences inaudibles par l'oreille humaine (f > 15 kHz).
Directivité :
On étudie celle-ci à l'aide du dispositif suivant :
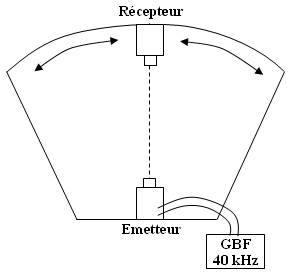
L'émission des ultrasons est très directive contrairement aux basses fréquences où l'émission est quasi isotrope.
C'est en partie pour cela qu'on utilise ces ultrasons dans les techniques de sonar (voir plus loin).
Remarque :
Ainsi les petits haut-parleurs sont plus directifs que les haut-parleurs diffusant les basses fréquences.
Réflexion :
Voici le dispositif utilisé :
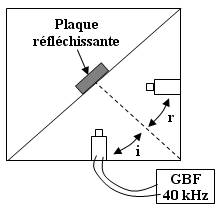
- Si on place l'émetteur et le détecteur normale à la plaque réfléchissante, la réflexion est quasi totale (pas d'absorption par la plaque).
- Si on place l'émetteur et le récepteur avec le même angle par rapport à la normale à la plaque, la réflexion est très bonne, le signal reçu par le détecteur n'est que peu atténué par rapport à celui émis.
Application : le sonar :
On utilise les propriétés de directivité et de réflexion des ultrasons dans cet appareil :
- Un signal ultrasonore est envoyé sur un obstacle, on mesure alors le temps entre l'émission, et la réception du signal réfléchi (de l'écho).
- En connaissant la vitesse de propagation des ondes sonores dans le milieu considéré, on détermine la distance à laquelle était situé l'obstacle :
v = 2*d/t d'où d = (v*t)/2 - La directivité du signal permet une moins grande dispersion du signal émis et de son écho d'où un signal réfléchi plus intense et donc plus facile à détecter.
Diffraction :
Dispositif :
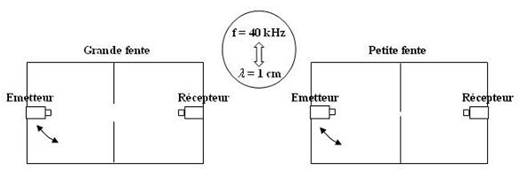
| Si on déplace l'émetteur selon la double flèche, il y a une grosse atténuation du signal reçu par le récepteur. | Un déplacement de l'émetteur engendre une atténuation beaucoup plus faible que le montage avec la grande fente. |
Conclusion :
- Pour qu'il y ait diffraction, il faut que la dimension de l'obstacle diffractant soit de l'ordre de la longueur d'onde du signal à diffracter.
- Plus l'obstacle est petit, plus il y aura diffraction.
Remarques :
- La diffraction intervient dans la taille des haut-parleurs, les gros diffusent des basses fréquences alors que les petits diffusent des hautes fréquences.
- On peut faire l'observation de cette diffraction lorqsue l'on entend une conversation à travers une porte. En effet, que la porte soit grande ouverte, ou simplement entrouverte, l'intensité sonore et pratiquement identique (fvoix = qq 102 Hz équivaut à λ = 0.5 m).
IV Analyse d'un son :
a. Relation hauteur du son perçu-fréquence :
On alimente un haut-parleur par un GBF et on montre que plus la fréquence est haute, plus le son est aigu.
b. Le timbre d'un son :
Il dépend directement du spectre en série de Fourier du signal.
- Sinusoïdale : spectre :
Le son est pur : on obtient le pic de la fréquence fondamentale.
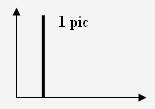
- Triangulaire : spectre :
On observe le fondamental plus quelques harmoniques.

- Carré : spectre :
Présence du fondamental plus beaucoup d'harmoniques.
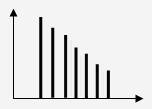
La perception du son change avec la forme du signal c'est à dire avec la présence d'harmoniques et leur nombre en plus du fondamental.
Le fondamental est la fréquence la plus basse du signal.
Les harmoniques se sont d'autres fréquences en plus du fondamental qui sont ajoutées avec plus ou moins d'amplitudes.
Remarque :
La décomposition en série de Fourier du signal de notre voix constitue une empreinte vocale aussi fiable que nos empreintes digitales.
c. Niveau acoustique :

L : niveau acoustique en décibels (dB)
P : puissance de la source en watts (W)
r : distance source-auditeur en mètre (m)
I0 : seuil normal de sensibilité de l'oreille I0 = 10-12 W.m-2
- L varie de 0 (seuil d'audibilité) à 134 dB (seuil de douleur) pour l'oreille humaine.
- Si on augmente la puissance d'une source par deux, son niveau acoustique augmente de 3 dB.
- Si la distance source-auditeur augmente telle que r2 = r1*21/2, le niveau acoustique diminue de 3 dB.
Conclusion :
Nous sommes constamment baignés dans une "ambiance" sonore, il est important de comprendre comment cela fonctionne.
De plus, l'emploi des ultrasons a permis de nombreuses avancées : dans la médecine (échographie) ou la pêche (repérage des bans de poisson par sonar) par exemple.


