Questionnaire TS-Physique-chap 4 :
Décroissance radioactive

Un peu d'histoire :

• Qui a découvert l'existence des rayons X ? En quelle année ?
  
• Un français se base sur les découvertes de son prédécesseur et on lui attribue la découverte de la radioactivité de l'uranium. De qui s'agit-il ?
  
• Quel couple de physiciens célèbres a qualifié les éléments polonium et radium de radioactifs pour la première fois ?
  

Rappels sur l'atome et surtout son noyau :

Nous savons que l'atome est composé d'un noyau et d'un cortège électronique qui l'entoure. Nous allons nous intéresser surtout au noyau.

Complétez :

• Un noyau est composé de ..................., qui rassemblent les ................. et les ........................
  
• En raison de la charge électrique .................. des ..................., le noyau devrait ...................., mais sa ...................... est maintenue par l’..................... .................
  
• La représentation symbolique du noyau d’un atome est la suivante :
  
  où A est le nombre de ..................... autrement appelé nombre de ................
  où Z est le nombre de ..................... autrement appelé nombre de ................ ou encore ................ ......................
• Exemple : le noyau 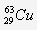est un noyau de ................... qui possède ...... ................ et ................. ...................
  
• Des noyaux qui ont même ............... ....................... mais des nombres de ....................... différents s’appellent des .................... (ils ont donc même nombre de .................. mais un nombre de ...................... différent).
  
• Exemples :
  Pour l’élément uranium, il existe plusieurs isotopes dont ceux-ci :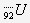 et
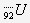
  Pour l’élément carbone, il existe plusieurs isotopes dont ceux-ci :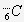 et
  

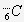
Stabilité et instabilité du noyau :

Malgré l’interaction forte, sur les 1500 noyaux connus (naturels et artificiels), seuls 260 sont stables. Les autres se désintègrent spontanément, plus ou mois rapidement selon leur composition.

• Pour localiser les différents types de noyaux, on utilise un diagramme (N, Z) appelé également diagramme de Segré dont voici ci-dessous l'aspect (vous trouverez une animation intéressante à cette adresse).

  Complétez le nom des axes :

  

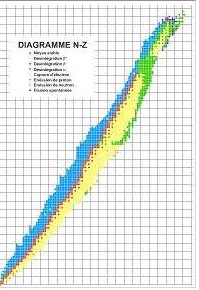
• Complétez :

  • On voit que pour Z<20, les noyaux stables sont ceux notés en ..............., ils se situe sur la ..................., appelée vallée de ........................ (les noyaux ont autant de .................. que de ....................).
    
  • Ensuite, la stabilité du noyau n’est assurée que si le nombre de ......................... est supérieur au nombre de ...................... (si Z est trop élevé, les forces ................................. l’emportent sur les forces ....................... et les noyaux se ........................).
    
  • Aucun noyau dont Z>83 est ...........................
    
  • En bleu sont notés les noyaux qui se désintègrent par la radioactivité ........
    
  • En jaune sont notés les noyaux qui se désintègrent par la radioactivité .........
    
  • En vert sont notés les noyaux qui se désintègrent par la radioactivité ..........
    

La radioactivité :

Définition :

Complétez :

• En dehors de la vallée de ................, les noyaux ................... sont dits .........................
  Chaque noyau va se transformer en noyau ................ en une ou plusieurs ........................... ........................
  Au cours de ce processus, il y aura émission de ....................... qui pourra être accompagné de rayonnement .....................................

Lois de conservation ou lois de Soddy :

Complétez :

• Lors d'une réaction nucléaire, où on ne considèrera que les noyaux des atomes, il y a conservation du nombre de ....................... ......... et du nombre de ......................... ..........
  
• Soit une réaction nucléaire où un noyau père (X) donne naissance à un noyau fils (Y) en émettant une particule chargée P :
  
  
  Ecrivez les équations traduisant les lois de conservation.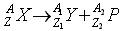
  

Radioactivité α :

• Quel type de noyaux est concerné par cette radioactivité ? Quel type de particule est expulsée ?
  

• Complétez l'équation ci-dessous :

  
  
  
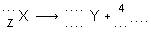
• Le noyau de polonium (A = 210, Z = 84) est radioactif α. Trouvez la nature de son noyau fils et écrivez son équation de désintégration :
  



• Complétez les propriétés de la radioactivté α :

  Les particules α sont arrêtées par une feuille de papier ou une petite couche d’air. Elles sont donc très peu .......................... mais très ......................, c’est à dire dangereuses lorsqu’elles sont ingérées par exemple.

Radioactivité β^- :

• Quel type de noyaux est concerné par cette radioactivité ? Quel type de particule est expulsée ?
  

• Complétez l'équation ci-dessous :

  

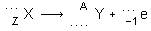
• Remarque importante :

  • L’électron ne provient pas du cortège électronique puisque nous sommes à l’intérieur du noyau.
  • Et comme le noyau ne comporte pas d’électrons, cela signifie que l'électron a été créé.
  • En effet, lors de la radioactivité β^-, le nombre de masse reste constant alors que le numéro atomique augmente d’une unité :
    Ceci ne peut être réalisé que si un neutron s’est transformé en proton.
    Pendant cette transformation, un électron est crée puis éjecté.
• Le noyau de Cobalt (A = 60, Z = 27) est radioactif β^-. Trouvez la nature de son noyau fils et écrivez son équation de désintégration :
  



• Complétez les propriétés de la radioactivté β^- :

  Ce rayonnement β^- est assez ..................... mais est ....................... par une épaisseur de quelques mm d’aluminium.

Radioactivité β⁺ :

• Quel type de noyaux est concerné par cette radioactivité ? Quel type de particule est expulsée ?
  

• Complétez l'équation ci-dessous :

  

• Remarque :

  Le positon n'est pas une particule constituant l'atome (elle est ni dans son noyau, ni dans son cortège électronique), elle est donc forcément créée lors de la transformation d'un proton en neutron.
  
• Le phosphore (A = 30, Z = 15) est un noyau radioactif β⁺ qui a été créé par Irène et Frédérique Joliot-Curie en 1934.
  Trouvez la nature de son noyau fils et écrivez son équation de désintégration :
  



• Complétez les propriétés de la radioactivté β⁺ :

  Les particules β⁺ont une durée de vie très ............... car lorsqu'un positon rencontre un ......................., les deux particules s'annihilent pour donner une émission γ (gamma).
  Cette durée de vie leur permet d'être utilisées en médecine.

Désexcitation γ (gamma) :

• Mis à part le cas de l'annihilation vu ci-dessus, dans quels cas observe-t-on cette désexcitation ? A la suite de quoi ?
  


• Quelle équation écrit-on lorsque l'on veut spécifier qu'un noyau fils se désintègre ?
  
• Quelle est la nature du rayonnement γ ?
  

• Quelles sont ses propriétés ? complétez :

  Du fait de leur énergie, ces photons γ sont très ........................., il faut une grande .................... de ................. pour les arrêter.

Loi de décroissance radioactive :

Etablissement de la loi :

Le but est de trouver la loi mathématique qui régit l'évolution de la population d'un ensemble de noyaux radioactifs. On sait que celle-ci diminue puisque les noyaux se désintègrent.
On utilisera les notations suivantes :
* N₀, le nombre de noyaux radioactifs à l’instant t = 0
* N(t), le nombre de noyaux radioactifs restants à l’instant t
* N(t) + ΔN le nombre de noyau restants à la date t + Δt
(avec ΔN<0 puisque N diminue)

• Calculez le nombre de noyaux qui s'est désintégrés entre t et t + Δt :
  



• Nous savons que ce nombre est proportionnel à deux grandeurs. Complétez :

  • - ΔN est proportionnel à ........... c'est à dire au nombre de noyaux ................. à l'instant ...... dans l'échantillon.
    En effet, pendant une même durée, le nombre de .......................... est deux fois plus ......................... si l’échantillon comporte deux fois plus de ....................
  
  
  • - ΔN est proportionnel à ........ c'est à dire la ................ pendant laquelle on compte les désintégrations.
    En effet, pour un même échantillon, le nombre de ................................. est deux fois plus ....................... si la durée de comptage est deux fois plus ....................
  
  
• Ainsi, on peut écrire cette relation de proportionnalité :
  
  


• λ est la constante de ............................... appelée généralement ........................ ........................... Elle dépend de la ................... de l'échantillon étudié.


• Faites une analyse dimensionnelle permettant de connaître la dimension de λ et donc en quelles unités on pourra l'exprimer :
  



• Souvent, on préfère utiliser une autre constante en relation avec λ : donnez son nom et sa relation avec λ :

  On utilise plutôt la constante de temps pour caractériser la radioactivité d'un noyau. On la note τ :
  τ = 1 / λ
  Cette constante a donc la dimension d'un temps et on l'exprime en s, min ou h.

Loi de décroissance exponentielle :

On rappelle que la désintégration des noyaux radioactifs au niveau microscopique est aléatoire, mais au niveau macroscopique, le nombre moyen N de noyaux restants dans l’échantillon suit une loi déterminée.

• Si on part de la relation de proportionnalité établie plus haut, que l'on fait tendre l'intervalle de temps Δt vers 0 et que l'on utilise des outils mathématiques, on arrive à la loi de décroissance exponentielle.
  Donnez sa forme mathématique et sa forme graphique :
  


• Cette décroissance est caractérisée par une grandeur temporelle qui dépend du noyau radioactif étudié. Comme s'appelle cette grandeur ?
  
• Donnez la définition de cette grandeur temporelle, sa notation :
  



• A partir de la définition mathématique de la demi-vie radioactive écrite ci-desssus, trouvez son expression en fonction de la constante radioactive ou de la constante de temps :