TS-Physique-chap 5 :
Noyau, masse et énergie

Equivalence masse-énergie :

Relation d'Einstein :

• Donnez la définition de la relation d'Einstein qui donne l'expression de l'énergie de masse :

  Pour Einstein en 1905, un système au repos possède une énergie due à sa masse, appelée énergie de masse.
  
  Elle est définie par :
  

  

  
  
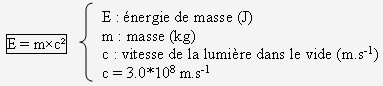
• Ceci à une conséquence très importante quant à la variation de la masse d'un système, laquelle est-ce ?

  La relation d'Einstein implique que quand il y a diminution de la masse d'un système, alors il y a libération d'énergie vers l'extérieur :
  ΔE = Δm * c²

  
  

Défaut de masse et énergie de liaison :

• Donnez la définition littérale et mathématique du défaut de masse :

  La masse d’un noyau est toujours inférieure à la somme des masses des nucléons qui le compose.
  
  Ce défaut de masse est noté Δm et se calcule comme suit pour un noyau (A, Z) :
  Δm = Z * m _P + (A-Z) * m _N - m _NOYAU > 0

  
  
• Donnez la définition littérale et mathématique de l'énergie de liaison d'un noyau :

  L'énergie de liaison correspond à l’énergie qu’il faut fournir à un noyau au repos pour le dissocier en nucléons isolés et immobiles.
  
  Cette énergie de liaison s'exprime en fonction du défaut de masse :
  E_l = Δm * c ²
  Cette énergie est positive puisqu'elle est reçue par le noyau considéré.

  
  
• Exemple : Calculez l'énergie de liaison d'un noyau d'hélium :
  On donne : m _P = 1.67262 * 10 ^-27 ; m _N = 1.67493 * 10 ^-27 ; m _He = 6.64449 * 10 ^-27

  On calcule d'abord le défaut de masse :
  Δm = 2 * m _P + 2 * m _N - m _He = 5.061 * 10 ^-29 kg
  Puis l'énergie de liaison :
  E_l = Δm * c ² = 5.061 * 10 ^-29 * (3.0 * 10 ⁸) ² = 4.6 * 10 ^-12 J
  

  
  

Une nouvelle unité d'énergie : l'électron-volt (eV)

Etant donné la valeur de l'énergie calculée précédemment, on préfère utiliser une nouvelle unité d'énergie, bien plus petite que le Joule.

• Donnez la correspondance entre une énergie en Joule et une énergie exprimée en électron-volt puis calculez l'énergie de liaison du noyau d'hélium en électron-volt :

  On a 1 eV = 1.6 * 10 ^-19 J,
  Donc E _l(He) = 4.6 * 10 ^-12 / 1.6 * 10 ^-19 = 2.8 * 10 ⁷ = 28 MeV.

  
  
• Nous avons utilisé ci-dessus un multiple de l'électron-volt. Donnez les multiples couramment utilisés pour donner des valeurs d'énergie :

  Il y a le KeV : 1 KeV = 10 ³ eV
  Le MeV : 1 MeV = 10 ⁶ eV
  Le GeV : 1 GeV = 10 ⁹ eV

  
  

Energie de liaison par nucléon et courbe d'Aston :

• Donnez la définition de l'énergie de liaison par nucléon :

  Elle est égale à l’énergie de liaison du noyau divisée par le nombre de nucléons présents dans ce noyau : E _l / A.
  Cette énergie de liaison s'exprime généralement en MeV/nucléon.

  
  
• Une fonction mathématique se note généralement y = f(x).
  Dans la courbe d'Aston, qui est y et qui est x ?

  y représente -E _l/A et x représente A.
  La courbe d'Aston est donc la courbe -E _l/A = f(A).

  
  
• Donnez l'allure de la courbe d'Aston :
  
  
  
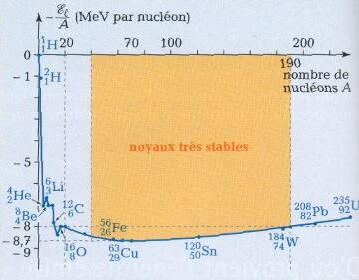
• A quoi sert-elle ?

  Cette courbe permet de comparer la stabilité des différents noyaux atomiques.

  
  
• La courbe d'Aston se lit comme un diagramme énergétique, où se situe donc les noyaux les plus stables ?

  Les noyaux les plus stables se situent dans la partie la plus basse de la courbe d'Aston : moins l'énergie par nucléon des atomes est élevée, plus les noyaux sont stables.

  
  

Réaction de fission et de fusion nucléaire :

Généralités :

• Sur la courbe d'Aston, situez les noyaux qui vont être soumis à la fusion et ceux qui seront soumis à la fission.
  Sur quelle partie de la courbe se trouvent les produits de ces réactions nucléaires ?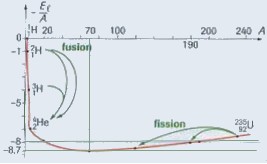
  

  Les noyaux produits par ces deux réactions sont des noyaux plus stables que les noyaux de départ, ils se situent donc dans la partie la plus basse de la courbe d'Aston.
  
  C'est d'ailleurs parce que les noyaux de départ ne sont pas stables, qu'ils participent aux réactions de fission et de fusion ce qui donne des noyaux plus stables.

  
  
• Les réactions nucléaires de fusion et de fission sont qualifiées de réactions provoquées. Qu'est-ce qu'une réaction provoquée ?

  Une réaction nucléaire est provoquée lorsqu’un noyau projectile frappe un noyau cible et donne naissance à deux nouveaux noyaux.

  
  
• A quelles lois doivent forcément répondre les réactions de fusion et de fission étant donné leur caracétère de réaction nucléaire ?

  Les réactions de fusion et de fission doivent vérifier les lois de conservation de Soddy :
  * Conservation du numéro atomique Z
  * Conservation du nombre de masse A

  
  

Réaction de fission nucléaire :

• Définition, complétez :

  Elle se produit lors de la rencontre d’un neutron lent (énergie cinétique Ec = 0.1 MeV), dit neutron thermique, avec un noyau fissile tel l’uranium 235 ; ce qui provoque la naissance de deux noyaux plus légers.
  La première fission de l’uranium 235 a été obtenue par Frédérique et Irène Joliot-Curie
  .
  

• Conditions d'obtention et applications, complétez :

  • Le fait que ce soit un neutron qui initie la réaction est intéressant car il n’y a pas de répulsion lors de la rencontre entre le neutron (non chargé) et le noyau d'uranium.
    
  • Une réaction de fission va donner naissance à des noyaux fils mais aussi à des neutrons, ceux-ci pouvant aller rencontrer d’autres noyaux d’uranium : on obtient alors une réaction en chaîne.
    
  • Il existe deux applications intéressantes de cette réaction :
    * Soit on laisse la réaction nucléaire s'emballer et on obtient une bombe atomique A.
    * Soit on contrôle la réaction pour produire de l'énergie dans les centrales nucléaires.
    
• Exemple de réaction de fission : donnez l'équation de la réaction de fission de l’uranium 235 qui donne naissance à un noyau de strontium 94 et à un noyau de Xénon 140 :
  
  
  

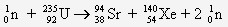
Réaction de fusion nucléaire :

• Définition, complétez :

  Pour avoir une fusion nucléaire, il faut que deux noyaux légers s’unissent pour donner naissance à un noyau plus lourd.
  

• Conditions d'obtention et applications, complétez :

  • Ces noyaux légers sont composés de neutrons et de protons, ainsi, il leur faut une très grande énergie pour vaincre les forces de répulsion : on porte alors le milieu à très haute température. En conséquence, la réaction de fusion est appelée réaction thermonucléaire.
    
  • Ces réactions de fusion se font naturellement dans les étoiles : des noyaux d’hydrogène vont fusionner en plusieurs étapes pour donner des noyaux d’hélium.
    
  • On créé avec cette réaction des bombes thermonucléaires (bombes H). C’est alors la fission nuléaire qui permet d’engendrer la haute température et donc la fusion.
    
  • On cherche depuis des années à contrôler la fusion pour s’en servir dans les réacteurs nucléaires. La difficulté réside dans le confinement du plasma.
    
  • Exemple de réaction de fusion : donnez l'équation de la fusion la plus courante où s'unissent un noyau de deutérium et un noyau de tritium :
    
    
    
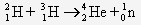
  • Remarque :
    
    * A très haute température, la matière est à l’état de plasma : les électrons se sont dissociés du noyau auquel ils appartenaient, on obtient un gaz d’électrons et de noyaux atomiques.
    
    * Le deutérium et le tritium sont deux isotopes de l’hydrogène, ils ont respectivement un neutron et deux neutrons, alors que le noyau d’hydrogène n’a qu’un proton.
    
  
  

Bilan de masse et d’énergie d’une réaction nucléaire :

Généralités :

• Soit une réaction nucléaire quelconque d’équation :
  
  
  Donner la formule permettant de calculer le bilan énergétique de cette réaction :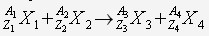

  On utilise la variation de masse entre les produits et les réactifs :
  

  
  Les masses pourront être données en kilogramme ou bien en unité de masse atomique ce qui changera quelque peu la façon de calculer.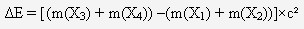
  
  
  

• Remarque :

  En physique nucléaire, on utilise généralement une autre unité de masse que le kilogramme, appelée unité de masse atomique. Elle est définie par : 1 u = 1.66054 * 10^-27 kg et correspond à 1/12^ème de la masse d'un atome de carbone 12.
  

Exemple pour la radioactivité α:

• Ecrivez l’équation de désintégration du radium (Z = 88, A = 226) :
  
  
  
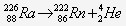
• Calculer en MeV l’énergie libérée lors de la désintégration d’un noyau de radium 226 :
  On donne :
  
  

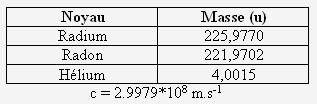
  ΔE = Δm * c²
  = (4.0015 + 221.9702 - 225,9770) * 1.66054 * 10^-27 * (2.9979 * 10⁸)²
  = (4.0015 + 221.9702 - 225,9770) * 931.5 * 10⁶
  = - 4.94 MeV
  
  On rappelle que cette énergie est négative car le système la cède au milieu extérieur.

  
  

• Remarque :

  Les masses seront souvent données en unité de masse atomique, de ce fait on utilisera facilement la formule suivante pour calculer l'énergie libérée par une réaction nucléaire, en MeV :
  
  ΔE (en MeV) = Δm (en u) * 931.5
  
  
• Si on veut comparer l'énergie d'une réaction nucléaire à l'énergie d'une réaction chimique, il faut parler en mole de noyaux.
  
  Quelle est l'énergie libérée par mole de noyaux par la désintégration du radium 226 ?

  On convertit l'énergie obtenue en MeV en Joules :
  Comme 1 eV = 1.6 * 10^-19 J
  alors ΔE = - 4.94 * 10⁶ * 1.6 * 10^-19 = - 7.9 * 10^-13 J
  
  Et comme dans une mole il y a N_A = 6.023 * 10²³ noyaux, l'énergie libérée par mole est égale à :
  ΔE_m = - 7.9 * 10^-13 * 6.02 * 10²³ = - 4.8 * 10¹¹ J.mol^-1

  
  

Exemple pour la radioactivité β:

• Ecrivez l’équation de désintégration du cobalt (Z = 27, A = 60) :
  
  
  
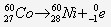
• Calculer en MeV l’énergie libérée lors de la désintégration d’un noyau de cobalt 60 :
  On donne :
  
  

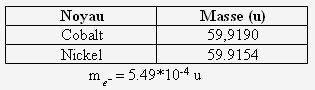
  ΔE (en MeV) = Δm (en u) * 931.5
  = (59.9154 + 5.49 * 10^-4 - 59.9190) * 931.5
  = - 2.84 MeV
  

  
  
• Quelle est l'énergie libérée par mole de noyaux par la désintégration du cobalt 60 ?

  On convertit l'énergie obtenue en MeV en Joules :
  ΔE = - 2.84 * 10⁶ * 1.6 * 10^-19 = - 4.5 * 10^-13 J
  
  Pour l'énergie libérée par mole de noyaux :
  ΔE_m = - 4.5 * 10^-13 * 6.02 * 10²³ = - 2.7 * 10¹¹ J.mol^-1

  
  

Calcul de l'énergie libérée par la fission nucléaire :

• Soit l'équation de fission de l'uranium 235 :
  
  
  Calculez l'énergie libérée par cette fission :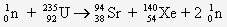
  On donne :
  
  

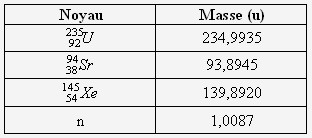
  ΔE (en MeV) = Δm (en u) * 931.5
  = (93,8945 + 139,8920 + 2×1,0087 - 234,9935 - 1.0087) * 931,5
  = - 184,7 MeV

  
  
• Quelle est l'énergie libérée par mole de noyaux par la fission de l'uranium 235 ?

  On convertit l'énergie obtenue en MeV en Joules :
  ΔE = - 184.7 * 10⁶ * 1.6 * 10^-19 = - 3.00 * 10^-11 J
  
  Pour l'énergie libérée par mole de noyaux :
  ΔE_m = - 3.00 * 10^-11 * 6.02 * 10²³ = - 1.81 * 10¹³ J.mol^-1

  
  
• Calculez l'énergie libérée par nucléon pour cette fission :

  Pour réaliser cette fission donc libérer cette énergie, 236 nucléons sont nécessaires, donc :
  ΔE_/nucléon = - 184,7 / 236 = - 0.7826 MeV / nucléon

  
  

Calcul de l'énergie libérée par la fusion nucléaire :

• On considère la réaction de fusion entre un noyau de deutérium et un noyau de tritium :
  
  
  Calculez l'énergie libérée par cette fission :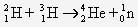
  On donne :
  
  

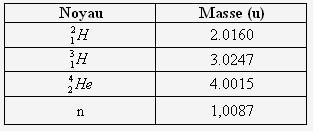
  ΔE (en MeV) = Δm (en u) * 931.5
  = (4.0015 + 1.0087 - 2.0160 - 3.0247) * 931,5
  = - 28.41 MeV

  
  
• Calculez l'énergie libérée par nucléon pour cette fusion :

  Pour réaliser cette fusion donc libérer cette énergie, 5 nucléons sont nécessaires, donc :
  ΔE_/nucléon = - 28.41 / 5 = - 5.682 MeV / nucléon

  
  
• Comparez cette énergie à celle libérée par la fission de l'uranium 235 :

  Par nucléon, la fusion produit bien plus d’énergie que la fission.
  
  De plus, l’approvisionnement en hydrogène (donc en deutérium et tritium puisque ce sont ds isotopes de l'hydrogène et que chaque isotope est abondant d'un certain pourcentage) est facile (eau), et la fusion n’engendre pas de déchets radioactifs (pas de noyaux fils radioactifs à l'issue de la fusion.
  
  Les recherches s’orientent donc vers cette réaction nucléaire, le but étant à terme la production d’énergie dans des centrales.