Bonus

• ➲ Téléchargez l'énoncé du TD au format pdf : Cliquez ici ;
• ➲ Accédez au cours en ligne : Cliquez ici ;
• ➲ Accédez au résumé de cours en ligne : Cliquez ici.

TD EM2 : potentiel et énergie électrostatique

Exercice 1 : potentiel créé par un cercle uniformément chargé

Soit un cerceau de rayon R uniformément chargé portant la densité linéique de charge \(\lambda\) : trouver l’expression du potentiel électrique créé en un point M situé sur l’axe passant par le centre du cerceau.
On prend le potentiel nul à l’infini.

Exercice 2 : potentiel créé par une sphère remplie uniformément chargé

Soit une sphère de rayon R uniformément chargé en volume, la densité volumique de charge est \(\rho\). Le champ créé par celle-ci est donné :

• Si r < R, \(\overrightarrow{E(M)}=\dfrac{\rho r}{3\epsilon_0}\overrightarrow{e_r}\)

• Si r > R, \(\overrightarrow{E(M)}=\dfrac{\rho R^3}{3\epsilon_0r^2}\overrightarrow{e_r}\)

On donne également l’expression du gradient en coordonnées sphériques :

\begin{equation}\overrightarrow{grad} = \dfrac{\partial{}}{\partial{r}} \overrightarrow{e_r}+ \dfrac{1}{r} \dfrac{\partial{}}{\partial{\theta}}\overrightarrow{e_{\theta}} + \dfrac{1}{r \sin \theta} \dfrac{\partial{}}{\partial{\phi}}\overrightarrow{e_{\phi}}\end{equation}

Calculer le potentiel électrostatique créé par cette distribution quelque soit r. On sait que le potentiel est continu partout et que le potentiel à l’infini est pris nul.

Exercice 3 : potentiel créé par deux fils infinis

1. Rappeler l’expression du champ électrique créé par un fil infini portant la densité linéique de charge \(\lambda\) en un point M distant de r de celui-ci.

2. En déduire le potentiel électrostatique créé par ce même fil au point M.

3. On étudie à présent le potentiel créé par deux fils infinis parallèles, l’un portant la densité linéique \(\lambda\), l’autre portant la densité linéique \(-\lambda\). Ces deux fils sont séparés d’un distance 2a.
   Faire un schéma de la situation et exprimer le potentiel en un point M distant de \(r_1\) du premier fil et distant de \(r_2\) du deuxième fil.

4. Déterminer le potentiel \(V_0\) créé au point O situé exactement à mi-distance de chaque fil.

5. Que vaut ce potentiel \(V_0\) si on veut qu’à l’infini, le potentiel créé par cette distribution de deux fils soit nul ?

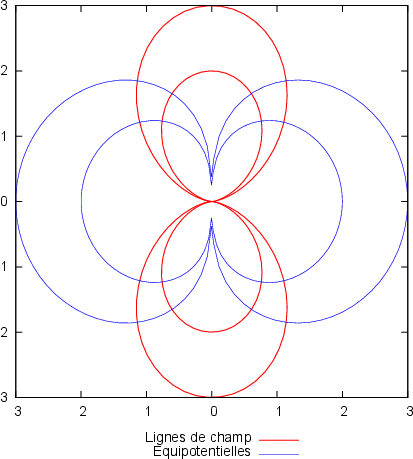
Exercice 4 : lignes de champ et équipotentielles

Soit un champ électrique défini par \(\overrightarrow{E} = \left(\dfrac{2k\cos\theta}{r^3}, \dfrac{k\sin\theta}{r^3},0\right)\) en coordonnées sphériques, k étant une constante.

1. Sachant que le déplacement élémentaire dans ce système de coordonnées s’écrit \(\overrightarrow{dl}(dr,r d\theta,r \sin \theta d\phi)\), trouver l’équation des lignes de champs.
   

   Indications : on rappelle que le champ électrique est en tout point tangent aux lignes de champs et qu’ainsi, on peut écrire \(\overrightarrow{dl}=K \times \overrightarrow{E}\).
   

2. Trouver l’expression du potentiel électrostatique et donnez l’équation des équipotentielles.
   

   Indications :

   • Vous devez obtenir deux équations qui définissent le potentiel.

   • Le potentiel est pris nul là où il n’y a pas de charges (à l’infini).

   • si on intègre une fonction à deux variables ((a,b) par exemple), par rapport à une des variables (a par exemple), la constante d’intégration peut dépendre de b.

3. A l’aide de votre calculatrice, dessiner l’allure des lignes de champ et des équipotentielles. Vérifiez que celles-ci sont bien orthogonales l’une à l’autre en tout point.

Exercice 5 : énergie potentielle d’une distribution de 4 charges identiques

Soit quatre charges q identiques formant un carré de côté 2a. Quelle est l’énergie électrostatique de cette distribution de charge ? On prendra le potentiel nul à l’infini.

Exercice 6 : énergie potentielle d’une molécule

La molécule de dioxyde de carbone \(CO_2\) peut être représentée, de part l’électronégativité des atomes qui la composent, par la succession de charges suivantes : (-q)–(+2q)–(-q). Avec q une charge égale à e/4, on connaît aussi la longueur de la liaison (-q)–(+2q) : d = 116pm.
Trouver l’expression de l’énergie potentielle électrostatique de cette molécule, donner sa valeur en Joule (J) et en électron-volt (eV) et interpréter son signe.

Le potentiel est pris nul à l’infini (*).