Destination prépa > Interaction électrostatique

Destination prépa : 1ère
interaction électrostatique

Définition

Définissons l'interaction électrostatique de la même manière que nous avons défini l'interaction gravitationnelle. En effet l'interaction électrostatique traduit les actions qui s'exerce entre deux corps qui possèdent des charges électriques.

Forces d'interaction entre deux corps chargés : cas attractif

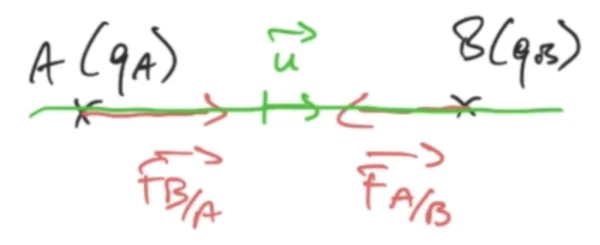
Prenons un corps A qui possède une charge $q_A$, un corps B qui possède une charge $q_B$ , il y a interaction entre ces deux corps c'est à dire que le corps B exerce sur le corps A une force $\overrightarrow{F}_{B/A}$ et le corps A exerce une force sur le corps B $\overrightarrow{F}_{A/B}$ qui est exactement égale et opposée à la force $\overrightarrow{F}_{B/A}$. Au niveau de l'expression littérale, on va pouvoir écrire:

Dans cette expression il nous faut un vecteur unitaire $\overrightarrow{u}$ pour le sens des forces, on doit faire attention à une chose importante : nous avons ici représenté le cas de forces attractives c'est à dire $q_A$ et $q_B$ sont de signes contraires alors dans l'expression de la force ici on a un signe $-$ qui est implicite. Comme la force $\overrightarrow{F}_{B/A}$ doit être dirigée suivant le vecteur $\overrightarrow{u}$ et bien il faut qu'on rajoute un moins et un vecteur $\overrightarrow{u}$ dans l'expression. En effet $\overrightarrow{F}_{B/A}$ a le même sens et la même direction que $\overrightarrow{u}$ mais comme dans l'expression de la force $q_A\,q_B$ est négatif et bien il faut bien rajouter un signe $-$ pour avoir finalement une force $\overrightarrow{F}_{B/A}$ dans le même sens et la même direction que le vecteur $\overrightarrow{u}$.

Les forces s'exprime en newton (N), nous avons les charges qui s'exprime en Coulomb (C) et la distance qui est en mètres (m).

Le facteur $\dfrac{1}{4\,\pi\,\epsilon_0}$ s'appelle la constante de Coulomb, on la note souvent $k$, elle vaut environ $9 \times 10^{9}\,\mathrm{N.m^{2}.C^{-2}}$. La constante de Coulomb fait apparaître $\epsilon_0$ qui est une constante caractéristique du vide : la permittivité électrique du vide.

Forces d'interaction entre deux corps chargés : cas répulsif

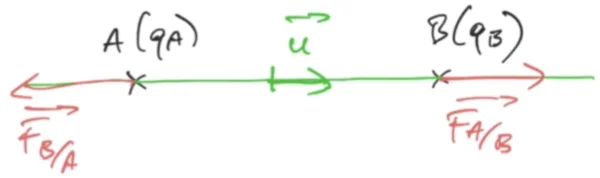
Si maintenant on considère le cas où $q_A$ et $q_B$ sont de même signe, on a un cas répulsif $\overrightarrow{F}_{B/A}$ est dirigé vers la gauche et $\overrightarrow{F}_{A/B}$ est dirigée vers la droite. L'expression mathématiques vectorielle des forces est toujours valable :

Si on prend la force $\overrightarrow{F}_{B/A}$ elle est dirigée suivant le vecteur $-\overrightarrow{u}$ c'est à dire qu'ici nous avons bien le signe moins et le vecteur $\overrightarrow{u}$ et on a bien un produit $q_A$, $q_B$ positif puisque $q_A$ et $q_B$ sont de même signe.

Champs électrostatiques

Dans le même esprit que le champ de gravitation on va pouvoir définir des champs électrostatiques.

Charge positive dans un espace

Par exemple prenons une charge positive dans un espace, elle rayonne tout autour d'elle un champ électrostatique, ce champ à l'aspect suivant :

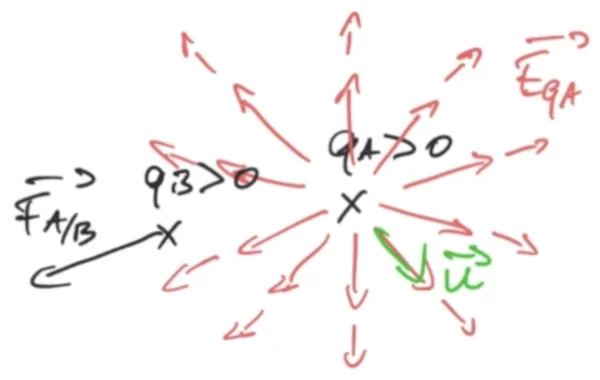
On voit que l'intensité du champ diminue à mesure qu'on s'éloigne de la charge électrique, on notera ce champ $\overrightarrow{E}_{q_A}$. Le champ électrostatique comme le champ de gravitation est invisible, pour le matérialiser il faut qu'en un point M de l'espace en positionne une charge $q_B$ qui va subir une force électrostatique. Si on prend une charge $q_B$ positive, on va avoir une force de répulsion donc la force va être dirigée vers l'extérieur. Au niveau expression mathématique on va pouvoir écrire \begin{equation} \overrightarrow{F}_{A/B} = \dfrac{1}{4\,\pi\,\epsilon_0}\dfrac{q_A\,q_B}{d^2}\,\overrightarrow{u} \end{equation} Eh bien dans cette expression de la force on peut identifier le champ électrostatique créé par la charge $q_a$: \begin{equation} \overrightarrow{E}_{A} = \dfrac{1}{4\,\pi\,\epsilon_0}\dfrac{q_A}{d^2}\,\overrightarrow{u} \end{equation} On a donc \begin{equation} \overrightarrow{F}_{A/B} = q_B\,\overrightarrow{E}_A \end{equation} La charge positionnée en B subit le champ électrostatique créé par A et donc une force électrostatique $\overrightarrow{F}_{A/B}$ qui l'éloigne de la charge en A (car les charges A et B sont de même signe). Si dans cet exemple on avait pris $q_B<0$, la force aurait été dans l'autre sens (attraction) mais l'expression mathématique de la force aurait été la même.

Charge négative dans un espace

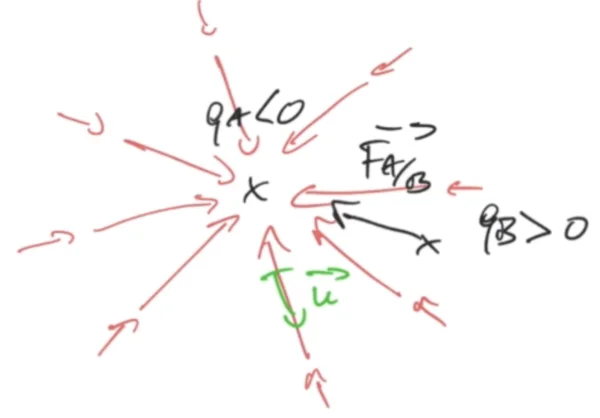
Si on considère le cas de $q_A<0$ on voit que nous avons des lignes de champ qui sont donc des droites qui partent de la charge et qui vont vers l'infini. Ce champ a la particularité d'être dirigé vers la charge alors que pour une charge positive le champ s'échappe de la charge, ici le champ est dirigé vers la charge. Celui-ci existe partout dans l'espace mais il est invisible, on ne pourra le matérialiser que si on place une charge $q_B$, par exemple ici positive, qui va subir une force d'attraction donc $\overrightarrow{F}_{A/B}$ dirigée vers la charge négative. L'expression mathématique que l'on a écrite précédemment est toujours valable on a bien : \begin{equation} \overrightarrow{F}_{A/B} = \dfrac{1}{4\,\pi\,\epsilon_0}\dfrac{q_A\,q_B}{d^2}\,\overrightarrow{u} = q_B\,\overrightarrow{E}_{q_A} \end{equation} ici $q_A$ et $q_B$ sont deux signes contraires donc la force $\overrightarrow{F}_{A/B}$ est à l'opposé du vecteur unitaire $\overrightarrow{u}$. On peut aussi écrire la force de A sur B comme le produit de $q_B$ fois le champ créé par $q_A$. On a $\overrightarrow{E}_{q_A}$ qui est dirigé vers la charge $q_A$ qui est positive, donc la force de A sur B est dans la même direction et le même sens que $\overrightarrow{E}_{q_A}$ c'est à dire dirigée vers la charge. On peut faire le raisonnement similaire si $q_B$ est négative.