Destination prépa > Théorème de l'énergie mécanique
Destination prépa : 1ère
théorème de l'énergie mécanique
Nous avons évoqué précédemment le théorème de l'énergie cinétique très utilisé mais il existe un autre théorème appelé théorème de l'énergie mécanique qui est également essentiel pour traiter les problèmes de mécanique.
Force conservative
Pour utiliser ce théorème, nous allons avoir encore une fois besoin de la notion de travail d'une force et notamment de la notion de force conservative.
Rappelons brièvement ce que nous avons vu sur le travail :
Nous avons ici une force qui s'exerce sur un point M qui se déplace d'un point A à un point B, cette force est constante et son travail de A à B s'écrit : $$W_{\mathrm{AB}}(\overrightarrow{F}) = \overrightarrow{F} \cdot \overrightarrow{\mathrm{AB}}$$ Imaginons maintenant un point C sur notre schéma, nous allons calculer deux fois le travail de la force $\overrightarrow{F}$, une fois entre A et B directement et une fois de A à B mais en passant par le point C.
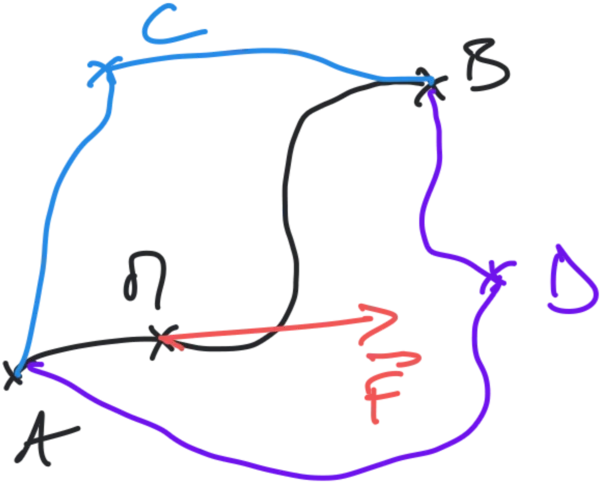
- En allant directement de A à B :
$$W_{\mathrm{AB}}(\overrightarrow{F}) = \overrightarrow{F} \cdot \overrightarrow{\mathrm{AB}}$$
- En allant de A à B en passant par le point C : $$W'_{\mathrm{AB}}(\overrightarrow{F}) = \overrightarrow{F} \cdot \overrightarrow{AC} + \overrightarrow{F} \cdot \overrightarrow{CB}$$
$\overrightarrow{F}$ est une force conservative si ces deux travaux sont égaux. En d'autres termes, on dit que une force est conservative si son travail est indépendant du chemin suivi entre deux points A et B.
Il en est de même si on imagine à un point D, le travail de la force en allant de A à B par le point D sera le même que précédemment si la force $\overrightarrow{F}$ est conservative.
Remarque : nous avons enlevé des hypothèses le fait que $\overrightarrow{F}$ était une force constante, en effet toutes les forces conservatives ne sont pas nécessairement constantes.
Exemples
nous allons pouvoir nous appuyer sur les contenus précédents (théorème de l'énergie mécanique) puisque nous avons déjà vu l'exemple d'une force conservative et l'exemple d'une force non conservative.
Le poids, une force conservative
Le poids est une force conservative car lors du calcul travail du poids, donc $\overrightarrow{P} \cdot \overrightarrow{\mathrm{AB}}$ nous avons montré que celui-ci ne dépendait que du point de départ et du point d'arrivée, ici l'"altitude" sur l'axe O$y$ des points A et des points B.
Ainsi quel que soit le chemin choisi pour calculer le travail du poids entre A et B nous avons le même résultat, le travail du poids ne dépend pas du chemin suivi, le poids est une force conservative
Une force de frottements est une force non conservative
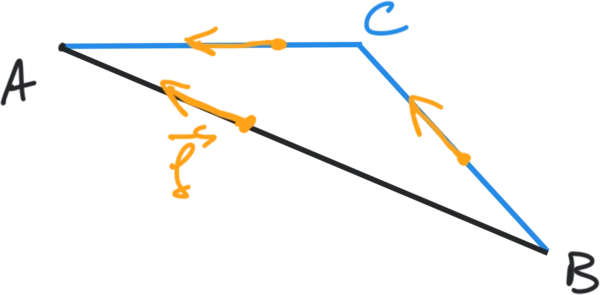
Nous avons aussi rencontré une force non conservative, la force de frottement. En effet si nous regardons le travail de la force de frottement sur le trajet $\mathrm{AB}$ $\overrightarrow{f} \cdot {\mathrm{AB}}$, nous voyons que F et $\mathrm{AB}$ sont colinéaires mais de sens contraire ainsi le travail va s'écrire $- f \times \mathrm{AB}$. On rappelle que cette force F peut être une force de frottement solide ou une force de frottement fluide.

Si maintenant calcule le travail de A à B sur le trajet bleu de la force $\overrightarrow{F}$ et bien maintenant nous avons deux portions de trajet c'est à dire AC + CB le travail va donc s'écrire
$$W_{\mathrm{AB})(\overrightarrow{f})} = \overrightarrow{f} \cdot \overrightarrow{AC} + \overrightarrow{f} \cdot \overrightarrow{CB} = -f \times AC - f \times CB$$
puisque une nouvelle fois la force $\overrightarrow{f}$ est colinéaire de sens inverse au trajet AC et au trajet CB.
On a donc un travail différent sur les deux trajets puisque $\mathrm{AB}$ n'est pas égal à AC + CB.
La distance sur le chemin bleu est plus grande que celle sur le chemin noir, les deux travaux sur deux chemins différents ne sont pas égaux la force de frottement et non conservative.
Le travail de la force de frottement ne dépend pas uniquement des points de départ et d'arrivée mais bien du trajet suivi par le point M lors de son déplacement.
Énergie potentielle
Cette notion de force conservative nous amène à la notion d'énergie potentielle : on pourra définir une énergie potentielle pour chaque force conservative qui s'appliquera sur le système étudié.
Nous avons montré que le travail de la force conservative ne dépend que de l'état du point A et du point B. Alors à ces positions A et B on va associer une nouvelle grandeur physique qui s'appelle l'énergie potentielle, elle définit l'état du système au niveau de A et B.
On peut donc écrire : $$\boxed{W_{\mathrm{AB}}(\overrightarrow{F}_\mathrm{cons}) = E_\mathrm{P}(\mathrm{A}) - E_\mathrm{P}(\mathrm{B})}$$ Cette énergie potentielle s'exprime bien entendu en Joule (J).
Energie potentielle de pesanteur
Pour fixer les idées intéressons nous à l'énergie potentielle associée à la force poids : cette force étant conservative l'énergie potentielle associée s'appelle l'énergie potentielle de pesanteur.
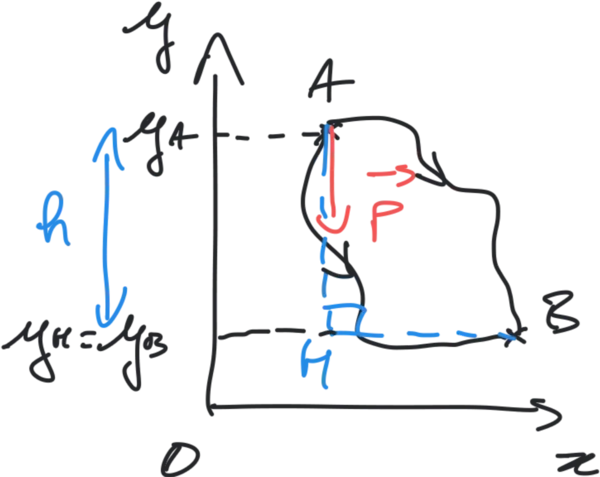
Le travail du poids ne dépend pas du chemin suivi et uniquement des positions de départ et d'arrivée, la force poids est donc conservative et on peut ainsi écrire : $$W_{\mathrm{AB}}(\overrightarrow{P}) = E_{\mathrm{PP}}(A) - E_{\mathrm{PP}}(B) = m\,g\,(y_\mathrm{A} - y_\mathrm{B})$$ En identifiant les deux derniers termes de cette égalité, on peut écrire que $E_{\mathrm{PP}}(A) = m\,g\,y_\mathrm{A}$ et $E_{\mathrm{PP}}(B) = m\,g\,y_\mathrm{B}$.
On comprend alors que l'on peut définir l'énergie potentielle de pesanteur en un point M quelconque :
$$\boxed{E_{\mathrm{PP}}(M) = m\,g\,y_\mathrm{M} + \mathrm{cste}}$$
Nous avons rajouter une constante ici car l'énergie potentielle est en fait définie via une différence (voir ci-dessus), cela signifie qu'en un point l'énergie potentielle de pesanteur est définie à une constante près.
On peut déterminer cette constante en fixant l'origine des énergies potentielles, généralement on prendra $E_{\mathrm{PP}}(y=0) = 0$ c'est à dire une énergie potentielle de pesanteur nulle à une altitude nulle.
Enfin un aspect des choses très important que nous n'avons pas évoqué ici c'est que cette expression de l'énergie potentielle de pesanteur n'est valable que pour un axe O$y$ dirigé verticalement vers le haut.
Si l'axe O$y$ était dirigé vers le bas, nous aurions un moins qui apparaîtrait dans l'expression de l'énergie potentielle de pesanteur. Car pour un trajet $\mathrm{AB}$ il faut que le travail du poids soit positif, c'est-à-dire un travail moteur, et si l'axe est renversé $y_\mathrm{A}$ serait inférieur à $y_\mathrm{B}$ : il faudra prendre des énergies potentielles de pesanteur opposés à celles que nous avions prises.
Énergie mécanique
Si la seule force conservative qui s'exerce sur le système étudié est son poids alors l'énergie mécanique peut être définie comme la somme de l'énergie cinétique et de son énergie potentielle de pesanteur : $$\boxed{E_\mathrm{m} = E_\mathrm{C} + E_{\mathrm{PP}}}$$
S'il y avait plusieurs forces conservatives il faudrait ici ajouter toutes les énergies potentielles pour constituer l'énergie mécanique.
Théorème de l'énergie mécanique
Démontrons le théorème de l'énergie mécanique en partant du théorème de l'énergie cinétique : \begin{align*} \Delta E_\mathrm{c} = E_\mathrm{C}(\mathrm{B})-E_\mathrm{C}(\mathrm{A}) = \sum W_{\mathrm{AB}}(\overrightarrow{F}_\mathrm{ext}) &= W_{\mathrm{AB}}(\overrightarrow{P}) + W_{\mathrm{AB}}(\overrightarrow{F}_\mathrm{non\,conservative}) \\ &= E_{\mathrm{PP}}(\mathrm{A})-E_{\mathrm{PP}}(\mathrm{B}) + W_{\mathrm{AB}}(\overrightarrow{F}_\mathrm{non\,conservative}) \\ \Longrightarrow E_\mathrm{C}(\mathrm{B})-E_\mathrm{C}(\mathrm{A})-E_{\mathrm{PP}}(\mathrm{A})+E_{\mathrm{PP}}(\mathrm{B}) &= W_{\mathrm{AB}}(\overrightarrow{F}_\mathrm{non \,conservative}) \\ \Longrightarrow E_\mathrm{m}(B)-E_\mathrm{m}(A) &= W_{\mathrm{AB}}(\overrightarrow{F}_\mathrm{non\,conservative}) \end{align*} $$\boxed{\Delta E_\mathrm{m} = W_{\mathrm{AB}}(\overrightarrow{F}_\mathrm{non\,conservative})}$$
Cette dernière ligne constitue le théorème de l'énergie mécanique.
Dans les exercices nous rencontrerons deux types d'utilisation du thorème de l'énergie mécanique :
Cas de la conservation de l'énergie mécanique
Le premier cas c'est lorsqu'il n'y a pas de force non conservative appliquée au système, on a alors
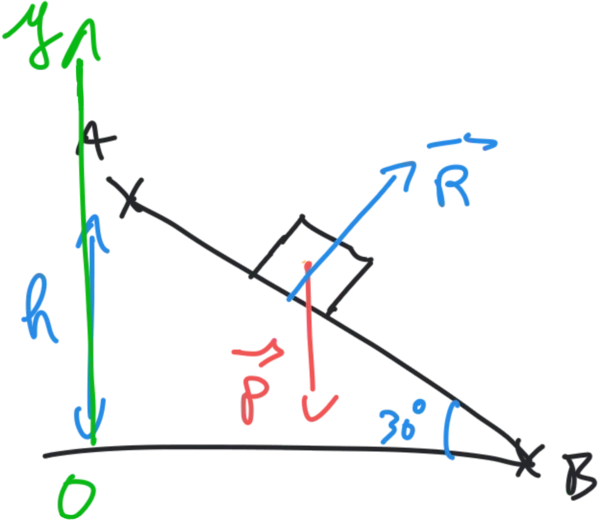
\begin{equation} \Delta E_\mathrm{m} = 0 \Longrightarrow E_\mathrm{m A} = E_\mathrm{m B} \end{equation}Montrons ce cas de conservation de l'énergie mécanique avec le cas classique du solide qui glisse sur le plan incliné :
Nous cherchons la vitesse en B. Le poids est une force conservative alors que la réaction du support ne travaille pas puisque cette force est perpendiculaire au support.
On peut écrire :
\begin{align*} E_\mathrm{m A} &= E_\mathrm{m B} \\ \Longrightarrow \dfrac{1}{2}\,m\,v_\mathrm{A}^2 + m\,g\,y_\mathrm{A} &= \dfrac{1}{2}\,m\,v_\mathrm{B}^2 + m\,g\,y_\mathrm{B} \end{align*}La situation du problème nous dit que $v_A$ est nulle ainsi que $y_\mathrm{B}$.
On obtient alors facilement :
\begin{equation*} v_B = \sqrt{2\,g\,y_A} = \sqrt{2\,g\,h} \end{equation*}On obtient exactement la même formule que pour la vitesse d'un objet qui tombe en chute libre d'une hauteur $h$. Une application numérique avec une hauteur de chute de 100 m nous donne une vitesse de $44{,}7\,\mathrm{m.s^{-1}}$, vitesse assez importante puisque les frottements ont été négligés ici.
Cas de la non conservation de l'énergie mécanique
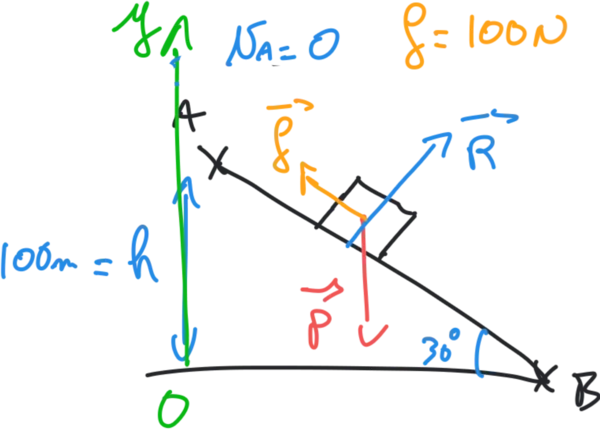
Prenons à présent un cas où il n'y a pas conservation de l'énergie mécanique, reprenons le système que l'on a étudié précédemment et rajoutons une force $f$ de frottement. On va considérer que ça norme est constante égale à 100 N. Nous ne connaissons pas la nature des frottements mais ce n'est pas important ici.
Si on applique le théorème de l'énergie mécanique, la seule force non conservative est la force de frottement que l'on vient d'évoquer et nous n'avons à considérer que l'énergie potentielle de pesanteur puisque seul la force poids dérive d'une énergie potentielle. On rappelle que la force de réaction du support ne travaille pas car elle est perpendiculaire au support à chaque instant.
Nous cherchons toujours la vitesse en B.
\begin{align*} \Delta E_m = \Delta E_C + \Delta E_p &= W_{AB}(\overrightarrow{f}) \\ \Longrightarrow \dfrac{1}{2}\,m\,(v_\mathrm{B}^2-v_\mathrm{A}^2) + m\,g\,(y_\mathrm{B} - y_\mathrm{A}) &= -f \times AB \end{align*}Or on a $\sin\,30 = \dfrac{h}{AB} \Longrightarrow AB = \dfrac{h}{\sin\,30}$ et $y_\mathrm{A} = h$, on obtient :
\begin{align*} v_\mathrm{B} &= \sqrt{\dfrac{m\,g\,h-f \times \dfrac{h}{\sin\,30}}{\frac{1}{2}\,m}} \\ &= \sqrt{2\,g\,h - \dfrac{2\,f\,h}{m\,\sin\,30}} = 38{,}7\,\mathrm{m.s^{-1}} \end{align*}On obtient bien une vitesse moins élevée que celle obtenue sans frottement