Destination prépa > Interaction gravitationnelle

Destination prépa : 1ère
interaction gravitationnelle

Forces entre deux corps massiques

Norme de la force qui s'exerce entre deux corps massiques

Dans cette séquence on parle de l'interaction gravitationnelle : celle-ci représente les actions qui s'exercent entre deux corps qui possèdent une masse.
Prenons l'exemple d'un corps qui possède une masse $m_A$ et qui a à son voisinage une masse $m_B$, il y a interaction gravitationnelle car la masse A exerce une force $F_{A/B}$ sur la masse B et de la même manière le corps B exerce sur le corps A une force $F_{B/A}$.

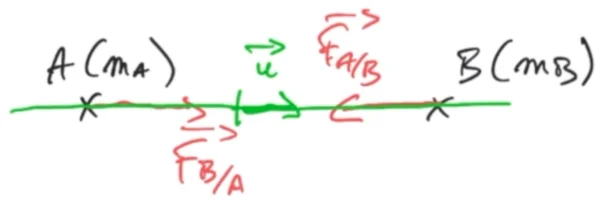
Ces deux forces sont données par l'expression suivante : $$F_{1/2} = F_{2/1} = G\,\dfrac{m_1\,m_2}{d^2}$$

Dans cette expression $G$ est la constante de gravitation, c'est une constante fondamentale de la physique, sa valeur est égale à $6 67 x 10^{-11}$ son unité est un peu compliqué, elle s'exprime en newtons mètres carrés kg moins un ($\mathrm{N.m^2/kg^{-1}}$). En effet, dans cette expression les masses sont en kilogramme (kg) et la distance est en mètres (m), les forces elles sont définies en newton (N). Il y a donc cohérence entre le membre de gauche c'est-à-dire les forces et le membre de droite.

Vecteurs forces

Si l'on souhaite travailler vectoriellement, l'expression mathématique de la force de gravitation, a besoin d'un axe entre A et B que l'on va diriger par un vecteur unitaire c'est-à-dire sa norme qui vaut 1 et qui permet d'avoir juste la direction entre A et B et le sens de A vers B. On va pouvoir écrire ainsi la force $\overrightarrow{F}_{A/B}$ on voit que cette force est opposé aux vecteurs $\overrightarrow{u}$ donc on écrira : $$\overrightarrow{F}_{A/B} = -G\,\dfrac{m_A\,m_B}{d^2}\,\overrightarrow{u}$$ et on a aussi $\overrightarrow{F}_{B/A}$ qui est l'opposé de la force $\overrightarrow{F}_{A/B}$. Si on l'écrit vectoriellement, on a donc: $$\overrightarrow{F}_{B/A} = G\,\dfrac{m_A\,m_B}{d^2}\,\overrightarrow{u}$$ sans le signe moins puisque cette cforce est dans le sens du vecteur unitaire $\overrightarrow{u}$.

Identification entre le poids et la force d'attraction gravitationnelle

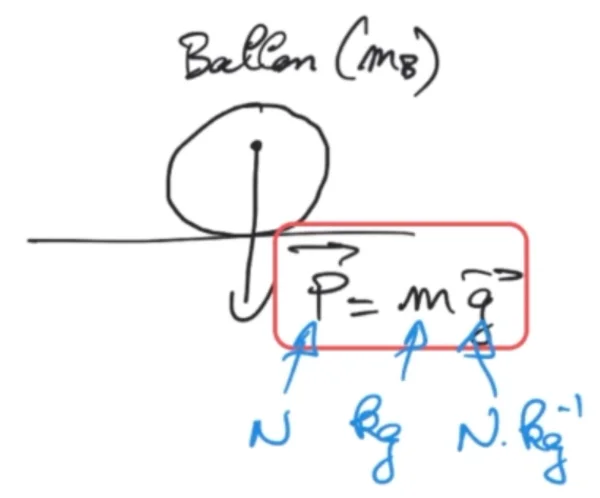
On va maintenant définir le champ de gravitation terrestre. Prenons un objet posé sur le sol terrestre, on sait que celui ci est soumis, entre autres, à son poids $\overrightarrow{P} = m\,\overrightarrow{g}$ avec le poids qui s'exprime en newton (N), la masse en kilogramme (kg) et $\overrightarrow{g}$ l'intensité de la pesanteur ou champ de gravitation terrestre qui s'exprime en newton par kilogramme moins un ($\mathrm{N.kg^{-1}}$).

On sait que ce poids est exactement équivalent à la force qu'exerce la Terre sur l'objet donc ici le ballon. Ecrivons cette égalité en norme, on va pouvoir écrire que : $$m_{\mathrm{ballon}} \times g = G\,\dfrac{m_\mathrm{ballon}\times m_{\mathrm{Terre}}}{R_{T}^2}$$ Nous faisons apparaître ici le rayon terrestre puisque on prend en compte la distance de l'objet au centre de la Terre.

En identifiant ces deux expressions on se rend compte que le petit $g$, le champ de gravitation terrestre, est égale $G\,\dfrac{m_\mathrm{Terre}}{R_T^2}$.
Un petit calcul permet d'avoir la valeur du champ de gravitation terrestre, on obtient 9,81 Newton par kilogramme.

Champ de gravitation terrestre

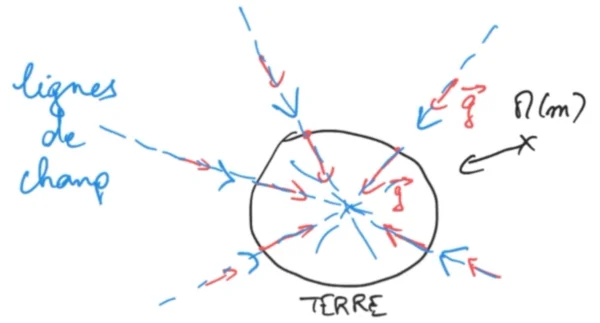
Représentons à présent ce champ au voisinage de la terre on sait que tout objet à la surface de la terre est attiré vers le centre de celle-ci, on va donc pouvoir dessiner les champ de gravitation dirigé vers le centre de la terre. Mais un objet situé dans l'espace va être également attiré vers le centre de la terre mais cette fois ci avec un champ de gravitation plus petit puisque le champ dépend de la distance au centre la Terre au carré. Cette valeur de 9,81 donnée précédemment n'est valable qu'à la surface de la Terre.

Ligne de champ

Si on trace les lignes tangentes au champ dans une direction on voit qu'elles passent toutes par le centre de la Terre et on les appelle des lignes de champ. Elles permettent de connaître la direction et le sens du champ de gravitation tout autour de la Terre. Ces lignes sont orientées par le sens du champ c'est-à-dire ici vers le centre de la Terre, en effet le champ de gravitation est un chant attractif.

Enfin disons un petit mot sur la notion de champ et de force de gravitation : tout autour de la Terre existe ce champ de gravitation terrestre qui dépend donc de la distance au centre de la Terre, il s'agit bien d'un champ vectoriel puisqu'en un point de l'espace nous avons les trois caractéristiques sens, direction et norme. Ce champ est invisible, pour le matérialiser il faut positionner une masse qui va subir à ce moment-là une force de gravitation et donc qui va nous permettre de rendre compte de l'existence du champ de gravitation.