Destination prépa > Forces et mouvement

Destination prépa : 1ère
mouvement et forces

Abordons ici quelques notions essentielles de mécanique.

Tracé d'un vecteur vitesse

nous avons représenté une chronophotographie. Nous avons en effet photographié un objet en déplacement à intervalle de temps régulier. Nous avons donc ici les différentes positions du point M au cours de son mouvement. Généralement, on note les positions de la façon suivante : $\mathrm{M}_1$, $\mathrm{M}_2$, $\mathrm{M}_3$, etc.

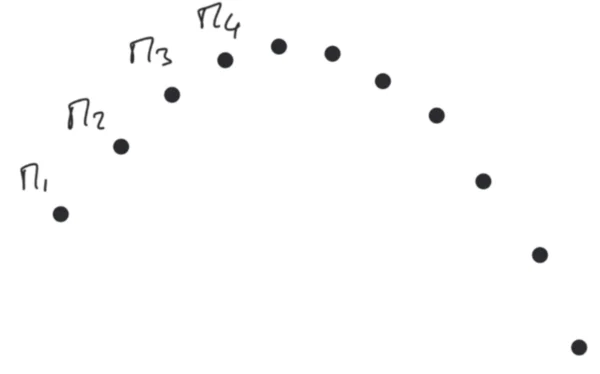
Sur cette chronophotographie, on peut représenter le vecteur vitesse du point M à un instant donné. La meilleure méthode pour cela est d'utiliser la formule suivante $$\overrightarrow{v} = \dfrac{\overrightarrow{\mathrm{M}(t-\Delta t)\,\mathrm{M}(t+\Delta t))}}{2\,\Delta t}$$ où $\Delta t$ est le temps entre deux photographies, c'est-à-dire ici entre deux points M1 et M2 par exemple.

Fixons les idées en calculant un de ces vecteurs un : on veut calculer le vecteur vitesse au point numéro 2. On va donc mesurer la distance $\mathrm{M_1M_3}$, distance entre le point 1 et le point 3 et diviser celle-ci par deux fois Delta t $$\overrightarrow{v_2} = \dfrac{\overrightarrow{\mathrm{M_1M_3}}}{2\,\Delta t}$$

Comment procéder pour tracer ce vecteur vitesse ? On va donc relier les points $\mathrm{M}_1$ et $\mathrm{M}_3$ et mesurer la distance entre ceux-ci, ici, on a environ 4,5 cm. On va donc diviser cette distance de 4,5 cm par 2 fois l'intervalle de temps soit ici, la chronophotographie ayant été faite avec un intervalle de temps de 60 millisecondes entre les images $$v_2 = \dfrac{4,5}{2 \times 0,06} = 37,5\,\mathrm{cm.s^{-1}}$$

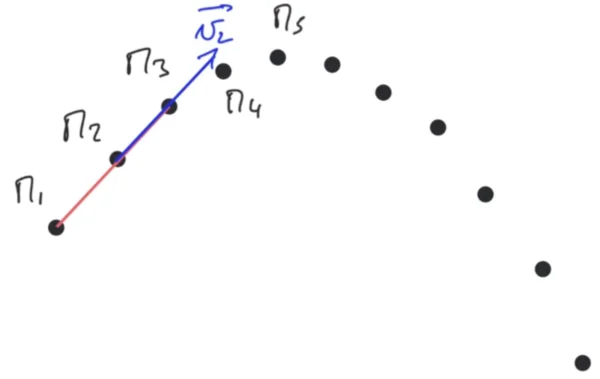
Nous définissons maintenant une échelle de vitesse pour pouvoir dessiner le vecteur vitesse sur la chronophotographie. Ici, on prend $$1\,\mathrm{cm} \rightarrow 0,1\,\mathrm{m.s^{-1}}$$ En effet, si on convertit la vitesse $v_2$ en mètre par seconde, on va avoir $0,375\,\mathrm{m.s^{-1}}$, notre vecteur $v_2$ va donc faire 3,75 cm. Pour tracer ce vecteur, on part du point $\mathrm{M}_2$, on trace le vecteur tangentiel à la droite $\mathrm{M_1M_3}$ de la longueur 3,75 cm dans la direction du mouvement, c'est-à-dire de $\mathrm{M_1}$ à $\mathrm{M_3}$ et on note le vecteur $\overrightarrow{v_2}$.

Tracé d'un vecteur variation de vitesse

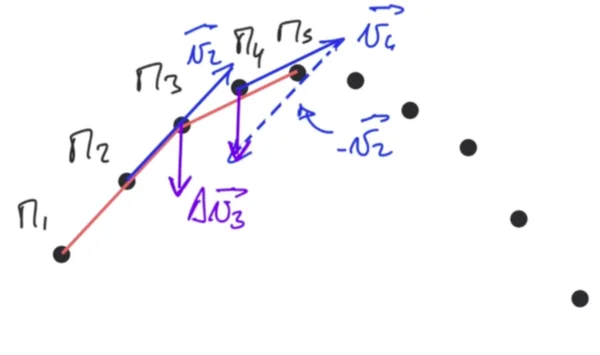
Nous allons maintenant nous intéresser au vecteur variation de vitesse. L'idée est de calculer le vecteur variation de vitesse au niveau du point $\mathrm{M_3}$ sachant que nous avons la vitesse au point $\mathrm{M_2}$, on va calculer la vitesse au point $\mathrm{M_4}$ et on fera la différence entre le vecteur de vitesse $\overrightarrow{v_4}$ et le vecteur de vitesse $\overrightarrow{v_2}$ pour avoir le vecteur appelé $\Delta\overrightarrow{v_3}$.

Pour calculer $\overrightarrow{v_4}$, on fait comme précédemment $$v_4 = \dfrac{\mathrm{M_3M_5}}{2 \times \Delta t}$$ On obtient une vitesse en norme de 27 $\mathrm{cm.s^{-1}}$ que l'on va pouvoir convertir en mètre par seconde pour tracer ce vecteur avec la même échelle que celle utilisée précédemment.

Nous pouvons à présent effectuer la construction vectorielle c'est à dire prendre le vecteur $-\overrightarrow{v_2}$ et venir le positionner au niveau de l'extrémité de $\overrightarrow{v_4}$, le vecteur obtenu $\Delta\overrightarrow{v_3}$ est donc ici entre le point de départ en $\mathrm{M_4}$ et le point d'arrivée de la construction vectorielle. On a pour habitude de mettre ce vecteur au niveau de $\mathrm{M_3}$ puisque ce vecteur c'est bien Delta $\Delta\overrightarrow{v_3}$.
On peut alors, si on le souhaite, mesurer la longueur de ce vecteur pour connaître en valeur la variation de vitesse au point 3.

Résultante des forces

Quand on traite un problème de mécanique on définit tout d'abord le système étudié puis le référentiel dans lequel on va faire l'étude. Ensuite on s'intéresse aux forces extérieures qui s'appliquent sur ce système : en effet ce sont ces forces extérieures qui vont permettre de connaître les changements de mouvement du système.
Ces changements peuvent être un changement de sens, de direction ou bien de vitesse. Par exemple les force de frottements vont modifier la vitesse de notre corps en mouvement ...
On appelle résultante des forces extérieures la somme vectorielle de toutes les forces qui s'exercent sur le système.

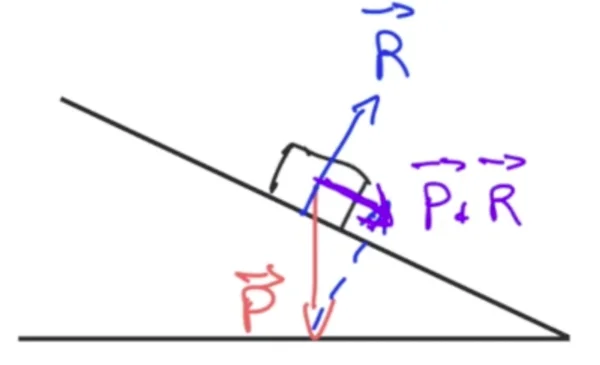
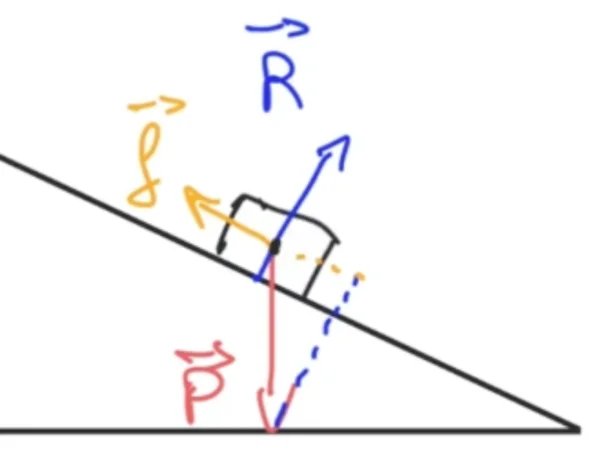
Prenons un exemple classique d'un corps sur un plan incliné, il serait par exemple soumis à son poids et la réaction du support. La résultante des forces est tout simplement la somme vectorielle on vient positionner la réaction du support au niveau de l'extrémité du poids et on obtient ici la résultante des forces $\overrightarrow{P} + \overrightarrow{R}$. Ce vecteur résultant de force va nous donner une indication sur les changements de mouvement du système positionné sur la pente.

On rencontrera parfois un cas où la résultante des forces est nulle. En effet si nous prenons le schéma ici nous voyons qu'une force s'est rajoutée la force $f$ par exemple une force de frottement.

Si nous construisons la somme des forces nous voyons que nous revenons au point initial, c'est à dire que nous partons du centre de gravité nous faisons la somme de $\overrightarrow{P} + \overrightarrow{R} + \overrightarrow{F}$ et revenons au centre de gravité. Ainsi la somme des forces extérieures est égale à $\overrightarrow{0}$, on a donc une résultante de force qui est nulle : on dit que les forces se compensent le mouvement du système étudié ne sera alors pas modifié.

Résultante des forces et variation de mouvement

La résultante des forces va nous permettre de connaître l'évolution du mouvement du système ainsi nous allons voir la relation entre cette résultante et la variation du vecteur vitesse mathématiquement on peut écrire $$ \sum \overrightarrow{F}_\mathrm{ext} = m\,\dfrac{\Delta\overrightarrow{v}}{\Delta t}$$ que la somme des forces extérieures c'est à dire la résultante des forces est égal à petit m la masse du système fois la variation du vecteur vitesse divisée par l'intervalle de temps.
Dans cette expression la résultante des forces s'exprime en Newton (N), la masse en kilmogramme (kg), la variation de vitesse en mètre par seconde ($\mathrm{m.s^{-1}}$) et le temps en seconde (s).

On peut voir que le terme $\dfrac{\Delta \overrightarrow{v}}{\Delta t}$ va s'exprimer en mètre seconde moins deux ($\mathrm{m.s^{-2}}$) : ceci est l'unité d'une accélération ! Nous verrons en effet que cette loi est une forme simplifiée de la deuxième loi Newton qui est vue en terminale.

Que peut-on déduire de cette loi ?

• Premièrement la somme des forces et la variation du vecteur vitesse ont même sens et même direction : ainsi sur la chronophotographie que nous avons étudié dans les diapositives précédentes la direction et le sens du vecteur $\Delta\overrightarrow{v}_3$ nous donnait la direction et le sens de la résultante des forces qui s'appliquaient au système.
  
  
• Dans cette formule on voit également que deux paramètres jouent un rôle essentiel dans la relation entre la somme des forces et la variation du vecteur vitesse, il s'agit de la masse du système ainsi que de l'intervalle de temps. On peut interpréter cela en disant que pour une même résultante des forces et pour un même intervalle de temps la variation de vitesse sera d'autant moins grande que la masse sera importante et inversement.
  Il suffit pour son convaincre d'écrire la formule sous la forme $$\Delta \overrightarrow{v} = \dfrac{\sum \overrightarrow{F}_\mathrm{ext} \times \Delta t}{m}$$ En effet la masse et la grandeur inertielle du système, plus la masse du système est importante plus il a d'inertie cela signifie que :
  • Depuis l'immobilité il est difficile de le mettre en mouvement,
  • Quand il est en mouvement il est difficile de modifier celui-ci

Principe de la simulation numérique

La loi que nous avons vu précédemment écrit sous la forme $\Delta \overrightarrow{v} = \dfrac{\sum \overrightarrow{F}_\mathrm{ext} \times \Delta t}{m}$ va nous permettre de comprendre comment fonctionne une simulation numérique c'est-à-dire le calcul de proche en proche, point par point d'une des caractéristiques du mouvement d'un objet, par exemple ici la vitesse.

Pour cela il faudra connaître un certain nombre de paramètres : ici la somme des forces et la masse, il faut aussi connaître les conditions initiales ici $v(t=0)$.

Enfin nous aurons besoin de choisir un intervalle de temps pour les calculs : ce choix dépend en partie du nombre de points que l'on souhaite avoir sur notre reconstitution du mouvement du point M. Pour l'exemple ici on va prendre un $\Delta t = 0,5\,\mathrm{s}$.

Nous n'allons pas travailler vectoriellement ici mais uniquement en norme pour connaître l'évolution de la vitesse au cours du temps. On va donc commencer par calculer

• $v(t=0,5\,\mathrm{s}) = v(t=0) + \Delta v = v(t=0) + \dfrac{\sum F_\mathrm{ext}\times 0,5}{m}$
  Tous les paramètres sont connus pour calculer cette vitesse.
  
  
• Puis on peut calculer à l'instant suivant, soit à $t = 1\,\mathrm{s}$, par le même processus:
  $v(t=1\,\mathrm{s}) = v(t=0) + \Delta v = v(t=0,5\,\mathrm{s}) + \dfrac{\sum F_\mathrm{ext}\times 0,5}{m}$

Nous allons pouvoir poursuivre le processus pour calculer la vitesse à $t=1,5\,\mathrm{s}$ etc. Le but sera de tracer la courbe de vitesse en fonction du temps pour le mouvement du point M.

Étant donné qu'il y a ici une répétition de calculs similaires, on utilisera plutôt un algorithme, par exemple un algorithme Python, qui permettra de calculer de proche en proche les différentes vitesses en lui donnant au départ les grandeurs connues, les conditions initiales ainsi que l'intervalle de temps que nous aurons choisi.